Значения вероятности для гауссовского распределения при различных

k	1	2	3	4
	0,6827	0,9545	0,9973	0,9999

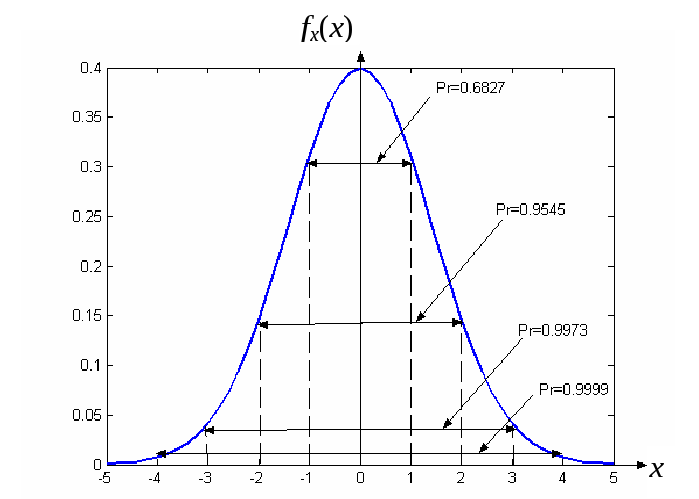
Рис. 2.6. Значения вероятности

для гауссовской с.в. при ,

Из таблицы в частности, следует, что для модуля центрированной гауссовской случайной величины, т.е. , квантиль порядка 0,6827 равен , а вероятность того, что значение центрированной гауссовской случайной величины принадлежит интервалу, равна 0,997. Обычно величину, равную, называютпредельным значением или предельной ошибкой, если случайная величина описывает погрешности тех или иных измерений.

Тот факт, что для гауссовской случайной величины

=0,997, (2.55)

называют правилом трех сигм.

Для гауссовской случайной величины часто используют следующие количественные характеристики.

Среднее абсолютное отклонение, определяемое как математическое ожидание модуля , т.е. [38, c. 578]

. (2.56)

Вероятное отклонение (вероятная ошибка) , которое представляет собой квантиль порядка для, т.е.

=0,5. (2.57)

Иными словами, это такое значение, при котором совпадают вероятности событий и, т.е. это медиана для модуля. Для стандартизованной гауссовской с.в. вероятное отклонение, так что для центрированной случайной величины с дисперсиейимеем [38, c. 578]

. (2.58)

2.5. Другие типы случайных величин

Помимо гауссовских и равномерно распределенных непрерывных случайных величин существуют и другие их типы с различными видами соответствующих им функций плотностей распределения вероятностей.

В частности, можно привести пример положительной случайной величины, имеющей распределение Рэлея, задаваемое в виде

. (2.59)

Плотность распределения., математическое ожидание и дисперсия для случайной величины с таким распределением определяются как:

; (2.60)

;

.

Примеры плотности при разных приведены на рис. 2.7.

Рис. 1.1.7. Графики ф.п.р.в. Рэлея при разных значениях :

=0,5; ; 

Особенность распределения Рэлея заключается в том, что соответствующая ему плотность, в отличие от рассмотренных ранее, не является симметричной относительно математического ожидания.

Плотности распределения часто используемые в прикладных задачах и соответствующие им выражения для вычисления математического ожидания и дисперсии приведены в табл. 2.3 [85, c. 31].

Т а б л и ц а 2.3

Виды функций плотности распределения вероятностей и соответствующие им характеристики

Наименование	Плотность распределения	Математическое ожидание	Дисперсия
Бета (Beta)
Хи – квадрат со степенью свободы (Chisquare)
Экспоненциальное (Exponential)
Гаммма (Gamma)
Нормальное (Normal)
Рэлея (Rayleigh)
Равномерное (Uniform)

П р и м е ч а н и е. ;– гамма-функция;– бета-функция [38].

Выше были рассмотрены случайные величины, при введении которых предполагалось, что в качестве множества элементарных событий выступает все множество или некоторое подмножество действительных чисел. Такие случайные величины получили наименование непрерывных с.в.

Дискретные случайные величины

Для дискретных случайных величин в качестве выборочного пространства выступает конечный или счетный набор чисел.

. Для дискретных случайных величин их статистические свойства полностью определяются набором чисел

,

каждое из которых задает вероятность принятия случайной величиной значения.

Статистические свойства дискретной случайной величины можно адекватно описать с помощью непрерывной случайной величины, плотность распределения которой имеет вид

(2.61)

где - дельта-функция.

С использованием такого представления удается получить ряд соотношений, справедливых для дискретных случайных величин; в частности, выражения для математического ожидания и дисперсии будут иметь вид:

, (2.62)

. (2.63)