Раздел 3. Совокупность случайных величин (случайные векторы).

3.1. Определение случайного вектора и его описание.

Случайным называется вектор, каждая компонента которого является случайной величиной.

Примеры:

1. Точка приземления космического аппарата с двумя случайными координатамии.

2. Успеваемость студента характеризуется совокупностью случайных величин-оценок

3. Состояние технического устройства в момент времени характеризуется системой нескольких случайных величин.

Очевидно, что свойства системы случайных величин не исчерпываются свойствами отдельных величин важны также связи между величинами.

Для случайного вектора его свойства в полном объеме задаютсясовместной функцией. или совместной плотностью распределения, определяемыми в виде:

(3.1)

; (3.2)

. (3.3)

Выражение (3.1) задает вероятность события, при котором для каждой компоненты выполняется неравенство ,

Совместные функция распределения и плотность распределения. так же, как и в одномерном случае обладает свойствами:

1. Функция распределения является не убывающей функцией и, как следствие плотность распределения неотрицательна.

2. Плотностьудовлетворяет условию нормировки, т.е.

. (3.4)

3. Если хотя бы один из аргументов обращается в ,функция распределения равна нулю, например, для двумерного распределения

Это свойство, в частности вытекает из определения функции распределения , т.к. события,, а также их произведениеневозможны.

4. ;

5. Кроме того, совместная плотность распределения. удовлетворяет условиям согласованности, которые при m<n записываются как

, (3.5)

и является симметричной функцией своих аргументов.

Последнее означает, что функция плотности. для вектора не зависит от того, в какой последовательности расположены его компоненты, в частности.

6. Например, для двумерного распределения

, (3.6)

, (3.7)

где ,-функции распределения случайных величинсоответственно

,.

Действительно, т.к. -достоверное событие имеем

.

Зная функцию распределения можно найти вероятность попадания случайной точки в пределы прямоугольника с координатами, при этом вероятность попадания будет определяться выражением

.

Уменьшая , в пределе получим плотность для двумерной функции

.

Элемент вероятности для двумерных случайных величин определяется как

. (3.8)

Выражение плотностей распределения отдельных случайных величин через совместную плотность распределения(двумерный случай) имеют вид

,

,

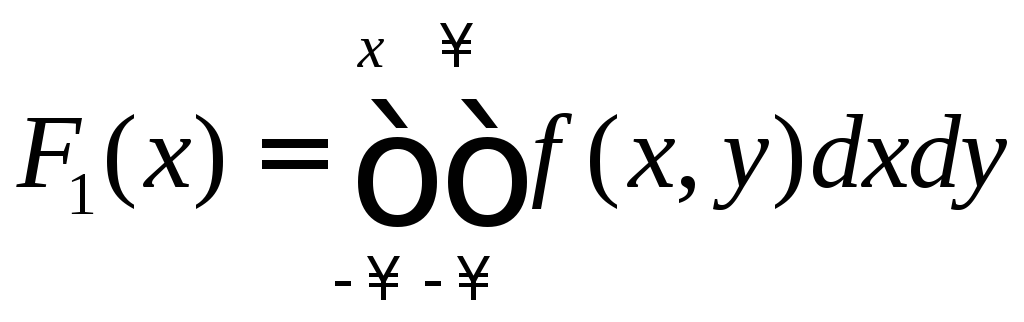или

, .(3.9)

Независимость случайных величин.

Независимость случайных величин можно ввести через независимость событий. Действительно, пусть задана функция распределения

Рассмотрим событияиЕсли эти события независимы, то

т.е. функция распределения совокупности независимых случайных величин равна произведению функций распределения. Если найти вторую производную, представляющую плотность получим

,

Как следствие, можно дать следующее определение:

случайные величины ,называются взаимнонезависимыми, если совместная плотность их распределения равна произведению плотностей для каждой из этих случайных величин., т.е.

. (3.10)

Аналогично вводится определение и для независимых случайных векторов.

Если случайные величины зависимы, то для описания совместного закона распределения нужно знать условный закон распределения одной из них.

Условным законом распределения одной из величин называется закон распределения вычисленный при условии, что другая случайная величина приняла определенное значение( или попала в какой-то интервал)

Для функции распределения имеет место представление

Аналогично

На практике обычно применяют другой вид условного закона

(3.11)

или

Для плотности распределения (теорема умножения плотностей)

, (3.12)

или.

Действительно, рассмотрим элемент вероятности, равный вероятности попадания в элементарный прямоугольник со сторонами.

Попадание в него представим как произведение двух событий

, ,

откуда

Найдем предел при .

Получим.

Откуда.

Из этой формулы имеем

. (3.13)

Аналогично

. (3.14)

Условные плотности распределения обладают свойствами обычных плотностей, а именно

, , (3.15)

, . (3.16)

Пример. Точка изображающая объект на экране локатора распределена с постоянной плотностью в пределах кругарадиусас центром в начале координат. Записать выражение для совместной плотности. Найти плотности,и условные плотности,.

Решение.

Совместная плотность:

Так как следует, что

.

Плотности .

,

.

Условные плотности,.

.

Так както случайные величинызависимы.