Среднеквадратический эллипс ошибок, круговая вероятная ошибка

Проанализируем более подробно характеристики, используемые для описания свойств двухмерных гауссовских векторов. Двухмерный случай весьма важен в задачах обработки статистической информации. Так, при решении навигационных задач на плоскости нередко полагают, что координаты объекта представляют собой гауссовский случайный вектор с математическим ожиданием в точке его предполагаемого местонахождения. Для описания неопределенности расположения точки на плоскости используют введенные выше эллипсы равных вероятностей, в частности эллипс, соответствующий уравнению (3.35) при . Поскольку этот эллипс пересекает оси в точках, совпадающих со значениями соответствующих СКО, т.е. при, а при, он получил наименованиесреднеквадратического эллипса ошибок, или стандартного эллипса [23]. В навигационных приложениях для его описания используют параметры эллипса: большую ималую полуоси и дирекционный угол , задающий ориентацию большой полуоси относительно оси. Эти три параметра полностью определяют матрицу ковариаций двухмерной гауссовской плотности. На рис. 3.4 изображен частный случай, когда, , , и таким образом

, (3.36)

т.е. размеры полуосей эллипса определяют значения СКО по каждой координате.

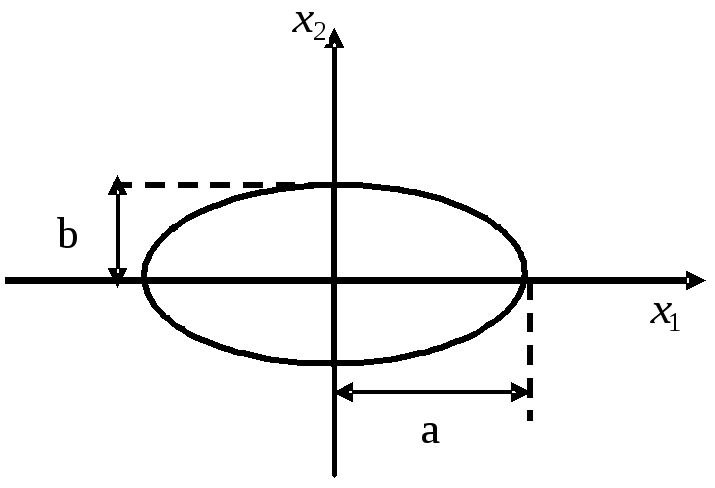
Рис. 1.2.4. Эллипс ошибок для двухмерного гауссовского вектора

с независимыми компонентами

При оценивании точности местоположения подвижных объектов весьма важным представляется умение охарактеризовать неопределенность местоположения одним числом. Для этих целей обычно используют значения вероятности попадания точки на плоскости в ту или иную заданную область . Для двухмерного центрированного гауссовского вектора с плотностью

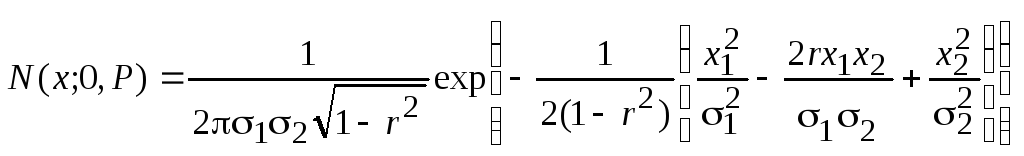
эта вероятность определяется как

, (3.37)

Если в качестве выступает область, ограниченная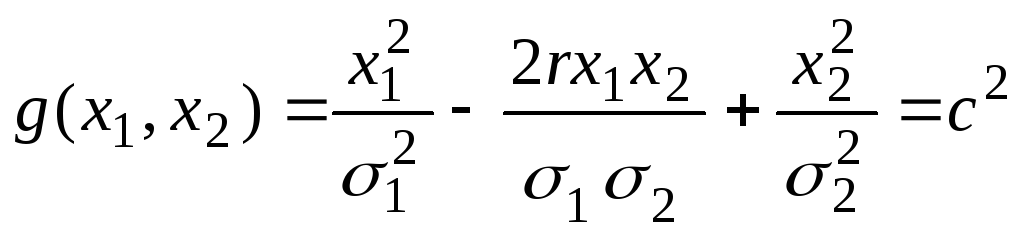

то, переходя к полярным координатам, можно показать, что [44, с. 68]

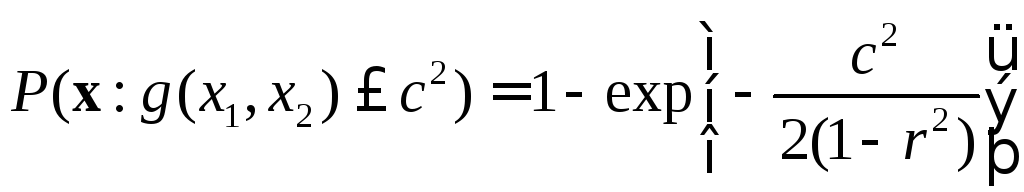. (3.38)

Для случая независимых случайных величин при эллипс превращается в окружность радиусоми, таким образом, из (3.38) получаем, что вероятность нахождения случайного вектора в круге с таким радиусом определяется введенным в разделе 2 распределением Рэлея

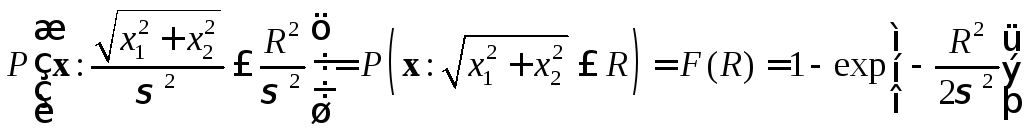, R>0. (1.39)

Круговая вероятная ошибка (КВО). Величина , соответствующая 50-процентному попаданию гауссовского случайного вектора в круг заданного радиуса, т.е. когда вероятность попадания равна 0,5, называетсякруговой вероятной ошибкой (КВО), а круг, соответственно, кругом равных вероятностей. В англоязычной литературе для круговой вероятной ошибки используется термин circular error probable (CEP).

Отметим, что для независимых случайных величин с равными СКО , 50-процентное попадание в круг (P=0,5) достигается при 1,177. Для круга радиуса обеспечивается попадание с вероятностьюP=0,997. В случае если радиус круга, при котором достигается вероятность попадания в него, равная 0,5, либо другой вероятности следует отыскивать с помощью соотношения (3.37).

Радиальная среднеквадратическая ошибка (Distance Root Mean Square (DRMS)

Эта ошибка определяется как

. (3.40)

Отметим, что вероятность попадания в круг такого радиуса составляет величину 0.65-0.68 в зависимости от значений параметров эллипса рассеивания.

Удвоенная радиальная среднеквадратическая ошибка (2DRMS).

Вероятность попадания в круг такого удвоенного радиуса зависит от конкретных соотношений СКО и коэффициента корреляции, а примерная ее величина определяется как P=0,95.

Понятия, аналогичные приведенным выше, используются и для трехмерного гауссовского вектора. При этом вводится величина сферической вероятной ошибки (СВО) и сферы равных вероятностей (spherical error probable (SEP) и sphere of equal probability (SEP)). Трехмерное гауссовское распределение широко используется при описании ошибок местоположения подвижных объектов в пространстве, в частности для летательных аппаратов.