4.4 Законы распределения функций случайных величин

В предыдущих разделах рассматривалась задача нахождения моментов для случайной величины и случайного вектора, полученных в результате преобразования некоторой исходной с.в. или случайного вектора с заданной плотностью распределения В настоящем подразделе обсуждается более сложная задача определения самой плотности распределения. для случайных величин и векторов, формируемых в результате их линейных и нелинейных преобразований.

Итак, предположим, что случайная величина получена в результате преобразования случайной величиныс известнойплотностью распределения .

Требуется найти плотность распределения , характеризующую свойства другойcлучайной величины . Для решения этой задачи сначала будем полагать, что -монотонная функция и таким образом существует взаимно однозначное соответствие между и во всей области их возможных значений. Это означает, что существует обратная функция такая, что. В этом случае очевидна справедливость следующих равенств:

-для возрастающей функции, т.е. при ;

-для убывающей функции, т.е. при .

Рис. 1.3.1. К определению вероятности

для возрастающей и убывающей функций

Отсюда, в частности, вытекает, что при

, (4.48)

т.е. вероятность для попасть в область совпадает с вероятностью для попасть в область (см. рис. 4.2).

Рис. 4.2. Области и ,

вероятности попадания в которые для с.в. исовпадают.

Поскольку итодля обеспечения (4.48) необходимо, чтобы в пределе.

Для убывающей функции знак у производной надо изменить на противоположный, так что в общем случае получаем

. (4.49)

Другое доказательство (Теория вероятностей и ее инженерные приложения).

Пусть.-непрерывная случайная величина с плотностью. Требуется найти закон распределения для случайной величины.

Пусть монотонна, непрерывна и дифференцируема в интервале

Тогда функция распределения случайной величины определяется по формуле

Если функция возрастает, то событиеэквивалентно событию, гдеесть функция обратная функции. Из строгой монотонностиследует однозначность функции Тогда

.

Дифференцируя это выражение по, входящей в верхний предел интеграла получим выражение для плотности

.

Если монотонно убывает, то событиеэквивалентно событию. Следовательно

.

Дифференцируя, получим

.

Так как плотность не может быть отрицательной, объединяя, получим

.

Если функция многозначна, то, разбивая область значений на участки, для которых она однозначна, и проводя аналогичные рассуждения, можно показать, что в этой ситуации справедливо следующее соотношение:

, (4.50)

где -функция на участках однозначности .

Пример

,

где -неслучайные величины. Найти плотность распределения для.

Решение. Найдем обратную функцию

.

Найдем призводную обратной функции

.

Найдем плотность

.

Пример.

,

Решение. Найдем обратную функцию

. Условиепереходит в условие ,

Найдем призводную обратной функции

.

Найдем плотность

.

Пример.

, .

Решение. Выше показано, что

.

Как следствие, имеем

а это нормальная плотность с параметрами ,.

Вывод. В результате линейного преобразования нормально распределенной величины получаем случайную величину распределенную по нормальному закону.

Пример. Пусть задана плотность распределения для случайной величины . Необходимо найтиплотность распределения квадрата от этой величины, т.е

. . (4.51)

Здесь каждому значению , которое всегда положительно, соответствуют два значения

и . (4.52)

Понятно, что если , тоэтому событию соответствуют два взаимно несовместных события или. Отсюда следует, что

или ,

т.е.

.

Принимая во внимание (4.50), для запишем

.

Таким образом, для искомой плотности распределения получаем

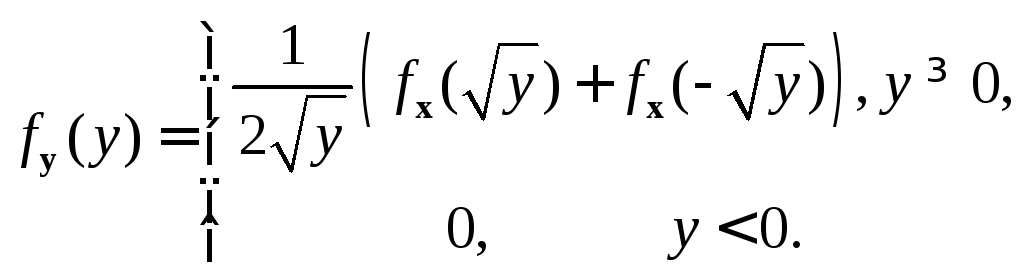(4.53)

Предположим, например, что случайная величина х является гауссовской, т.е. . В этом случае

, .

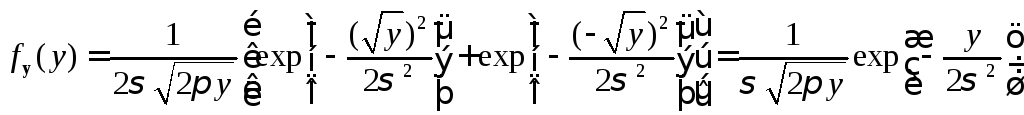Отсюда следует, что функция плотности для квадрата гауссовской случайной величины имеет вид

, . (4.54)

Графики этой функции плотности при разных значениях приведены на рис. 4.3.

Рис. 4.3. График плотности для при гауссовском характере плотности. для х .

Пример. Закон распределения модуля случайной величины

. (4.55)

Решение. Функция не монотонна.

.

Интервалы монотонности .

Как следствие, имеем

. (4.56)