Раздел 2. Случайные величины

2.1 Аксиоматическое определение вероятности

Современная теория опирается на определение вероятности с помощью трех основных аксиом

Сформулируем аксиоматическое определение вероятности.

Пусть -действительная скалярная функция, определенная на множестве событий.

Говорят, что является вероятностью событиятогда и только тогда, когда она удовлетворяет следующим трем аксиомам

1. для всех;

2. , где-выборочное пространство;

3. Для любой последовательности из попарно непересекающихся событий, т.е., где– пустое множество, справедливо равенство .

Для целей предлагаемого материала будем считать, что выборочным пространством является множество точек -мерного пространства. Далее пояснения проведем для простейшего случая, когда в качестве выборочного пространства выступает множествовсех действительных чисел на числовой оси. Будем называть ихэлементарными событиями.

На множестве введем класс подмножеств, включающий все открытые, закрытыеи полуоткрытые,интервалы, где-заданные действительные числа, принимающие произвольные известные значения, в том числе и . Кроме того, будем считать, что классу подмножествпринадлежат отдельные точки, все счетные объединения и пересечения интервалов и точек. Этот класс подмножествбудем называть возможнымисобытиями. Важно подчеркнуть, что при выполнении над элементами этого класса операций объединения, пересечения и дополнения вновь получается элемент, принадлежащий этому подмножеству, т.е. при выполнении перечисленных операций над событиями вновь получается событие.

2.2 Определение случайной величины и ее описание

Случайной называется такая величина, значение которой заранее неизвестно, и можно лишь указать некую числовую меру (вероятность) того, что она будет принадлежать той или иной заранее определенной области значений.

Три типа случайных величин:

-дискретные случайные величины у которых множество возможных значений конечно или счетно;

-непрерывные случайные величины у которых множество возможных значений несчетно;

-смешанные случайные величины у которых множество возможных значений несчетно;

Примеры:

1. Опыт- бросание игральной кости. Случайная величина-число выпавших очков. Множество возможных значений: --дискретная случайная величина.

2. Опыт-наработка прибора на отказ. Случайная величина-время наработки до первого отказа. Множество возможных значений--непрерывная случайная величина.

3. Опыт-проведение измерений значений некоторого параметра. Случайная величина -ошибка измерений. Множество возможных значений--непрерывная случайная величина.

4. Опыт-проведение измерений цифровым прибором с округлением результата. Случайная величина -ошибка округления. Множество возможных значений--непрерывная случайная величина.

Случайную величину будем считать заданной, если определена функция, позволяющая вычислять вероятность появления любого возможного события, т.е. вычислять вероятность того, что случайная величина примет какое-либо заданное значение, будет принадлежать тому или иному интервалу или их набору и т.д.

В качестве такой функции, в полном объеме определяющей свойства случайной величины, используется функция распределения вероятностей, или интегральная функция распределения, представляющая собой скалярную функцию действительного аргумента и определяющая вероятность того, что случайная величинапринадлежит открытому интервалу, т.е.вероятность того, что . Таким образом,

. (2.1)

Отметим, что при введении понятия случайной величины в качестве выборочного пространства не обязательно должно выступать все множество действительных чисел. Это может быть некоторая область на числовой оси, конечный или счетный набор чисел.

Свойства функции распределения вероятностей.

Функция распределения вероятностей является неотрицательной неубывающей, непрерывной слева функцией, удовлетворяющей условиям:

; (2.2)

. (2.3)

Эти свойства вытекают из определения функции распределения.

Функция распределения может иметь скачки (разрывы первого рода) и участки или постоянства или монотонного возрастания.

Зная функцию распределения случайной величины можно вычислить вероятности любых событий с нею связанных.

Вычисление вероятности попадания в интервал.

Как прямо следует из определения

.

Вычисление вероятности отдельного значения случайной величины.

.равнавеличине скачка функции распределения случайной величиныв точке.

Плотность распределения вероятности. Помимо функции распределения вероятности для описания свойств непрерывных случайных величин используют также плотность распределения вероятности, определяемую как

. (2.4)

Осуществляя интегрирование обеих частей (1.1.4) в пределах от дос учетом (1.1.2), устанавливается следующая связь между плотностью распределения вероятности и функцией распределения вероятностей

. (2.5)

Свойства плотности распределения вероятности.

Так как функция распределения вероятностей с ростом монотонно возрастает, топлотность распределения вероятности является всегда неотрицательной () обладающей свойством

. (2.6)

Используя полученные выше свойства можно показать, что для случайной величины, удовлетворяющей неравенству , справедливы следующие равенства:

, (2.7)

т.е. вероятность того, что случайная величинаокажется в границах отдоравнаприращению функции распределения на этом участке.

при этом . (2.8)

Принимая во внимание (1.1.4), можно также записать

;

и, как следствие, при малых имеем соотношение

. (2.9)

Пример равномерно распределенной на интервале случайной величины.

Функция распределения (2.10)

Плотность распределения (2.11)

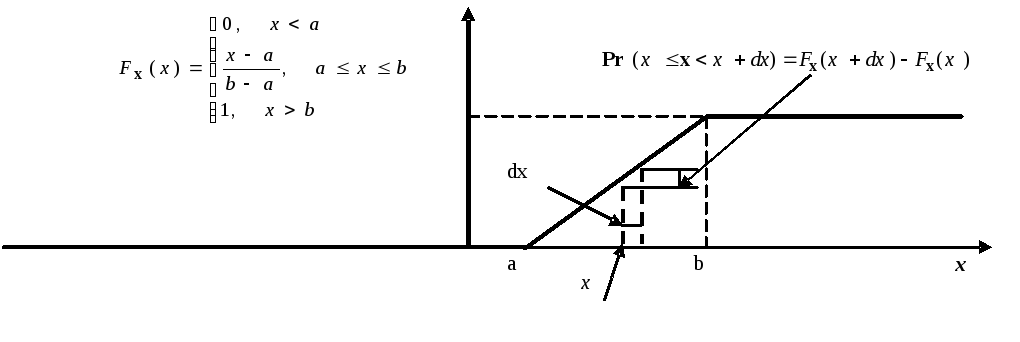
Рис. 2.1 Графики функции распределения. и функции плотности распределения. для случайной величины, равномерно распределенной

в интервале

Отметим, что в качестве здесь выступает множество всех чисел на интервале.

Для равномерно распределенной на интервале случайной величины, используя (2.10), (2.11),можем записать

. (2.12)

Очевидно, что вероятность попасть в любой принадлежащий подынтервал ширинойодинакова при любом его расположении внутри. Это, собственно, и обосновывает термин, используемый для случайной величины с таким распределением.