4.8. Линейные преобразования случайных векторов

Обсудим более подробно линейные преобразования случайных векторов. С этой целью рассмотрим достаточно простую, но весьма важную с практической точки зрения задачу.

Пусть задан -мерный вектор, который получен в результате линейного преобразования-мерного вектора, т.е.

, (4.94)

и требуется найти его математическое ожидание и матрицу ковариаций.

Решение этой задачи легко получить, если воспользоваться соотношениями (1.2.9), (1.2.10). В первое подставляется , а во второе. В этом случае можем записать:

;

Таким образом, получаем

, (4.95)

. (4.96)

Отсюда следует, что для нахождения математического ожидания и матрицы ковариаций вектора , формируемого в результате линейного преобразования (4.94), не требуется знания функции плотности для исходного вектора, а достаточно располагать для него лишь значениями математического ожидания и матрицы ковариаций.

t Пример 1. Пусть задан вектор , включающий два подвектораиразмерностии, т.е.

, (4.97)

и для него определены математическое ожидание и матрица ковариаций в виде:

; (4.98)

, (4.99)

где -матрица, характеризующая взаимную корреляцию двух векторов.

Требуется найти математическое ожидание и матрицу ковариаций вектора

. (4.100)

Принимая во внимание (1.3.22), (1.3.23), легко получить

, (4.101)

. (4.102)

Из рассмотренного примера, в частности, следует, что для вектора

, (4.103)

его математическое ожидание и матрица ковариаций определяются как:

; (4.104)

. (4.105)

Очевидно, что если векторы инекоррелированы, то

. (4.106)

Если предположить, что в соотношении (1.3.21) вектор гауссовский, т.е.

, (4.107)

то, как отмечалось, вектор также будет гауссовским, а его плотность будет иметь вид

. (4.108)

П р и м е р . Пусть размерности иодинаковы, а матрицав (4.94) не вырождена. Убедимся, что если- гауссовский, то также будет гауссовским.

Принимая во внимание равенства [8] и используя (1.2.11), можно записать:

;

; .

Таким образом, легко убедиться в справедливости (1.3.35), поскольку

.

Если предположить, что совместное распределение двух векторов игауссовское

, (4.109)

то вектор , определяемый согласно(1.3.27), также будет гауссовским, т.е.

, (4.110)

а параметры этой плотности. будут задаваться соотношениями (1.3.28), (1.3.29).

4.9. Определение статистических свойств длины проекции случайного двухмерного вектора на заданное направление

Задача определения статистических свойств длины проекции случайного вектора на заданное направление достаточно часто возникает при обработке навигационной информации. Например, при движении судна вдоль фарватера наиболее важной представляется величина ошибки определения координат места в направлении поперек фарватера. Полагая, что ошибка определения координат судна на плоскости описывается как двухмерный случайный вектор, величина ошибки вдоль фарватера может быть найдена в результате решения задачи, которая формулируется следующим образом.

Задан двухмерный случайный вектор с математическим ожиданиеми матрицей ковариаций

. (4.111)

Требуется найти математическое ожидание и дисперсию скалярной случайной величины , связанной скак

, (4.112)

где ,- известные числа.

Задача такого типа уже рассматривалась. Заметим, что ее решение также может быть легко получено с использованием (4.95), (4.96), если в качестве принять. В результате имеем

, (4.113)

. (4.114)

Конкретизируем эту задачу, полагая, что компоненты - координаты точки на плоскости, и требуется найти статистические характеристики случайной величины , определяющей длину проекции векторана некоторое произвольное направление, задаваемое единичным вектором (рис. 4.4)

. (4.115)

Рис. 4.4. Определение проекции вектора на единичное направление

Поскольку величина, определяющая с учетом знака длину проекции, может быть представлена в виде

, (4.116)

для ее математического ожидания и дисперсии можно записать:

; (4.117)

. (4.118)

В частности, если - центрированный вектор, то величина, определяющая с учетом знака длину проекции на произвольное направление, также будет представлять собой центрированную случайную величину с дисперсией, задаваемой соотношением (1.3.45).

Обращаем внимание на то, что дисперсия (1.3.45) может быть представлена в виде квадратичной формы

.

При изменении направления единичного вектора(1.3.42) очевидно, что меняется и значение дисперсии.

Интересной представляется задача нахождения таких значений углов, при которых дисперсия принимает минимальное и максимальное значения. Фактически это есть известная задача нахождения минимального и максимального значений квадратичной формы на единичной окружности [8]. Ее решение определяют собственные числа матрицы ковариаций (1.3.38), характеризующие максимальное и минимальное,значения дисперсии, и соответствующие им собственные векторы. Если изначально матрица ковариаций диагональная, то направления, соответствующие наибольшему и наименьшему значениям дисперсий, совпадают с направлениями координатных осей, при этом,.

Из сказанного выше также следует, что если вектор , задающий ошибку местоположения на плоскости, гауссовский, то величина, определяющая с учетом знака длину его проекции на заданное направление, также будет иметь гауссовскую плотность. с математическим ожиданием (4.117) и дисперсией (4.118). Знание прлотности для этой величины позволяет в полном объеме описать свойства ошибки вдоль заданного направления, что весьма важно при решении ряда задач обработки навигационной информации.

Пример. Пусть компоненты двухмерного центрированного гауссовского вектора описывают ошибки местоположения на плоскости относительно некоторой заданной точки, и матрица ковариаций этого вектора имеет вид:. Требуется найти плотность и ее параметры для случайной величины, определяющей длину проекции в направлении прямой, расположенной под углом 30° относительно оси (рис. 4.5).

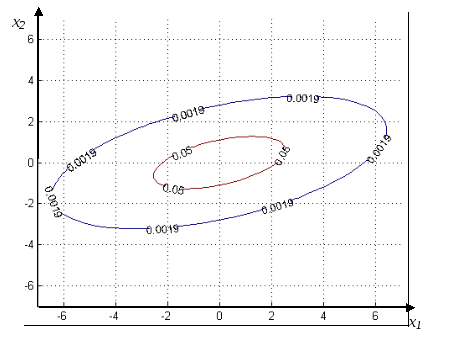
Рис. 4.5. График плотности распределения двухмерного гауссовского вектора

и соответствующего ей эллипса

Рис. 4.6. График ф.п.р.в. для при =30°,

Используя (4.118), при =30°, ,,найдем значение дисперсии, которое будет равно 2,62. С учетом вышесказанного можем сделать вывод о том, что ошибка в направлении=30° представляет собой гауссовскую плотность распределения (4.6).