2.3 Статистические ( числовые) характеристики случайных величин

Для описания статистических свойств случайных величин используется также набор ее числовых (не случайных) характеристик. Основными из них являются: математическое ожидание, моменты, дисперсия, среднеквадратическое отклонение (СКО); для СКО иногда используют термин стандартное отклонение или стандарт. Если речь идет об ошибке, то используется термин среднеквадратическая ошибка. В англоязычной литературе для среднеквадратической ошибки используют термин Root Mean Square Error (RMSE).

Математическое ожидание дискретной случайной величины.

Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных ее значений на вероятности этих значений

(2.14)

фактически представляющее собой средневзвешенное значение случайной величины.

Математическое ожидание непрерывной случайной величины.

Математическое ожидание непрерывной случайной величиныопределяется выражением

. (2.15)

Математическое ожидание смешанной случайной величины.

Математическое ожидание смешанной случайной величины определяется выражением

, (2.16)

где -множество участков непрерывности функции.

Случайная величина, имеющая нулевое математическое ожидание, называется центрированной случайной величиной.

Моменты. Дисперсия. Среднеквадратическое отклонение.

Начальным моментом порядкаслучайной величины называется математическое ожидание степениэтой величины:

-для дискретной случайной величины

, (2.17)

-для непрерывной случайной величины

, (2.18)

-для смешанной случайной величины

. (2.19)

Наряду с начальными моментами используются центральные моменты.

Центральным моментом порядкаслучайной величины называется математическое ожидание степени величины :

-для дискретной случайной величины

, (2.20)

-для непрерывной случайной величины

, (2.21)

-для смешанной случайной величины

. (2.22)

Особое значение для практики имеет второй центральный момент или дисперсия случайной величины .

Дисперсия есть характеристика рассеивания относительно математического ожидания.

-для дискретной величины; (2.23)

-для непрерывной величины. (2.24)

Иногда используют среднее квадратическое отклонение (СКО), определяемое как

. (2.25)

Для непрерывной случайной величины, когда известна ее плотность распределения, выражения для расчета числовых характеристик сведены в таблицу

Т а б л и ц а 2.1

Основные числовые характеристики случайной величины

Характеристика	Определение
Математическое ожидание	(2.27)
Момент n-го порядка	(2.28)
Центральный момент n-го порядка	(2.29)
Дисперсия	(2.30)
Среднеквадратическое отклонение (СКО)	(2.31)

П р и м е ч а н и е. В приведенных соотношениях пределы интегрирования считаются бесконечными. В дальнейшем, когда пределы не указываются, они предполагаются бесконечными.

Пример. Числовые характеристики для равномерно распределенной случайной величины.

;

;

.

Частные случаи.

1. При :,,,.

2. Для симметричной плотности распределения (в пределах ), математическое ожидание, как и следует ожидать, будет нулевым,

,

при этом второй момент и дисперсия совпадут между собой

.

Связь между вторыми начальными и центральными моментами.

Отметим, что, учитывая (1.1.14), (1.1.16), можно получить также следующее выражение для дисперсии

. (2.32)

Свойства числовых характеристик.

Из определения математического ожидания и дисперсии вытекает ряд простейших и очевидных свойств этих характеристик:

-математическое ожидание неслучайной величины равно самой этой величине

.

-дисперсия неслучайной величины равнанулю

.

-математическое ожидание суммы случайной величины инеслучайной величины определяется выражением

-дисперсия суммы случайной величиныинеслучайной величины равна дисперсии случайной величины

.

- математическое ожидание произведения случайной величинынанеслучайной величину равно произведениюматематического ожидания случайной величины на неслучайную величину

.

-дисперсия произведения случайной величинынанеслучайную величину определяется выражением

.

Важное свойство дисперсии.

Дисперсия случайной величины характеризует степень ее концентрации в окрестности математического ожидания. Этот факт находит свое отражение в неравенстве П.Л.Чебышева суть которого заключается в следующем:

Для случайной величины с математическим ожиданиеми дисперсией, при любом, можно записать следующее выражение:

. (2.33)

Действительно,

(2.34)

откуда и следует (2.33).

Неравенство П.Л.Чебышева фактически означает, что при уменьшении дисперсии уменьшается вероятность того, что случайная величина выйдет за пределы отрезка .

Другие числовые характеристики.

При решении прикладных задач обработки информации важной характеристикой случайной величины является квантиль.

Квантилем порядка с.в.называется такая величина, для которой выполняется соотношение

, (2.35)

т.е. -величина, при которой обеспечивается заданный уровень вероятности (рис. 1.1.2).

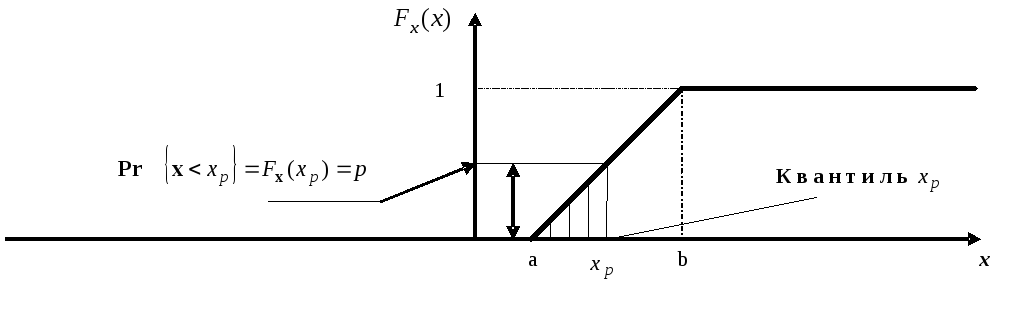
Рис. 2.2. К определению квантили

Квантиль 50-процентного уровня вероятности (квантиль порядка ) называетсямедианой распределения. Иными словами, медиана-это величина, при которой , а следовательно,

,

т.е. площади слева и справа от значения медианы для фигур, образованных плотностью распределения. и осью абсцисс, равны между собой.

Введем еще одну числовую характеристику, называемую модой. Модой случайной величины называется такое значение при котором плотность распределения имеет локальный максимум. В случае, когда плотность распределения имеет один максимум, она называетсяунимодальной.

Отметим, что для равномерно распределенной случайной величины плотность. не имеет максимумов, а медиана совпадает с математическим ожиданием.

Пример плотности распределения имеющей две моды.

представляющее собой среднее арифметическое двух гауссовских плотностей

Рис. 2.3. Пример плотности распределения., имеющей две моды

Расчет характеристик случайной величины после ее преобразования.

Предположим, что с помощью некоторой в общем случае нелинейной функции в результате преобразования случайной величиныс известной плотностью.сформирована новая случайная величина... Здесь справедливы следующие соотношения :

, (2.36)

. (2.37)

Из этих соотношений следует, что для нахождения моментов преобразованной случайной величины необходимо знать плотность для исходной случайной величины и вычислить соответствующие интегралы. Задача упрощается, если функция, с помощью которой осуществляется преобразование, является линейной. В этом случае достаточно знать только соответствующие моменты для исходной cлучайной величины.

Пример. Пусть , гдеи- известные детерминированные величины, а – случайная величина. с математическим ожиданиеми дисперсией. Найдем математическое ожидание и дисперсию для. Используя приведенные выражения, нетрудно записать:

;

.