Раздел 4. Преобразование случайных величин.

1. Преобразование случайных величин. Основные задачи преобразования.

Предположим, что с помощью некоторой в общем случае нелинейной функции в результате преобразования случайной величиныс известной плотностью.сформирована новая случайная величина

. (4.1)

Три задачи:

- зная закон распределения совокупности случайных величин определить закон распределения функции случайных величин;

- зная закон распределения совокупности случайных величин определить числовые характеристики функции случайных величин;

- зная числовые характеристики совокупности случайных величин определить числовые характеристики функции случайных величин;

В этом случае для расчета вероятности можно воспользоваться неравенством Чебышова, суть которого заключается в следующем:

Для случайной величины с математическим ожиданиеми дисперсией, при любом, можно записать следующее выражение:

. (4.2)

1. Расчет числовых характеристик для случайной функции одного случайного аргумента.

Пусть .

Дискретное распределение

Математическое ожидание:

. (4.3)

Дисперсия:

. (4.4)

Аналогично определяются начальные и центральные моменты высших порядков.

Непрерывное распределение

, (4.5)

. (4.6)

Аналогично определяются начальные и центральные моменты высших порядков.

Из этих соотношений следует, что для нахождения моментов преобразованной случайной величины необходимо знать плотность для исходной случайной величины. и вычислить соответствующие интегралы. Задача упрощается, если функция, с помощью которой осуществляется преобразование, является линейной. В этом случае достаточно знать только соответствующие моменты для исходной cлучайной величины.

Пример. Пусть , гдеи- известные детерминированные величины, а – случайная величина. с математическим ожиданиеми дисперсией. Найдем математическое ожидание и дисперсию для. Используя приведенные выражения, нетрудно записать:

;

4.3 Числовые характеристики от функций случайных величин.

Как и в скалярном случае, располагая случайным вектором с известной совместной плотностью распределения., можно с помощью некоторой в общем случае нелинейной функциисформировать новый случайный вектор.. Математическое ожидание и матрица ковариаций для нового векторамогут быть найдены с помощью следующих соотношений:

; (4.7)

. (4.8)

Пусть

. (4.9)

Математическое ожидание суммы случайных величин

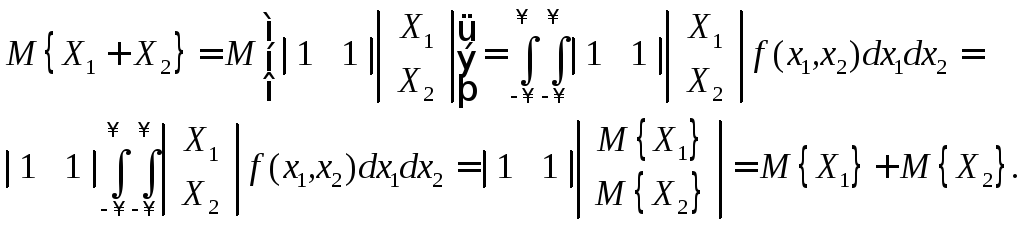(4.10)

Другое доказательство выражения

.

Действительно,

т.е. математическое ожидание суммы случайных величин равно сумме математических ожиданий случайных величин.

Дисперсия линейной комбинации случайных величин

(4.11)

Частный случай: дисперсия суммы случайных величин

, где ,.

.

т.е дисперсия суммы случайных величин равна сумме всех элементов ковариационной матрицы.

Если и-некоррелированы ( и, как следствие ,) имеем

Пример.. Пусть для двух случайных величин изаданы математические ожидания,, дисперсии,и коэффициент корреляции. Требуется найти математическое ожидание и дисперсию случайной величины, формируемой как, гдеи- известные коэффициенты.

С использованием (4.9), (4.11) можем записать:

;

.

Математическое ожидание произведения случайных величин

, где -скаляры

, где -векторы.

Если случайные величины не коррелированны, то

,

.

Математическое ожидание и дисперсия среднего арифметического независимых наблюдений

, (4.12)

где - случайная величина с математическим ожиданиеми дисперсией

Имеем

.

, (4.13)

Как следствие, . (4.14)

Числовые характеристики минимальной из двух величин: случайной и не случайной

Имеется непрерывная случайная величина с плотностью.

Найти параметры для функции

. (4.15)

Можем записать

. (4.16)

Тогда

, (4.17)

где -функция распределения случайной величины.

Найдем второй начальный момент

.

Откуда

. (4.18)

Числовые характеристики максимальной из двух величин: случайной и неслучайной

. (4.19)

Можем записать

. (4.20)

, (4.21)

; (4.22)

. (4.23)

Числовые характеристики функции

(4.24)

Решение.

, (4.25)

, (4.26)

. (4.27)

Числовые характеристики минимальной из двух случайных величин

, (4.28)

где-независимые случайные величины с плотностямии.

Решение. Рассмотрим гипотезу, что случайная величина попала в в элементарный интервал.Вероятность этой гипотезы есть элемент вероятности.

Условное математическое ожидание величины при этой гипотезе будет равно

. (4.29)

Тогда по интегральной формуле математического ожидания получим

(4.30)

Найдем второй начальный момент

. (4.31)

Тогда .

Еслираспределены одинаково, т.е. с плотностью,

имеем

Числовые характеристики максимальной из двух случайных величин

, (4.32)

где-независимые случайные величины с плотностямии.

Решение.

(4.33)

(4.34)

Еслираспределены одинаково, т.е.с плотностью,

имеем

Числовые характеристики модулей функций случайных величин

1. Числовая величина , (4.35)

где - непрерывная случайная величина с плотностью,-неслучайная величина.

Решение. Функцияможет быть определена как

Как следствие,

(4.36)

, (4.37)

.

2. , (4.38)

где-независимые случайные величины с плотностямии.

Решение. Рассмотрим гипотезу. Вероятность этой гипотезы-элемент вероятности.

Условное математическое ожидание с учетом соотношений, полученных выше, будет равно

.

По формуле полного математического ожидания получим

(4.39)

Из симметрии относительно величин иследует, что

Тогда

. (4.40)

Второй начальный момент можно найти непосредственно

Так как

Имеем

(4.41)

.

Числовые характеристики функций нормально распределенных случайных величин.

1. . (4.42)

Решение. Обозначим и найдем характеристики для.

.

.

Но случайная величина распределена по нормальному закону и, следовательно,

.

Откуда

.

Как следствие,

, (4.43)

. (4.44)

Частный случай: если , то распределение случайной величиныназывается( « хи квадрат» )-распределением, при этом

; .

2. . (4.45)

Тогда

, (4.46)

. (4.47)