Исходя из перечисленных выше требований, для многофакторной корреляционной модели уровня среднесуточной производительности локомотива в грузовом движении (Y) возьмём следующие факторы:

X₁ – средний вес поезда, тонны;

X₂ – среднесуточный пробег локомотива в грузовом движении, км;

X₃ – средняя статическая нагрузка на вагон, тонны;

X₄ – грузооборот, млн. тариф. т-км;

X₅ – средняя участковая скорость движения грузовых поездов, км/ч;

X₆ – полное время оборота вагона, сутки.

Исходная информация представлена в табл. 6.6.

Таблица 6.6

Исходные данные для корреляционного анализа

Рассчитаем матрицу парных коэффициентов корреляции (табл. 6.7).

Таблица 6.7

Матрица парных коэффициентов корреляции

Коэффициенты парной корреляции характеризуют тесноту связи между двумя показателями в общем виде с учётом взаимосвязей факторов, оказывающих воздействие на результативный показатель.

Данные табл. 6.7 (первый столбец) свидетельствуют об ощутимом воздействии на уровень среднесуточной производительности локомотива таких факторов, как средний вес поезда, среднесуточный пробег локомотива в грузовом движении и средняя статическая нагрузка на вагон. Так как коэффициенты парной корреляции у данных показателей имеют существенную величину, то их можно выбрать для построения многофакторной корреляционной модели.

Чаще всего на практике применяется линейное уравнение множественной регрессии

y = a₀ + a₁x₁ + a₂x₂ +…+ a_nx_n, (6.8)

где y – результативный показатель; x₁, x₂,… x_n – факторы; a_i – параметры уравнения.

Для определения коэффициентов регрессионного уравнения (6.8) удобнее всего использовать методы матричного исчисления. Для этого сделаем одно допущение, которое не меняет условия задачи. Будем считать, что в уравнении (6.8) свободный член a₀ всегда умножается на некоторый фиктивный фактор, имеющий постоянное значение, равное единице, т.е. имеем

y = a₀x₀ + a₁x₁ + a₂x₂ +…+ a_nx_n.

В исходной статистической матрице (6.9), составленной по данным табл. 6.6, появляется ещё один столбец, все значения которого равны единице.

. (6.9)

Введём также вектор результативного показателя (6.10):

. (6.10)

Для расчёта параметров уравнения регрессии воспользуемся формулой (6.11):

(6.11)

В нашем примере параметры уравнения регрессии равны:

a₀ = -351,057; a₁ = 0,512; a₂ = 1,787; a₃ = -17,658. Таким образом, уравнение зависимости производительности локомотива от среднего веса поезда, среднесуточного пробега локомотива и статической нагрузки на вагон будет иметь следующий вид:

y = -351,057 + 0,512x₁ + 1,787x₂ – 17,658x₃. (6.12)

На следующем этапе анализа необходимо убедиться в значимости полученной модели. Выдвигаем нулевую гипотезу Н₀: а₁=а₂=…=а_m=0 (регрессии нет). Конкурирующая гипотеза – хотя бы один коэффициент регрессии отличен от нуля.

Методика проверки разработана Фишером. В её основе лежит дисперсионный анализ. В качестве меры факторного влияния используется величина

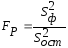, (6.13)

где 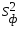- факторная дисперсия, характеризующая изменчивость результативного показателя под действием факторов;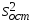- остаточная дисперсия, применяемая здесь в качестве оценки дисперсии случайной составляющей.

Факторная дисперсия определяется по формуле 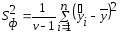(6.14):

. (6.14)

Остаточная дисперсия определяется по формуле (6.15):

, (6.15)

где v – число оцениваемых параметров, учитывая свободный член уравнения; 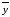- среднее арифметическое значение результативного показателя;- расчётное значениеy, соответствующее i-му наблюдению, n – количество наблюдений.

В нашем примере ;.

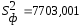Таким образом, .

Фактическая величина F-отношения сопоставляется с табличной и делается заключение о надёжности связи. F-теоретическое рассчитывается по таблице значений F с k₁ = (v – 1) и k₂ = (n – v) степенями свободы. При уровне вероятности p = 0,05 и количестве степеней свободы k₁=3 и k₂=5 F-теоретическое составляет 5,41. Поскольку F_Р>F_ТАБ, то гипотеза об отсутствии регрессии отклоняется. Это свидетельствует о значительной тесноте связи между изучаемыми показателями.

Для статистической оценки точности уравнения регрессии рассчитывается также средняя ошибка аппроксимации:

. (6.16)

Чем меньше теоретическая линия регрессии (рассчитанная по уравнению) отклоняется от фактической, тем меньше средняя ошибка аппроксимации. В нашем примере она составляет 1,038 %. Учитывая, что в экономических расчётах допускается погрешность 5-8 %, можно сделать вывод, что исследуемое уравнение регрессии довольно точно описывает изучаемые зависимости. А значит, его можно использовать для практических целей.

Вопросы для обсуждения

1. Перечислите условия применения корреляционного метода.

2. Что показывает уравнение регрессии?

3. В какой последовательности применяется корреляционно-регрессионный метод изучения линейной и нелинейной форм связи?

4. Каковы условия отбора факторов для корреляционного анализа?

5. На основе расчёта каких показателей даётся статистическая оценка результатов корреляционного анализа?

7. Системный подход к экономическому анализу

и поиск резервов повышения эффективности производства

(перевозок, работ, услуг)

7.1. Сущность системного подхода

к изучению хозяйственной деятельности филиалов ОАО «РЖД»

Системный анализ – это совокупность научных методов и приёмов решения разнообразных проблем, возникающих в процессе деятельности общества.

Выделяют несколько этапов проведения системного анализа.

На первом этапе объект исследования представляется как система, для которой определяют цели и условия функционирования. Хозяйственную деятельность предприятия можно рассматривать как систему, состоящую из трёх взаимосвязанных элементов: ресурсов, производственного процесса и готовой продукции. Входом этой системы являются материально-вещественные потоки ресурсов (средств и предметов труда) и потоки трудовых ресурсов. Выходом – материально-вещественные потоки готовой продукции (перевозки, работы, услуги). Производственный процесс переводит вход системы в её выход, т.е. в результате производственного процесса производственные ресурсы, соединяясь, становятся готовой продукцией. Целью работы любого предприятия, в том числе и транспортного, является рентабельность, т.е. по возможности высокий результат в денежном выражении за рассматриваемый период времени. Задача системного анализа – рассмотреть все частные факторы, обеспечивающие более высокий уровень рентабельности. Экономический принцип деятельности предприятия – обеспечение либо максимального выпуска продукции (работ, услуг) при данных затратах ресурсов, либо альтернативно заданного выпуска продукции (работ, услуг) при минимальном расходе ресурсов. Условия функционирования транспортного предприятия определяются системой долговременных экономических нормативов налогообложения и внешнеэкономическими связями предприятия, т.е. рынком финансирования, рынком купли и рынком продажи.

Для проведения системного экономического анализа необходима разработка качественных характеристик экономики предприятия – системы синтетических и аналитических показателей. Отбор показателей, характеризующих финансово-хозяйственную деятельность предприятия, осуществляется на втором этапе анализа.

На третьем этапе проведения системного экономического анализа составляется общая схема системы, устанавливаются её главные компоненты, функции, взаимосвязи, разрабатывается схема подсистем, показывающая соподчинение их элементов.

На основе информационной модели хозяйственной деятельности, т.е. модели формирования экономических факторов и показателей, составляется

общая блок–схема комплексного экономического анализа, классифицируются факторы и показатели, формализуются связи между ними (рис. 7.1).

Рис. 7.1. Общая блок – схема взаимосвязи показателей

деятельности предприятия для комплексного анализа

Связь между различными сторонами производственно-хозяйственной деятельности отражается на схеме в определённой соподчинённости различных показателей.

В основе всех экономических показателей лежит предварительный обзор обобщающих показателей, который предполагает характеристику наличия необходимых материальных и финансовых ресурсов для нормального функционирования транспортного предприятия и выполнения его производственной программы. Затем проводится анализ организационно-технического уровня, т.е. производственной структуры предприятия, структуры управления, уровня концентрации и специализации производства, продолжительности производственного цикла, технической и энергетической вооружённости труда, степени механизации и автоматизации. Параллельно с организационно-техническим уровнем даётся оценка маркетинговой деятельности предприятия по изучению спроса на продукцию транспорта, её конкурентоспособности, конъюнктуры рынка, рекламы и т.д.

Показатели блока 1 и блока 2 оказывают влияние на все остальные показатели хозяйствования и в первую очередь на объём производства транспортной продукции, её качество, на степень использования производственных ресурсов (производительность труда, фондоотдачу, материалоотдачу), а также на другие показатели экономической эффективности: себестоимость, прибыль, рентабельность и т.д.

Эффективность использования производственных ресурсов проявляется в трёх направлениях: