Таблица 5.4

Исходные данные для сравнительной комплексной оценки

деятельности железной дороги таксонометрическим методом

Пример расчёта значений показателей в табл. 5.4:

Значение показателя объёма перевозок в 2001 г. определяется по формуле (5.5) и составляет ; значение показателя объёма перевозок в 2002 г. составляети т.д.

Значение показателя объёма эксплуатационных расходов в 2001 г. составляет и т.д.

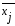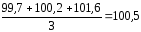При этом среднее значение () по показателю объёма перевозок рассчитывается по формуле (5.6) и составляет; среднее значение по показателю объёма эксплуатационных расходов составляет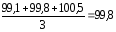и т.д.

Среднеквадратичное отклонение (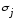) по показателю объёма перевозок определяется по формуле (5.7) и составляет: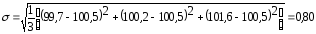и т.д.

Результаты сравнительной комплексной оценки таксонометрическим методом представлены в табл. 5.5.

Таблица 5.5

Результаты расчёта сравнительной комплексной оценки

таксонометрическим методом

Например, комплексная оценка за 2001 г. рассчитывается следующим образом:

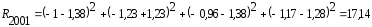и т.д.

Сводка результатов расчётов по трём методам приведена в табл. 5.6.

Таблица 5.6

Сводка результатов сравнительной комплексной оценки

Данные табл. 5.6 показывают, что по всем вариантам расчёта наилучшие результаты достигнуты железной дорогой в 2003 г., на втором месте находится 2002 г., на третьем – 2001 г., то есть в данном случае распределение лет, занявших первое и последнее места, одинаково независимо от метода расчёта и системы показателей. Это свидетельствует об «индивидуализированных» результатах деятельности железной дороги.

Вопросы для обсуждения

1. Чем объясняется необходимость сравнительной комплексной оценки деятельности предприятия?

2. Приведите алгоритмы многомерных сравнений для комплексной оценки хозяйственной деятельности.

3. Каковы условия применения коэффициентов сравнительной значимости в ходе комплексной оценки результатов хозяйственной деятельности?

6. Способы изучения корреляционных (стохастических) взаимосвязей

показателей работы железнодорожного транспорта

6.1. Понятие стохастической связи и задачи корреляционного анализа

Стохастические зависимости чаще встречаются в экономических исследованиях, чем функциональные. Они отличаются приблизительностью, неопределённостью, проявляются только в среднем и по значительному количеству наблюдений (объектов). При стохастической зависимости каждой величине факторного показателя (аргумента) может соответствовать несколько значений результативного показателя (функции). Отличают парную и множественную корреляцию.

Парная корреляция – это связь между двумя показателями, один из которых является факторным, а другой – результативным.

Множественная корреляция возникает от взаимодействия нескольких факторов с результативным показателем.

Наиболее широкое применение в экономических исследованиях нашли приёмы корреляционного анализа, которые позволяют количественно выразить взаимосвязь между показателями.

Условия применения корреляционного анализа

1. Наличие достаточно большого количества наблюдений о величине исследуемых факторных и результативных показателей (в динамике или за текущий год по совокупности однородных объектов).

2. Исследуемые факторы должны иметь количественное измерение и отражение в тех или иных источниках информации.

Применение корреляционного анализа позволяет решить следующие задачи:

Исследование корреляционных соотношений имеет огромное значение в экономическом анализе. Это проявляется в том, что значительно углубляется факторный анализ, устанавливается место и роль каждого фактора в формировании уровня исследуемых показателей, углубляются знания об изучаемых явлениях, определяются закономерности их развития и, как итог, – точнее обосновываются планы и управленческие решения, более объективно оцениваются итоги деятельности предприятий и более полно определяются внутрихозяйственные резервы.

6.2. Использование способов парной корреляции

для изучения стохастических зависимостей

Одной из основных задач корреляционного анализа является определение влияния факторов на величину результативного показателя (в абсолютном измерении). Для решения этой задачи подбирается соответствующий тип математического уравнения, которое наилучшим образом отражает характер изучаемой связи (прямолинейной, криволинейной и т.д.). Это играет важную роль в корреляционном анализе, потому что от правильного выбора уравнения регрессии зависит ход решения задачи и результаты расчётов.

Наиболее простым уравнением, которое характеризует прямолинейную зависимость между двумя показателями, является уравнение прямой

Y_X = а + bx, (6.1)

где x – факторный показатель; Y – результативный показатель; a и b – параметры уравнения регрессии, которые требуется определить.

Данное уравнение описывает такую связь между двумя признаками, при которой с изменением факторного показателя на определённую величину наблюдается равномерное возрастание или убывание значений результативного показателя. В качестве примера для иллюстрации корреляционного анализа прямолинейной зависимости могут быть использованы сведения об изменении среднесуточной производительности грузового вагона в зависимости от средней статической нагрузки на вагон (табл. 6.1).

Таблица 6.1

Исходные данные для определения тесноты связи

между среднесуточной производительностью грузового вагона

и средней статической нагрузкой

Определим среднеарифметические значения показателей Y и x по формулам (6.2) и (6.3):

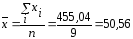; (6.2)

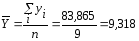, (6.3)

где n = 9, i = 1,….,9.

Дальнейшим вычислениям придаётся табличная форма, что повышает их наглядность (табл. 6.2).

Таблица 6.2

Расчёт производных величин для определения параметров уравнения связи

и коэффициента корреляции

Теснота связи между показателями производительности вагона и средней статической нагрузкой измеряется коэффициентом корреляции, который исчисляется по формуле 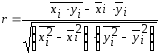(6.4).

. (6.4)

Подставляя необходимые значения в формулу (6.4), получаем

.

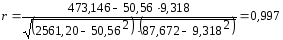Коэффициент корреляции может принимать значения от 0 до 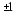. Чем ближе его величина к 1, тем более тесная связь между изучаемыми явлениями, и наоборот. В данном случае величина коэффициента корреляции является весьма высокой (табл. 6.3). Это позволяет сделать вывод о том, что средняя статическая нагрузка на вагон является основным фактором, от которого зависит среднесуточная производительность грузового вагона.

Таблица 6.3

Качественная оценка тесноты связи при различных значениях

коэффициента корреляции и корреляционного отношения

Если коэффициент корреляции возвести в квадрат, получим коэффициент детерминации (d = 0,994). Он показывает, что производительность грузового вагона на 99,4 % зависит от средней статической нагрузки на вагон, а на долю других факторов приходится 0,6 % прироста производительности.

Считая формулу связи линейной (y = a + bx), определим параметры a и b с помощью системы нормальных уравнений:

;

.

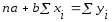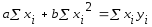Значение определяем из первого уравнения:

9a + 455,04b = 83,865;

455,04a + 23050,82b = 4258,32;

Подставляя найденное значение во второе уравнение, находим значениеb: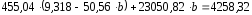

;

.

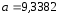Итак, уравнение регрессии в окончательном виде получило следующий вид:

.

В случае, если с помощью корреляционного анализа линейная связь между показателями не обнаружена, определяется возможность криволинейной зависимости: