Материал презентаций по физике / Лекции для заочников / Физика для гуманитариев_1 / Вотинов_Перминов_Физика

откуда видно, что средняя кинетическая энергия поступательного движения молекулы пропорциональна абсолютной температуре:

а для средней квадратичной скорости

Только поступательно движутся лишь одноатомные молекулы. Двух- и многоатомные молекулы, кроме поступательного, могут совершать также вращательное и колебательное движения. Эти виды движения связаны с некоторым запасом энергии, вычислить который позволяет закон о равномерном распределении кинетической энергии по степеням свободы молекулы. При любом числе степеней свободы (см. разд. 1.1) молекулы три — поступательные, причем ни одна из них не имеет преимущества перед другими. На три поступательные степени свободы приходится энергия, равная 3kT2, следовательно, на каждую поступательную степень свободы приходится в среднем одинаковая энергия, равная 1/2kT.

В соответствии с законом о равномерном распределении кинетиче- ской энергии по степеням свободы на каждую степень свободы молекулы приходится в среднем одинаковая кинетическая энергия, равная

1/2kT.

Если между атомами в молекуле действует квазиупругая сила, то следует учесть, что при колебательном движении среднее значение кинетической энергии равно среднему значению потенциальной, поэтому колебательная степень свободы обладает удвоенной энергетической емкостью.

Таким образом, для средней энергии молекулы получается выражение

ãäå i — сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы:

71

Следует отметить, что при температурах ниже 1000 К связи между атомами можно рассматривать как жесткие.

Для молекул с жесткой связью между атомами i совпадает с числом степеней свободы молекулы (поступательных и вращательных).

Закон Максвелла распределения молекул идеального газа по скоростям

В результате многократных соударений скорость каждой молекулы изменяется по модулю и направлению. Однако из-за хаотического движения молекул все направления движения являются равновероятными, т. е. в любом направлении в среднем движется одинаковое количество молекул. Согласно молекулярно-кинетической теории, как бы ни изменялись скорости молекул при столкновениях, средняя квадратичная скорость (2.20) молекул газа массой m в газе, находящемся в состоянии равновесия при T = const, остается постоянной. Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, подчиняющееся вполне определенному закону. Этот закон теоретически выведен Дж. Максвеллом.

Максвелл предполагал, что газ состоит из большого числа N одинаковых молекул (они находятся в состоянии хаотического теплового движения при одинаковой температуре) и что силовые поля на газ не действуют.

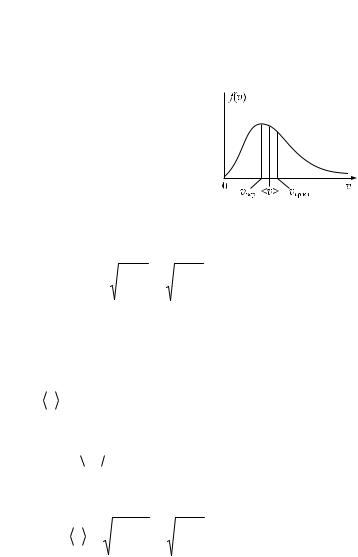
Закон Максвелла определяет некоторую функцию f (v), называемую

функцией распределения молекул по скоростям.

Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), имеющих скорость, заключенную в этом интервале. Функция f (v) определяет относительное число молекул dN (v) /N, скорости которых лежат в интервале [v, v + dv] (èëè вероятность dP того, что скорость молекулы принадлежит данному интервалу):

Вероятность того, что молекула имеет какую-либо скорость, равна

единице:

0

72

Условие (2.24) называют условием нормировки.

Применяя методы теории вероятностей, Максвелл нашел функцию f(v) — закон для распределения молекул идеального газа по скоростям (рис. 2.2):

ãäå k — коэффициент Больцмана; A — константа, найденная из условия нормировки (2.24), бесконечный верхний предел для скорости в котором оправдан ввиду малости подынтегрального выражения для больших скоро-

Средняя скорость молекулы v (средняя арифметическая скорость) и среднее значение квадрата скорости v2 определяется по формулам из теории вероятностей:

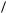v 2 v 2 f (v)dv.

0

Произведя вычисления, можно получить:

73

откуда для средней квадратичной скорости получается соотношение (2.20).

Приведeнные характерные скорости отличаются друг от друга в следующих пропорциях:

vâåð : v : vñð.êâ = 1 : 1,13 : 1,22.

Зная распределение Максвелла по скоростям (2.25), можно, например, оценить число молекул, скорости которых лежат в произвольном интервале [v1, v2]:

ãäå N — общее число молекул.

Барометрическая формула. Распределение Больцмана

При выводе закона Максвелла для распределения молекул идеального газа по скоростям мы предположили, что на молекулы газа внешние силы не действуют. Поэтому можно было считать, что молекулы равномерно распределены по объему сосуда; температура везде одинакова.

На самом деле молекулы газа всегда находятся в поле тяготения Земли. Если бы не было теплового движения, то все молекулы атмосферного воздуха упали бы на Землю, а если бы не было тяготения, то атмосферный воздух рассеялся бы по всей Вселенной. Тяготение и тепловое движение приводят газ в состояние, при котором его концентрация и давление убывают с высотой.

Пусть идеальный газ находится в равновесном состоянии в однородном поле тяготения Земли. Давление газа на высоте h обусловлено весом вышележащих слоев. Обозначим ð давление на высоте h, тогда давление на высоте h + dh равно ð + dp, причем если dh 0, òî dp 0, так как вес вышележащих слоев атмосферы, а следовательно, и давление с высотой убывают. Разность давлений ð è p + dp равна весу газа, заключенному в объеме вертикального цилиндра с площадью основания, равной единице, и высотой dh:

p – (p + dp) = gdh,

где — плотность газа на высоте h. Отсюда

74

dp pg dh, интегрируя которое (полагая T = const) по высоте от 0 до

RT

ãäå ð è ð0 — давления газа на высотах h è h = 0.

Формула (2.31) называется барометрической. Из нее следует, что давление убывает с высотой по экспоненциальному закону.

Барометрическая формула позволяет определять высоту h с помощью барометра. Специально проградуированный барометр для непосредственного отсчета высоты над уровнем моря называют альтиметром. Его широко применяют в авиации, при восхождении на горы.

Преобразуя в выражении (2.31) показатель степени (поделив на число Авогадро), получаем

ãäå mìîëgh = ï — потенциальная энергия молекулы на высоте h.

Ïðè T = const давление p пропорционально концентрации молекул n (см. (2.14)), поэтому можем записать, что:

ãäå n è n0 — концентрации молекул на высотах h 0 è h = 0 соответственно.

Больцман показал, что распределение (2.33) справедливо не только

âпотенциальном поле сил земного тяготения, но и в любом потенциальном поле сил для совокупности любых одинаковых частиц, находящихся

âсостоянии хаотического теплового движения. Поэтому распределение (2.33) называют законом Больцмана.

75

Явления переноса в газах

При отсутствии равновесия в газе всегда имеется пространственная неоднородность тех или иных его параметров — плотности, давления, температуры. Если такой газ предоставить самому себе, то хаотическое движение молекул постепенно выравнивает эти неоднородности и газ приходит в состояние термодинамического равновесия.

Явления выравнивания сопровождаются направленным переносом ряда физических величин: массы, импульса, энергии и т. д.— и поэтому называются явлениями переноса.

К явлениям переноса относятся диффузия (обусловленная переносом массы), теплопроводность (обусловленная переносом энергии) и внутреннее трение èëè вязкость (обусловленная переносом импульса). В основе всех явлений переноса лежит один и тот же механизм: беспорядочность теплового движения молекул газа, непрерывные соударения между ними приводят к постоянному перемешиванию частиц и изменению их скоростей и энергий. Если в газе существует пространственная неоднородность (градиент) плотности, температуры или скорости упорядоченного перемещения отдельных слоев газа, то тепловое движение молекул выравнивает эти неоднородности. Таким образом, явления переноса возникают вследствие наложения хаотического движения молекул окружающей среды на упорядоченное перемещение молекул в отдельных слоях газа.

Диффузия. Диффузия в газе — это процесс перемешивания молекул, сопровождающийся переносом массы из мест с большей концентрацией (плотностью) данных молекул в места с меньшей концентрацией этих молекул. Таким образом, в процессе диффузии переносится масса, а изменяющейся величиной является плотность газа .

Явление диффузии для химически однородного газа подчиняется закону Фика:

ãäå J mx — плотность потока массы вдоль оси x — величина, определяемая массой вещества, диффундирующего в единицу времени через еди-

76

циент диффузии, [D] = ì2/ñ; d — градиент плотности, равный скорости dx

изменения плотности на единицу длины x.

Коэффициент диффузии D численно равен плотности потока массы при единичном градиенте плотности.

Теплопроводность. Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, т. е., иными словами, выравнивание температур.

Перенос энергии (в форме теплоты) подчиняется закону Фурье:

ãäå J Ex — плотность теплового потока вдоль оси x — величина, определяемая энергией, переносимой в единицу времени через единичную

площадку, перпендикулярную оси x: J Ex E ; — коэффициентS' t

теплопроводности, [ ] Âò/(ì·Ê); dT — градиент температуры, равный dx

изменению температуры на единицу длины x.

Коэффициент теплопроводности численно равен плотности теплового потока при единичном градиенте температуры.

Внутреннее трение (вязкость). Вязкость жидкости характеризует те силы внутреннего трения, которые имеют место, когда отдельные слои жидкости движутся с разными скоростями. На рис. 2.3 показаны условно

молекулы жидкости переходят из одного слоя в другой, перенося при этом и импульс упорядоченного движения. При этом импульс упорядо-

77

ченного движения слоя, который движется быстрее, уменьшается, а импульс слоя с меньшей скоростью увеличивается, т. е. слой с большей скоростью тормозится, а слой с меньшей скоростью ускоряется. А это и означает, что между слоями возникают силы внутреннего трения.

Опыт показал, что сила внутреннего трения зависит от величины поверхности слоев S жидкости и от градиента скорости жидкости dvdx (в направлении, перпендикулярном скорости):

Коэффициент пропорциональности называется динамической вязкостью (коэффициентом вязкости жидкости). [ ] = Па·с. Следова-

равен силе внутреннего трения, приходящейся на единицу площади при градиенте скорости, равном единице.

Взаимодействие двух слоев согласно второму закону Ньютона можно рассматривать как процесс, при котором от одного слоя к другому в единицу времени передается импульс, равный по модулю действующей силе. Тогда выражение (2.36) можно представить в виде

ãäå J px — плотность потока импульса вдоль оси x — величина, определяемая полным импульсом, переносимым в единицу времени вдоль оси x

Из сопоставления формул (2.34), (2.35) и (2.37), описывающих явления переноса, следует, что закономерности всех явлений переноса сходны между собой.

Реальные газы. Уравнение Ван-дер-Ваальса

При описании свойств газов мы пользовались моделью идеального газа, молекулы которого не взаимодействуют между собой на расстоянии, и их размерами можно пренебречь.

C увеличением давления и понижением температуры поведение реального газа отличается от поведения идеального газа, так как средние

78

расстояния между молекулами уменьшаются и становится существенным взаимодействие молекул друг с другом. Кроме того, суммарный объем самих молекул становится соизмеримым с объемом сосуда, в котором находится газ.

Из большого числа уравнений, предложенных для описания поведения реальных газов, самым простым и вместе с тем дающим достаточно хорошие результаты, оказалось уравнение голландского физика Ван-дер-Ваальса (1873).

Ван-дер-Ваальс предложил внести поправки к давлению и объему в уравнение Менделеева — Клапейрона (2.11):

ãäå à è b — постоянные Ван-дер-Ваальса, определяемые для каждого конкретного газа опытным путем.

Поправка a к давлению, приводящая к появлению дополнительно-

Vì2

го давления на газ, называемого внутренним давлением, обусловлена действием сил притяжения между молекулами газа, à характеризует силы межмолекулярного притяжения.

Поправка b — это поправка на так называемый недоступный объем, равный учетверенному объему всех молекул.

Для произвольного количества вещества с учетом того, чтоV Vì :

ãäå a a 2 , b b — постоянные Ван-дер-Ваальса для молей. Исходя из уравнения (2.39), можно построить изотермы. Так как

уравнение Ван-дер-Ваальса представляет собой уравнение третьей степени относительно объема V, то оно дает одно или три вещественных значения V в зависимости от p è T.

Графически теоретические изотермы Ван-дер-Ваальса представлены на рис. 2.4, где зависимость p îò V дана для различных температур.

При температуре T и давлениях в пределах от p1 äî p2 уравнение (2.39) имеет три вещественных корня. Различие между тремя вещественными решениями при повышении температуры уменьшается. Начиная

79

с определенной для каждого вещества температуры Têð, при любом давлении вещественным оказывается только одно решение. Температура Têð называется критической (точка К на рис. 2.4).

При температурах выше критической изотермы имеют форму, близкую к гиперболе ðV = const и описывают газообразное состоя-

ние вещества (почти идеальный газ).

При температурах ниже критической

изотермы имеют сложную форму и могут за-

ходить даже в область отрицательных давле-

íèé.

Так ли действительно ведет себя газ? Ответ на этот вопрос дает эксперимент. Для того, чтобы получить изотерму опытным путем,

нужно взять вещество в газообразном состоянии и начать медленно сжимать (в сосуде с поршнем), делая одновременно отсчеты давления и объема, а также следя за тем, чтобы температура вещества оставалась постоянной. Результаты подобных опытов при температуре ниже критической приведены на рис. 2.5. Вначале с уменьшением объема давление газа растет, причем ход изотермы достаточно хоро- шо описывается уравнением Ван-дер-Ваальса.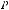

Однако, начиная с некоторого объема Vã, экспериментальная изотерма перестает следовать уравнению (2.39). Начиная с этого значения

объема, давление в сосуде перестает изменяться, само же вещество при этом перестает быть

однородным: часть газа конденсируется в жидкость. Происходит расслоение вещества на две фазы: жидкую и газообразную. По мере дальнейшего уменьшения объема все большая

часть вещества переходит в жидкую фазу, причем переход происходит при постоянном давлении, обозначенном на рис. 2.5 pí.ï. После того как процесс конденсации вещества в жидкость заканчивается (это происходит при достижении объема Væ), дальнейшее уменьшение объема начи- нает сопровождаться быстрым ростом давления. При этом ход изотермы снова примерно следует уравнению Ван-дер-Ваальса (2.39). Вещество в состояниях, соответствующих этому участку, снова будет однородным, но будет представлять собой не газ, а жидкость.

80