Материал презентаций по физике / Лекции для заочников / Физика для гуманитариев_1 / Вотинов_Перминов_Физика

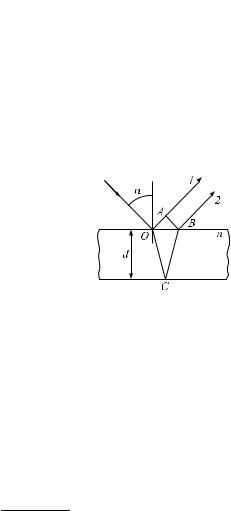
между соседними минимумами интенсивности — шириной интерференционной полосы. Из формул (4.24) и (4.25) следует, что расстояние между полосами и ширина полосы имеют одинаковое значение:

Интерференция света при отражении от тонких пленок

При падении световой волны на тонкую прозрачную пленку или пластинку происходит отражение от обеих поверхностей пленки. В результате возникают две световые волны, которые при известных условиях могут интерферировать.

Пусть на прозрачную плоскопараллельную пластинку падает плоская световая волна, которую можно рассматривать как параллельный пучок лучей. На рис. 4.12 изображен один из лучей этого пучка. Пла-

то волны, представленные этими лучами, когерентны и могут интерферировать. На дальнейшем пути лучей от точек À è Â разность фаз волн 1 è 2 не изменяется. Поэтому оптическая разность хода лучей 1 è 2

ãäå n — показатель преломления пластинки; s2 — суммарная длина отрезков ÎÑ è ÑÂ; s1 — длина отрезка ÎÀ. Показатель преломления среды, окружающей пластинку, полагаем равным единице.

Оптическую разность хода (4.27) можно с учетом закона преломления (4.1) выразить через угол падения :

2d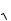n2 sin 2 .

При вычислении разности фаз между колебаниями в лучах 1 è 2 нужно, кроме оптической разности хода, учесть возможность изменения

191

фазы волны при отражении. В точке Î отражение происходит от границы раздела среды, оптически менее плотной, со средой, оптически более плотной. Поэтому фаза волны изменяется на . В точке Ñ отражение происходит от границы раздела среды, оптически более плотной, со средой, оптически менее плотной, так что изменения фазы не происходит. В итоге между лучами 1 è 2 возникает дополнительная разность фаз, равная . Ее можно учесть, добавив к оптической разности хода половину длины волны в вакууме. В результате получим

Если на пути лучей 1 è 2 поставить собирательную линзу, они сойдутся в одной из точек фокальной плоскости линзы и будут интерферировать (роль линзы может играть хрусталик глаза, а роль экрана — сет- чатка). Результат интерференции зависит от значения величины (4.28). Условие максимума (4.20) принимает вид

ãäå m — целое число. При падении под углами, для которых

отраженные волны гасят друг друга, так что свет практически не отражается.

Если на пластинку падает рассеянный (разнообразных направлений) монохроматический свет, то на экране, расположенном в фокальной плоскости линзы, наблюдается чередование светлых и темных полос (кольца с общим центром), соответствующих лучам, падающим на пластинку под определенным углом. Такие интерференционные полосы называются полосами равного наклона.

Если падающий свет немонохроматичен, т. е. содержит диапазон частот (например, белый свет), то интерференционная картина приобретает радужную окраску.

Если монохроматический свет падает на пластинку переменной толщины (например, êëèí), то даже для лучей, падающих под определенным углом, на экране возникнет чередование светлых и темных полос (интерференционная картина). Это объясняется тем, что условие максимума (4.29) выполняется для лучей, падающих на пластинку

192

в местах с определенной толщиной d. Такие полосы называются полосами равной толщины.

Заметим, что интерференция от тонких пленок может наблюдаться

равной толщины имеют вид концентрических окружностей (рис. 4.14), при наклонном падении — эллипсов. Найдем радиусы колец Ньютона в отраженном свете, получающихся при падении света по нормали к пластинке. В этом случае оптическая разность

хода равна удвоенной толщине b зазора (предполагается, что в зазоре n = 1). По рис. 4.13 можно определить, что

R 2 (R b)2 r 2 R 2 2Rb r 2 ,

ãäå R — радиус кривизны линзы; r — радиус окружности, всем точкам которой соответствует

одинаковый зазор b. Ввиду малости b ìû ïðå- Ðèñ. 4.14 небрегли b2 по сравнению с 2Rb. Из этого соот-

ношения следует, что

b r 2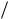2R.

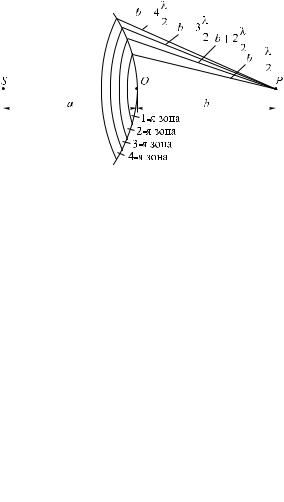
Следовательно, с учетом (4.28) и (4.29) для светлых колец в отраженном свете при нормальном падении лучей получаем (учитывая потерю полуволны при отражении от оптически более плотной среды):

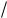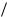2b r 2 R m 12 0 ,

откуда

193

Из (4.30) получаем условие для темных колец (в отраженном свете):

В месте касания пластинки и линзы наблюдается минимум интенсивности, обусловленный изменением фазы на при отражении световой волны от пластинки (оптически более плотной).

4.3. Дифракция

Принцип Гюйгенса — Френеля

Ïîä дифракцией понимают любое отклонение распространения волн вблизи препятствий от законов геометрической оптики (например, огибание волнами встреченных препятствий).

Возникновение дифракции можно объяснить с помощью принципа Гюйгенса, которым устанавливается способ построения фронта волны

в момент времени t + t по известному положе-

нию фронта в момент времени t: каждая точка

фронта волны служит центром (источником)

вторичных волн, а огибающая этих волн дает по-

ложение фронта волны в следующий момент

времени (ðèñ. 4.15).

Пусть на плоскую преграду с отверстием падает параллельный ей фронт волны (рис. 4.16).

По Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта служит центром вторичных волн, которые в однородной и изотроп-

ной среде будут сферическими. Построив огибающую вторичных волн, мы убеждаемся в том, что за отверстием волна проникает в область

геометрической тени (на рис. 4.16 границы этой области показаны пунктиром), огибая края преграды.

Однако принцип Гюйгенса не дает никаких указаний об ам-

194

плитуде, а следовательно, и об интенсивности волн, распространяющихся в различных направлениях. Этот недостаток был устранен Френелем, который дополнил принцип Гюйгенса: вторичные источники (излучающие преимущественно по нормали к фронту волны) когерентны между собой, а новое положение фронта волны — результат интерференции волн от вторичных источников. Иначе говоря, любая волна — результат суперпозиции когерентных вторичных волн, излучаемых фиктивными (вторичными) источниками.

Уточнение Френелем принципа Гюйгенса «стирает» различие между явлениями интерференции и дифракции. Под интерференцией следует понимать суперпозицию когерентных волн от конечного числа источ- ников, а под дифракцией — от бесконечного (распределенных равномерно по некоторой части фронта волны или волновой поверхности).

Различают два вида дифракции. Если источник света и точка наблюдения P расположены от препятствия

настолько далеко, что лучи, падающие на препятствие, и лучи, идущие

в точку P, образуют практически параллельные пучки, говорят о дифракции Фраунгофера èëè î дифракции в параллельных лучах. В противном случае говорят о дифракции Френеля. Дифракцию Фраунгофера можно

наблюдать, поместив за источником света S и перед точкой наблюдения P по линзе так, чтобы точки S è P оказались в фокальной плоскости соответствующей линзы (рис. 4.17).

Зоны Френеля

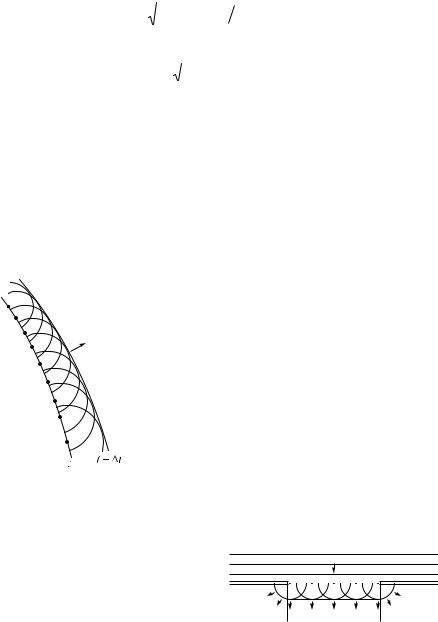
Метод Френеля объясняет прямолинейность распространения света в свободной от препятствий однородной среде. Чтобы показать это, рассмотрим действие сферической световой волны от точечного источника S в произвольной точке пространства Ð (рис. 4.18). Волновая поверхность симметрична относительно прямой SP.

Френель предложил оригинальный метод разбиения волновой поверхности. Она разбивается на кольцевые зоны, построенные так, что расстояния от краев соседних зон до точки P отличаются на /2 ( — длина световой волны в той среде, в которой распространяется волна). Коле-

195

бания, приходящие в точку Ð от аналогичных точек двух соседних зон, противоположны по фазе, так как разность хода от этих зон до точки Ð равна /2. При наложении эти колебания взаимно ослабляют друг друга. Результирующая амплитуда в точке Ð выразится суммой:

Ðèñ. 4.18

Величина амплитуды Àk зависит от площади k-й зоны и угла между внешней нормалью к поверхности зоны и прямой, направленной из этой точки в точку Ð.

Можно показать, что площади всех зон Френеля равновелики и, следовательно, мощности излучения вторичных источников одинаковы. Но с увеличением k возрастает угол между нормалью к поверхности и направлением в точку Ð, что приводит к уменьшению интенсивности излу- чения k-й зоны в данном направлении, т. е. к уменьшению амплитуды Àk по сравнению с амплитудами предыдущих зон. Амплитуда Àk уменьшается также вследствие увеличения расстояния от зоны до точки Ð с ростом номера зоны. В итоге

Вследствие большого числа зон убывание Àk носит монотонный характер и приближенно можно считать, что

196

обнаруживаем, что согласно (4.35) выражения в скобках равны нулю и уравнение (4.33) приводится к виду

Полученный результат означает, что колебания, вызываемые в точке Ð полностью открытой сферической волновой поверхностью, имеют такую же амплитуду, как если бы действовала только половина центральной зоны Френеля. Следовательно, свет от источника S в точку Ð распространяется в пределах очень узкого прямого канала, т. е. прямолинейно.

Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытой только центральную зону Френеля, амплитуда в точке P будет равна A1, т. е. в два раза превзойдет амплитуду (4.37). Соответственно интенсивность в точке P будет в этом случае в четыре раза больше, чем при отсутствии преград между точками S è P.

Пусть волна от источника S встречает на пути непрозрачный экран с круглым отверстием (рис. 4.19, à). Результат дифракции наблюдается на экране, параллельном плоскости отверстия. Дифракционный эффект в точке Ð экрана, расположенной против центра отверстия, зависит от того, сколько зон Френеля укладывается на открытой части волнового фронта. Если в отверстии укладывается ровно k зон Френеля, то амплитуда

Ðèñ. 4.19

197

Если число зон k невелико, то амплитуды колебаний в точке Ð от двух соседних зон мало отличаются по величине, а результат определяется четностью или нечетностью числа k. Если число открытых зон четно, то колебания от соседних зон погашают друг друга и в точке Ð наблюдается минимум интенсивности, если же число зон нечетно, то одна зона оказывается некомпенсированной и в точке Ð наблюдается максимум интенсивности (как от одной зоны). Распределение интенсивности света на экране в случае нечетного числа зон приведено на рис. 4.19, á; в случае четного — на рис. 4.19, â.

При увеличении числа зон k амплитуда Àk стремится к нулю (Àk À1). Никакой интерференционной картины на экране не будет — свет в этом случае практически распространяется так же, как и при отсутствии экрана с отверстием, т. е. прямолинейно. Отсюда следует вывод о том, что следствия волновых представлений и представлений о прямолинейном распространении света начинают совпадать тогда, когда число открытых зон велико.

При размещении между источником S и экраном круглого непрозрач- ного диска закрывается одна или несколько первых зон Френеля. Если диск закроет k зон Френеля, то в точке Ð амплитуда суммарной волны

Так как выражения в скобках можно принять равными нулю (см. (4.35)), получаем:

A Ak 1 . 2

Таким образом, в случае круглого непрозрачного диска в центре картины (точка Ð) при любом (как четном, так и нечетном) k получается светлое пятно.

Если диск закрывает лишь часть первой зоны Френеля, тень на экране отсутствует, освещенность во всех точках такая же, как и при отсутствии преграды. Интенсивность центрального максимума ослабевает при увеличении размеров диска (Ak+1 A1). Если диск закрывает много зон Френеля, интенсивность света в области геометрической тени практически всюду равна нулю и лишь вблизи границ наблюдается слабая интерференционная картина. В этом случае можно пренебречь явлением дифракции и пользоваться законом прямолинейного распространения света.

198

Дифракция Фраунгофера на щели

Пусть плоская монохроматическая волна падает нормально на щель шириной b. Рассмотрим лучи, идущие от вторичных источников на открытой части волновой поверхности под углом(рис. 4.20). Если разность хода от краев щели

равна k , открытую часть волновой поверхности можно разбить на 2k равных по ширине

зон (зон Френеля), причем разность хода от краев каждой зоны равна /2 (рис. 4.21). Коле-

бания, посылаемые в точку наблюдения P соответствующими участками двух соседних зон (например, помеченных крестиками участками зон 1 è 2), находятся в противофазе. Поэтому колебания от каждой пары соседних зон взаимно погашают друг друга и результирующая ам-

плитуда в точке P равна нулю. При = (2k + 1) /2 число зон нечетное,

действие одной из них окажется некомпенси-

рованным, так что будет наблюдаться макси-

мум интенсивности.

С учетом выражения для разности хода от краев щели (см. рис. 4.20)

199

при этом интенсивность второго максимума составляет около 4 % от интенсивности центрального.

Дифракционная решетка

Дифракционной решеткой называется совокупность большого числа одинаковых, отстоящих друг от друга на одно и то же расстояние щелей (рис. 4.23). Расстояние d между серединами соседних щелей называется постоянной èëè периодом решетки.

Ðèñ. 4.23

На дифракционной решетке осуществляется многолучевая интерференция когерентных пучков света, идущих от всех щелей (см. рис. 4.23, à).

Если каждая щель в одном направлении не распространяет свет, то он не будет распространяться и при большем количестве щелей, то есть условие минимума (4.40) для щели справедливо и для решетки.

Разности хода лучей от двух соседних щелей одинаковы в пределах всей дифракционной решетки (см. рис. 4.23, á):

= dsin .

Следовательно, разность фаз

2 2 d sin ,

где — длина волны в данной среде.

Для тех направлений, для которых = 2m, т. е. при условии

200