
Материал презентаций по физике / Лекции для заочников / Физика для гуманитариев_1 / Вотинов_Перминов_Физика
.pdf
I — скорость v. Как будет показано далее, аналогия между электрическими и механическими колебаниями распространяется и на описывающие их математические уравнения.
Найдем уравнение колебаний в контуре без сопротивления. Условимся считать положительным ток, заряжающий конденсатор (рис. 3.38). Тогда 
I |
dq |
. |
(3.147) |
|
|||
|
dt |
|
|
Поскольку сопротивление R контура равно нулю, падения напряжения на соединительных проводах нет и напряжение на конденсаторе1 2 q/Ñ в каждый момент времени равно ЭДС самоиндукции s LdI/dt. Следовательно,
q L dI . C dt
Ðèñ. 3.38
(3.148)
Для изображенной на рис. 3.38 стадии процесса зарядки конденсатора 1 2 положительно, а dI/dt отрицательна (ток уменьшается). Поэтому справа в уравнении (3.148) стоит знак «минус».
Сделав замену dI d 2 q в уравнении (3.148) и произведя простые
dt |
dt 2 |
преобразования, придем к дифференциальному уравнению
d 2 q |
|
1 |
q 0. |
(3.149) |
|
|
|||
dt 2 LC |
|
|||
Получилось уравнение вида (1.92) относительно заряда конденсатора q. Следовательно, заряд на обкладках конденсатора изменяется (колеблется) по гармоническому закону:
q qm cos( 0 t ) |
(3.150) |
||||
с циклической частотой |
|
|
|
|
|
0 |
|
1 |
|
. |
(3.151) |
|
|
|
|||
|
|||||
|
|
LC |
|
||
Эта частота называется собственной частотой контура. Для периода колебаний получается формула Томсона:
161

|
|
|
|
T 2 LC . |
(3.152) |
||
Напряжение на конденсаторе отличается от заряда множителем 1/Ñ:
|
qm |
0 |
|
|
|
m |
0 |
|
|
U |
|
cos |
t |
|
U |
|
cos |
t . |
(3.153) |
C
Продифференцировав функцию (3.150) по времени, получим выражение для силы тока:
m |
|
0 |
0 |
t |
|
I |
m |
0 |
|
I q |
|
sin |
|
|
cos |
t 2 . (3.154) |
Таким образом, сила тока опережает по фазе напряжение на конденсаторе на /2.
Из формул (3.153) и (3.154) следуют выражения для амплитуд напряжения на конденсаторе и силы тока:
U m qm , I m qm 0 .
C
Взяв отношение этих амплитуд и заменив 0 по формуле (3.151), получим соотношение
|
U m |
|
L |
. |
(3.155) |
|
|
||||
|
I m |
C |
|
||
К этой формуле можно прийти также исходя из того, что наибольшее значение энергии электрического поля CU m2 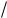 2 равно наибольшему значе- нию энергий магнитного поля LI m2
2 равно наибольшему значе- нию энергий магнитного поля LI m2 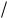 2.
2.
Свободные затухающие колебания
Всякий реальный контур (рис. 3.39) обладает сопротивлением. Энергия, запасенная в контуре, постепенно расходуется в этом сопротивлении на нагревание, вследствие чего свободные колебания затухают. В этом случае ЭДС самоиндукции в каждый момент времени равна сумме напряжения на конденсаторе и напряжения на сопротивлении, равного IR:
|
q |
IR L |
dI |
. |
(3.156) |
||
|
|
|
|||||
C |
|
|
|
dt |
|
||
Введя обозначение |
|
|
|
|
|
|
|
|
|
2 |
R |
, |
(3.157) |
||
|
|
|
|||||
|
|
|
L |
|
|||
162

с учетом (3.151) уравнение (3.156) запишем в виде |
|
||||
|
d 2 q |
2 |
dq |
02 q 0. |
(3.158) |
|
dt 2 |
|
|||
|
|
dt |
|
||
Ñматематической точки зрения уравнение (3.158) тождественно
ñуравнением (1.126). Из сопоставления формул (3.157) и (1.125) следует, что электрическое сопротивление R играет роль коэффициента сопро-
тивления среды r.
В случае, когда 0, решение уравнения имеет вид
0 |
ç |
|
(3.159) |
q q |
e t cos |
t . |
Здесь начальные амплитуда q0 и фаза определяются из начальных условий; циклическая частота затухающих колебаний
ç 
 20 2
20 2 
 1
1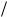 LC R 2
LC R 2 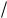 4L2 .
4L2 .
Ðèñ. 3.39
(3.160)
График функции (3.159) изображен на рис. 3.40.
Логарифмический декремент затухания (1.134)
T |
R |
|
2 |
|
R |
. |
(3.161) |
||||
|
|
|
|
|
|||||||
|
|
2L ç L ç |
|
||||||||
Добротность контура (1.136) |
|
||||||||||
Ðèñ. 3.40 |
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
L ç |
. |
(3.162) |
||||||
|
|
||||||||||
|
R |
|
|||||||||
Вынужденные электромагнитные колебания
Чтобы вызвать вынужденные электромагнитные колебания, нужно, разорвав контур, подать на образовавшиеся контакты переменное напряжение (рис. 3.41):
U U 0 cos t. |
(3.163) |
Это напряжение нужно добавить к ЭДС самоиндукции. В результате соотношение (3.156) примет вид
163

|
q |
IR L |
dI |
U 0 cost |
|
||||
|
|
|
|
|
|
||||
C |
|
|
dt |
|
|||||
èëè |
|
|
|
|
|
|
|
|
|
|
|
q |
IR L |
dI |
U 0 cost. |
(3.164) |
|||
|
C |
|
|||||||
|
|
dt |
|
||||||
Отношение q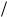 C есть напряжение UC на конденсаторе, произведение IR равно напряжению UR на сопротивлении, выражение LdI
C есть напряжение UC на конденсаторе, произведение IR равно напряжению UR на сопротивлении, выражение LdI dt определяет напряжение UL на индуктивности. Поэтому можно на-
dt определяет напряжение UL на индуктивности. Поэтому можно на-
Ðèñ. 3.41 |
писать, что |
|
|
|
|
|
UC U R U L U 0 cost. |
(3.165) |
Таким образом, сумма напряжений на отдельных элементах контура равна в каждый момент времени напряжению, приложенному извне (см. рис. 3.41).
С учетом введенных ранее обозначений (3.151) и (3.157) уравнение (3.164) перепишем в виде
d 2 q |
2 |
dq |
02 q |
U 0 |
cost. |
(3.166) |
dt 2 |
dt |
|
||||
|
|
L |
|
|||
Это неоднородное (правая часть отлична от нуля) дифференциальное уравнение второго порядка с постоянными коэффициентами. Как известно из теории дифференциальных уравнений, общее решение неоднородного уравнения (3.166) равно сумме общего решения (3.159) однородного уравнения (3.158), соответствующего данному неоднородному, и частного решения данного неоднородного уравнения (которое можно найти по виду правой части):
q q |
m |
sin(t ) q |
m |
|
|
(3.167) |
|
|
cos t 2 . |
||||
Амплитуду заряда qm и отставание по фазе можно найти, непосредственно подставляя частное решение (3.167) в уравнение (3.166), откуда
qm |
|
|
U 0 |
L |
|
|
|
|
|
|
U 0 |
|
|
|
|
, (3.168) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
R 2 L 1 |
|
|
2 |
|||||||
2 |
2 |
2 |
|
2 |
|
|
C |
|
|
||||||||
|
0 |
|
|
4 |
|
|
|
|
|
|
|
|
|
||||
164

|
2 |
02 |
L 1 C |
|
|
|
tg |
|
|
|
|
. |
(3.169) |
|
|
|
||||
|
2 |
R |
|
|
||
Общее решение уравнения (3.166), описывающее изменение заряда конденсатора при вынужденных колебаниях:
q q0e t cos ç t qm cos t  2 .
2 .
Первое слагаемое в этом уравнении играет заметную роль только в начальной стадии процесса, при так называемом установлении колебаний. С течением времени из-за экспоненциального множителя e– t роль этого слагаемого уменьшается, и через некоторое время им можно пренебречь, сохраняя лишь второе слагаемое.
Таким образом, функция (3.167) описывает установившиеся вынужденные колебания. Они представляют собой гармонические колебания с частотой, равной частоте подаваемого напряжения.
Сила тока при установившихся вынужденных колебаниях в контуре меняется по следующему закону:
|
dq |
|
0 |
|
|
|
I |
|
I |
|
cos t , |
(3.170) |
|
dt
где амплитуда тока
I 0 qm |
|
U 0 |
|
|
|
. |
(3.171) |
|
|
|
|
|
|||
|
|
2 |
|||||
|
|
R 2 L 1 C |
|
|
|
|
Ток отстает от внешнего напряжения по фазе на угол , определяемый соотношением (3.169).
Установившиеся вынужденные электрические колебания можно рассматривать как протекание в цепи переменного тока, обладающей емкостью, индуктивностью и сопротивлением.
Полученное выражение для амплитуды силы тока (3.171) можно формально толковать как закон Ома для амплитудных значений тока и внешнего напряжения. Стоящую в знаменателе этого выражения вели- чину, имеющую размерность сопротивления, обозначают буквой Z и называют полным сопротивлением цепи переменного тока:
I 0 |
|
U 0 |
, |
(3.172) |
|
||||
|
|
Z |
|
|
165

Z |
|
|
2 . |
(3.173) |
R 2 L 1 C |
|
Величину, стоящую в круглых скобках этого выражения, обознача- ют X и называют реактивным сопротивлением:
X L 1 C. |
(3.174) |
При этом величину L называют индуктивным сопротивлением, а величину 1/C — емкостным сопротивлением. Их обозначают соответственно XL è XC. Сопротивление R в этом случае называют активным сопротивлением цепи. Термин «активное сопротивление» используется
âтом смысле, что именно на этом сопротивлении рассеивается энергия
âвиде тепла. Итак,
XL L, XC 1/C, X XL – XC, Z 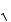
 R 2 X 2 . (3.175)
R 2 X 2 . (3.175)
Найдем напряжения на отдельных элементах контура:
|
|
|
|
|
|
|
|
UC q |
|
||||||
qm cos t 2 |
UCm cos t 2 , (3.176) |
||||||
CC
U |
R |
0 |
|
|
U |
Rm |
|
|
(3.177) |
|
IR I |
R cos t |
|
cos t , |
|||||
U L L dI dt
Ðèñ. 3.42
LI 0 sin t U Lm cos t  2 . (3.178)
2 . (3.178)
Из формул (3.176)–(3.178) видно, что UR находится в фазе с током I (3.170), UC отстает по фазе от I íà /2, à UL опережает I на /2. Все это можно наглядно представить с помощью векторной диаграммы (см. разд. 1.3), изобразив амплитуды напряжений и их векторную сумму, равную согласно (3.165) вектору внешнего напряжения (рис. 3.42).
Резонансную частоту для заряда q и напряжения UC на конденсаторе можно найти аналогично резонансной частоте (1.142) для смещения при механических колебаниях, исследовав функцию (3.168) на максимум:
166

|
|
|
|
1 |
|
R 2 |
|
|
|
ðåçq ðåçUC |
02 2 2 |
. 0 . |
(3.179) |
||||||
LC |
2L2 |
||||||||
|
|
|
|
|
|
|
Резонансные кривые для UC изображены на рис. 3.43, à (резонансные кривые для q имеют точно такой же вид). Резонансные кривые для силы тока изображены на рис. 3.43, á. Амплитуда силы тока (3.171) имеет максимальное значение при
X L 1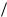 C 0,
C 0,
откуда
|
|
|
|
ðåçI 1 LC 0 . |
(3.180) |
||
Разности потенциалов на индуктивности и емкости имеют при резонансе тока одинаковые амплитуды и противоположные фазы, так что их сумма обращается в нуль, а напряжение на активном сопротивлении оказывается равным ЭДС источника энергии.
Ðèñ. 3.43
На описанном явлении основаны все радиоприемные устройства, неотъемлемой частью которых является колебательный контур с изменяемой резонансной частотой.
Мощность в цепи переменного тока
Мгновенное значение мощности, выделяемой в цепи, равно произведению мгновенных значений напряжения (3.163) и силы тока (3.170):
P(t) U(t)I (t) U 0 cos tI 0 cos t ,
где определяется соотношением (3.169):
167

tg L 1 C X ,
C X ,
R |
R |
||
откуда можно получить |
|
||
cos |
R |
. |
(3.181) |
|
|||
|
Z |
|
|
Воспользовавшись формулой |
|
||
cos cos 1 cos 1 cos ,
22
выражению для мгновенной мощности можно придать вид
P t |
1 |
U 0 I 0 cos |
1 |
U 0 I 0 cos 2t . |
2 |
2 |
Практический интерес представляет среднее по времени значение P(t), которое мы просто обозначим P. Так как среднее значение cos (2t – ) равно нулю,
P |
1 |
U 0 I 0 cos . |
(3.182) |
|
|||
2 |
|
|
|
Если ток в цепи не совершает механической работы, средняя мощность выделяется в активном сопротивлении в виде тепла.
Подставив значение cos (3.181) в (3.182) с учетом (3.172), получим
P |
RI 02 |
. |
(3.183) |
|
|||
2 |
|
|
|
Такую же мощность развивает постоянный ток, сила которого
I ÝÔ |
I |
0 |
|
. |
(3.184) |
|
|
|
|||
2 |
|
|
|
||
Величина IÝÔ называется действующим (эффективным) значением силы тока. Аналогично, величина
U ÝÔ |
U |
0 |
(3.185) |
|
|
||
2 |
|
||
называется действующим (эффективным) значением напряжения. Действующим èëè эффективным значением переменного тока
называется такое значение постоянного тока, при котором на активном
168
сопротивлении выделяется за период такое же количество теплоты, как и при переменном токе. Аналогично и для действующего (эффективного) значения напряжения.
Например, стандартное напряжение в сети 220 В — это эффективное напряжение. По формуле (3.185) легко посчитать, что амплитудное зна- чение напряжения в этом случае будет равно 311 В.
С использованием действующих значений формуле (3.182) для средней мощности можно придать вид
P U ÝÔI ÝÔ cos . |
(3.186) |
В выражение для мощности входит множитель cos (3.181), который называют коэффициентом мощности. В технике стремятся сделать cos как можно больше. При малом cos для выделения в цепи необходимой мощности нужно пропускать ток большей силы. При этом возрастают потери в подводящих проводах, и приходится увеличивать их сечение.
На практике устанавливается предельно допустимое значение cos для предприятия, при достижении которого возможно отключение его от внешней сети (например, при cos ~ 0,85). Для повышения cos необходимо, как видно из векторной диаграммы (см. рис. 3.42), уравнять амплитудные значения напряжения на емкости и индуктивности электри- ческой цепи. Это может потребовать значительных капитальных вложений на переоборудование станочного парка на предприятии, изменение технологии. Быстро повысить cos можно, увеличивая (см. (3.181)) активное сопротивление, подключая нагревательные элементы и осветительное оборудование. Вот почему иногда можно наблюдать картину включения освещения на территории предприятий в дневное время в условиях достаточной видимости.
Электромагнитные волны
Мы знаем, что переменные электрическое и магнитное поля взаимно порождают друг друга: переменное магнитное поле порождает электри- ческое (см. уравнение (3.142)), переменное электрическое поле порождает магнитное (см. уравнение (3.143)). Таким образом, если возбудить с помощью колеблющихся зарядов переменное электромагнитное поле, то в окружающем заряды пространстве возникает последовательность взаимных превращений электрического и магнитного полей, распространяющихся от точки к точке. Этот процесс периодический во времени и в пространстве и, следовательно, представляет собой волну.
169

Из уравнений Максвелла можно получить для векторов напряжен- |
|
|
|
ностей электрического E и магнитного H полей так называемые волновые уравнения (связанные друг с другом), которые в одномерном случае
имеют вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
!2 E |
|
|
!2 E |
|
|||
|
|
2 0 0 |
|
|
, |
||
|
!x |
!t 2 |
|||||
|
|
|
|
|
|
|
(3.187) |
|
!2 H |
0 |
0 |
!2 H |
|
||
|
|
|
|
|
. |
||
|
!x |
2 |
|
|
!t |
2 |
|
|
|
|
|
|
|
||
Всякая функция, удовлетворяющая волновому уравнению, представляет собой волну, причем корень квадратный из величины, обратной коэффициенту при производной по времени, дает фазовую скорость этой волны:
v |
|
1 |
|
|
|
c |
|
, |
(3.188) |
|
|
|
|
|
|
||||
|
|
||||||||
|
|
0 0 |
|
|
|
|
|
||
ãäå c 1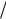

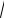 0 0 3 108 м/с — скорость электромагнитных волн в ва-
0 0 3 108 м/с — скорость электромагнитных волн в ва-
кууме. Поэтому Максвелл еще задолго до экспериментального подтверждения существования электромагнитных волн высказал гипотезу, что свет — электромагнитные волны. Впервые экспериментально доказал существование электромагнитных волн Г. Герц в 1888 г., спустя 9 лет после смерти Максвелла.
Простейшими решениями уравнений (3.187) являются функции (уравнения плоской волны):
|
|
m |
|
|
|
|
E |
|
|||
E |
|
cos t kx , |
(3.189) |
||
|
|
|
|
||
|
|
|
|
||
H H m cos t kx , |
|
||||
|
|
|
|
|
|
где циклическая частота волны = 2 , волновое число k  v 2
v 2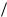 ,
,
— длина волны. Шкала электромагнитных волн, где представлено (упрощенно) условное разбиение по длинам волн на диапазоны радиоволн,
световых волн, рентгеновского è гамма-излучения, имеет следующий вид:
Радиоволны |
Световые волны |
R-излучение |
-излучение |
10–3–10–4 ì |
10–4–10–9 ì |
10–9–6 · 10–12 ì |
6 · 10–12 ì |
170
