
Материал презентаций по физике / Лекции для заочников / Физика для гуманитариев_1 / Вотинов_Перминов_Физика
.pdf
Аналогично, при протекании в контуре 2 òîêà ñèëû I2 возникает сцепленный с контуром 1 поток
#1 L12 I 2 .
При изменениях тока I2, в контуре 1 индуцируется ЭДС
i1 L12 dI 2 .
dt
Контуры 1 è 2 называются связанными, а явление возникновения ЭДС в одном из контуров при изменении силы тока в другом называется
взаимной индукцией.
Коэффициенты пропорциональности L12 è L21 называются взаимной индуктивностью контуров. Соответствующий расчет показывает, что в отсутствие ферромагнетиков эти коэффициенты равны друг другу: L12 = L21. Измеряется взаимная индуктивность также в генри (Гн).
В настоящее время в технике наряду с постоянным током широко используется и переменный ток. Важное преимущество переменного тока над постоянным состоит в том, что напряжение переменного тока можно достаточно легко повышать или понижать практически без потерь энергии с помощью трансформаторов. Трансформаторы — это приборы, при помощи которых преобразуется напряжение переменного тока. Принцип работы трансформаторов основан на законе электромагнитной индукции.
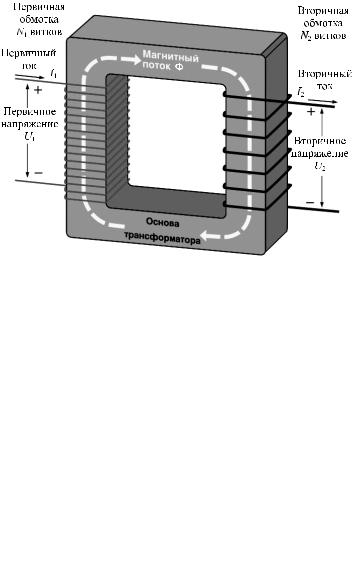
Простейший трансформатор представляет собой две обмотки, навитые на один и тот же ферромагнитный сердечник (рис. 3.35). Концы первой обмотки подключаются к источнику переменного тока с напряжением U1. Эта обмотка называется первичной. К концам второй обмотки, на которых создается переменное напряжение U2, подключается нагрузка, потребляющая электроэнергию. Эта обмотка называется вторичной. Åñëè U2 U1, трансформатор называется повышающим. Если U2 U1, трансформатор называется понижающим.
При подключении первичной обмотки к сети переменного напряжения по ней течет переменный ток, создающий в обмотке переменное магнитное поле и переменный магнитный поток. Все линии магнитного поля, проходящие через витки первичной обмотки, проходят и через витки вторичной обмотки, т. е. поток через один виток вторичной обмотки точно такой же, как поток через один виток первичной обмотки. Это происходит
151
Ðèñ. 3.35
потому, что магнитное поле в ферромагнетиках значительно превышает магнитное поле в воздухе и все замкнутые магнитные силовые линии практически без рассеяния идут внутри общего для обмоток сердечника. Замкнутый ферромагнитный сердечник, являясь «проводником магнитных силовых линий», представляет собой замкнутую «магнитную цепь» — магнитопровод, внутри которого проходят все силовые линии.
В результате электромагнитной индукции переменный магнитный поток в магнитопроводе создает в обеих обмотках ЭДС индукции пропорциональную первой производной магнитного потока. Когда вторич- ная обмотка ни к чему не подключена (режим холостого хода), ЭДС индукции в первичной обмотке практически полностью компенсирует напряжение источника питания, поэтому ток через первичную обмотку невелик. Напряжение на вторичной обмотке в режиме холостого хода определяется коэффициентом трансформации — отношением числа витков первичной обмотки N1 к числу витков вторичной обмотки N2:
K |
U1 |
|
N 1 |
. |
(3.129) |
|
|
||||
U 2 |
|
N 2 |
|
||
При подключении вторичной обмотки к нагрузке по ней начинает течь ток. Этот ток также создает магнитный поток в магнитопроводе,
152
причем он направлен противоположно магнитному потоку, создаваемому первичной обмоткой. В результате в первичной обмотке нарушается компенсация ЭДС индукции и ЭДС источника питания, что приводит к увеличению тока в первичной обмотке до тех пор, пока магнитный поток не достигнет практически прежнего значения. В этом режиме отношение токов первичной и вторичной обмотки равно обратному отношению числа витков обмоток:
I 1 |
|
N 2 |
, |
(3.130) |
|
I 2 |
N 1 |
||||
|
|
|
отношение напряжений в первом приближении остается прежним. В результате мощность, потребляемая от источника в цепи первичной обмотки, практически полностью передается во вторичную.
Наиболее часто трансформаторы применяются в электросетях и в источниках питания различных приборов.
Энергия магнитного поля |
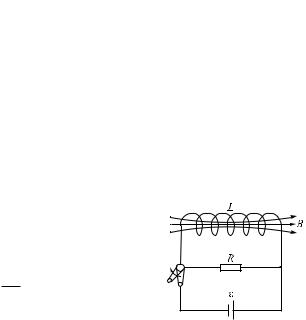
Пусть имеется цепь, изображенная на рис. 3.36. При замкнутом клю- |
че в соленоиде установится ток I, который обусловит магнитное поле, |
сцепленное с витками соленоида. Если разомкнуть ключ, то через сопро- |
тивление R будет некоторое время течь посте- |
пенно убывающий ток, поддерживаемый воз- |
никающей в соленоиде ЭДС самоиндукции. |
Работа, совершаемая током за время dt, |
dA s Idt d Idt Id. (3.131) |
dt |
Эта работа идет на приращение внутренней энергии сопротивления R, обмотки соленоида и соединительных проводов (т. е. на их
нагревание). Совершение работы сопровождается ослаблением магнитного поля. Поскольку никаких других изменений в окружающих электрическую цепь телах не происходит, остается заключить, что магнитное поле является носителем энергии, за счет которой и совершается работа (3.131). Таким образом, обозначив энергию сцепленного с соленоидом магнитного поля через W, можно написать, что
dW dA Id |
(3.132) |
(работа dÀ равна убыли энергии).
153

Если индуктивность соленоида не зависит от |
I (L = const), òî |
d# = LdI и выражение (3.132) принимает вид |
|
dW LIdI . |
(3.133) |
Проинтегрировав это выражение в пределах от 0 до I, получим выражение для энергии магнитного поля соленоида с индуктивностью L, по которому течет ток I:
W |
LI 2 |
. |
(3.134) |
|
|||
2 |
|
|
|
Выразим энергию магнитного поля через величины, характеризующие само поле. В случае бесконечно длинного (практически очень длинного) соленоида
L 0 n2V, H = nI,
откуда
I H . n
Подставляя эти значения L è I в (3.134), получим:
W |
0 H 2 |
V . |
(3.135) |
|
|||
2 |
|
|
|
Магнитное поле бесконечно длинного соленоида однородно и отлично от нуля только внутри соленоида. Следовательно, энергия заклю- чена в пределах соленоида и распределена по его объему с постоянной плотностью w, которую можно получить, разделив W íà V:
w |
0 H 2 |
. |
(3.136) |
|
|||
2 |
|
|
|
С учетом (3.113) выражение для объемной плотности энергии w магнитного поля можно переписать в виде
BH B 2
w . (3.137)
22 0
Данные соотношения получены на примере однородного поля соленоида, но они справедливы и для неоднородного поля.
154

Чтобы найти энергию магнитного поля, заключенную в некотором объеме V, нужно вычислить интеграл
W wdV |
|
0 H 2 |
dV . |
(3.138) |
|
2 |
|||||
V |
|
|
|||
V |
|
|
|||
Уравнения Максвелла
Если неподвижный контур находится в переменном магнитном поле, то согласно открытию Фарадея в контуре возникает индукционный ток, который свидетельствует о том, что изменяющееся во времени магнитное поле вызывает в контуре появление сторонних сил. Эти силы не связаны ни с химическими, ни с тепловыми процессами в проводнике; они также не могут быть магнитными силами, поскольку такие силы работы над зарядами не совершают. Остается заключить, что индукционный ток обусловлен возникающим в проводнике электрическим полем (сторонних сил), причем циркуляция напряженности поля сторонних сил дает ЭДС индукции:
i |
|
|
|
E |
ñò d . |
(3.139) |
Данное выражение для ЭДС является обобщением соотношения (3.64) на случай замкнутого контура.
Согласно закону Фарадея (3.119) можем записать:
i |
d |
|
d |
Bn dS. |
(3.140) |
|
dt |
dt |
|||||
|
|
S |
|
Приравняв правые части формул (3.139) и (3.140), придем к соотношению
|
|
|
|
||
E |
ñò d |
d |
Bn dS. |
(3.141) |
|
dt |
|||||
|
|
S |
|
||
Максвелл предположил, что изменяющееся со временем магнитное поле обусловливает появление в пространстве электрического поля независимо от присутствия в этом пространстве проводящего контура. При- чем это поле существенно отличается от порождаемого неподвижными
155

зарядами электростатического поля. Электростатическое поле потенциально, его линии напряженности начинаются и оканчиваются на зарядах. Циркуляция напряженности электростатического поля по любому замкнутому контуру равна нулю (см. (3.10)). Циркуляция напряженности поля, обусловленного изменяющимся магнитным полем, согласно (3.141) отлична от нуля. Следовательно, это поле, как и магнитное, является вихревым. Линии напряженности вихревого электрического поля замкнуты или уходят в бесконечность.
Итак, электрическое поле может быть как потенциальным, так и вихревым. В общем случае электрическое поле складывается из электростатического поля, создаваемого зарядами, и вихревого поля, обусловленного изменяющимся со временем магнитным полем. Из соотношений (3.10) и (3.141) получаем обобщенную теорему о циркуляции напряженности электрического поля:
|
|
|
|
||
E |
d |
d |
Bn dS, |
(3.142) |
|
dt |
|||||
|
|
S |
|
||
ãäå E — результирующая напряженность электростатического и вихревого электрических полей.
Таким образом, электрическое поле существует не только вокруг зарядов, но и порождается переменным магнитным полем. Рассуждая подобным образом, Максвелл пришел к выводу, что магнитное поле, в свою очередь, порождается не только током, но и переменным электри- ческим полем. Он «поправил» теорему о циркуляции (3.109) следующим образом:
 H d
H d
I i |
d D |
. |
(3.143) |
|
|||
i |
dt |
|
|
Величина D Dn dS представляет собой поток вектора электри-
S
ческого смещения D через поверхность S, ограниченную контуром . Величина d D  dt есть скорость изменения этого потока, которую Максвелл назвал током смещения:
dt есть скорость изменения этого потока, которую Максвелл назвал током смещения:
I ñì |
d D |
|
d |
Dn dS. |
(3.144) |
|
dt |
dt |
|||||
|
|
S |
|
156

Уравнение (3.143) можно записать в виде
|
|
|
H |
d I i I ñì . |
(3.145) |
i
Таким образом, циркуляция вектора напряженности магнитного
поля H по некоторому контуру равна алгебраической сумме макроскопических токов и тока смещения, охватываемых контуром.
Ток смещения — воображаемый ток. Это удобная модель явления, поскольку мы привыкли к тому, что магнитные поля создаются движущимися зарядами или токами. Нам проще считать, что источником некоторого дополнительного магнитного поля является не переменное электрическое поле, а некоторый ток смещения, дополнительный к обычным токам проводимости. Итак, теперь мы можем сказать, что в присутствие переменных электрических полей текут токи смещения, которые порождают магнитное поле, наряду с токами проводимости.
Открытие тока смещения позволило Максвеллу создать единую теорию электрических и магнитных явлений. Эта теория объяснила все известные в то время экспериментальные факты и предсказала ряд новых явлений, существование которых подтвердилось впоследствии.
Основу теории образуют четыре уравнения Максвелла. В учении об электромагнетизме эти уравнения играют такую же роль, как законы Ньютона в механике или основные законы (начала) в термодинамике.
Первую пару уравнений Максвелла образуют уравнения (3.142) и (3.102):
|
|
|
||
E |
d |
d |
Bn dS, |
|
dt |
||||
|
|
S |
||
 Bn dS 0.
Bn dS 0.
S
Первое из этих уравнений связывает значения E с изменениями век-
òîðà B во времени и является, по существу, выражением закона электромагнитной индукции. Второе уравнение указывает на отсутствие источ- ников магнитного поля, т. е. магнитных зарядов.
Вторую пару уравнений Максвелла образуют уравнения (3.143) и (3.39):
|
|
d |
|
|
H |
d I i |
Dn dS, |
||
|
||||
|
i |
dt |
||
|
|
S |
||
157
 Dn dS q.
Dn dS q.
S
Первое уравнение устанавливает связь между токами проводимости
и смещения и порождаемым ими магнитным полем. Второе уравнение
показывает, что источниками вектора D служат сторонние заряды.
Отметим, что в первую пару уравнений входят только основные ха-
рактеристики поля: E è B. Во второй же паре фигурируют только вспомо- |
|||
|
|
|
|
гательные величины: D è H . |
|
|
|
Для описания полей в изотропных средах к системе нужно добавить |
|||
|
|
|
|
уравнения связи между векторами E è D, B è H (ñì. (3.37) è (3.113)): |
|||
|
|
|
|
D 0 E, |
B 0 H . |
||
Существование взаимосвязи между электрическим и магнитным полями указывает на то, что раздельное рассмотрение электрического и магнитного полей имеет лишь относительный смысл. Действительно, чисто электрическое поле создается системой неподвижных зарядов. Однако если заряды неподвижны относительно некоторой инерциальной системы отсчета, то относительно других инерциальных систем эти заряды движутся и, следовательно, порождают не только электрическое, но и магнитное поле. Неподвижный провод с постоянным током создает постоянное магнитное поле. Однако относительно других инерциальных систем этот провод движется. Поэтому создаваемое им магнитное поле в любой точке будет изменяться и, следовательно, порождать вихревое электрическое поле. Таким образом, поле, которое относительно некоторой системы отсчета оказывается чисто электрическим или чисто магнитным, относительно других систем отсчета представляет собой совокупность электрического и магнитного полей, образующих единое электромагнитное поле.
Одним из самых важных выводов, вытекающих из системы уравнений Максвелла, является вывод о возможности существования магнитного и электрического полей, не связанных с какими-то материальными источниками-зарядами. Электрическое и магнитное поля, порождая друг друга, могут распространяться в пространстве. Распространение электромагнитного возмущения называется электромагнитной волной. Радиоволны, видимый свет, инфракрасное, ультрафиолетовое, рентгеновское излучения, -излучение — все эти явления представляют собой
158
электромагнитные волны, отличающиеся частотами колебаний полей и длинами волн. Скорость распространения электромагнитных волн в вакууме (скорость света) c = 3 · 108 м/с. Она выражается через электри- ческую и магнитную постоянные (что само по себе указывает на электромагнитную природу света):
c |
|
1 |
|
. |
(3.146) |
|
|
|
|
||||
0 0 |
||||||
|
|
|
|
|
3.4. Электромагнитные колебания и волны
Колебательный контур
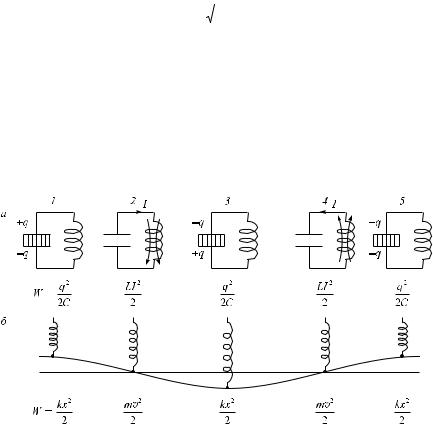
Электрические колебания могут возникать в цепи, содержащей индуктивность и емкость. Такая цепь называется колебательным контуром. На рис. 3.37, à изображены последовательные стадии колебательного процесса в идеализированном контуре с электрическим сопротивлением, равным нулю.
Ðèñ. 3.37
Для того чтобы вызвать колебания, можно присоединить отключенный от индуктивности конденсатор к источнику тока, вследствие чего на обкладках возникнут разноименные заряды величиной qm (позиция 1 íà ðèñ. 3.37, à). Между обкладками возникнет электрическое поле, энергия
159
которого равна q2 2C (см. (3.57)). Если затем отключить источник то-
2C (см. (3.57)). Если затем отключить источник то-
ка и замкнуть конденсатор на индуктивность, емкость начнет разряжаться и в контуре потечет ток. В результате энергия электрического поля будет уменьшаться, зато возникнет все возрастающая энергия магнитного поля, обусловленная током, текущим через индуктивность. Эта энергия равна LI 2  2 (ñì. (3.134)).
2 (ñì. (3.134)).
Так как сопротивление цепи равно нулю, полная энергия, складывающаяся из энергии электрического поля и энергии магнитного поля, не расходуется на нагревание и будет оставаться постоянной. Поэтому в момент, когда напряжение на конденсаторе, а следовательно, и энергия электрического поля обращаются в нуль, энергия магнитного поля, а значит,
èток достигают наибольшего значения (позиция 2; начиная с этого момента ток течет за счет ЭДС самоиндукции). В дальнейшем ток уменьшается и, когда заряды на обкладках достигают первоначальной величины qm, сила тока становится равной нулю (позиция 3). Затем те же процессы протекают в обратном порядке (позиции 4 è 5), после чего система приходит в первоначальное состояние (позиция 5) и весь цикл повторяется снова и снова. В ходе описанного процесса периодически изменяются (т. е. колеблются) заряд q на обкладках, напряжение U на конденсаторе и сила тока I, текущего через индуктивность. Колебания сопровождаются взаимными превращениями энергий электрического и магнитного полей.
Íà ðèñ. 3.37, á колебаниям в контуре сопоставлены колебания пружинного маятника. Сообщению зарядов обкладкам конденсатора соответствует выведение маятника внешней силой из положения равновесия
èсообщение ему первоначального отклонения xm. При этом возникает потенциальная энергия упругой деформации пружины, равная kxm2 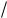 2
2
(см. (1.94)). Позиция 2 соответствует прохождению маятника через положение равновесия. В этот момент квазиупругая сила равна нулю и маятник продолжает двигаться по инерции. К этому времени энергия маятника полностью переходит в кинетическую mv 2 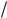 2.
2.
Из сопоставления электрических и механических колебаний следует, что энергия электрического поля аналогична потенциальной энергии упругой деформации, а энергия магнитного поля аналогична кинетиче- ской энергии. Индуктивность L играет роль массы, а величина, обратная емкости (1/Ñ) — роль коэффициента жесткости k. Наконец, заряду q соответствует смещение маятника из положения равновесия õ, à ñèëå òîêà
160
