
Материал презентаций по физике / Лекции для заочников / Физика для гуманитариев_1 / Вотинов_Перминов_Физика
.pdf
!m1v1x m2 v2x m1 u1x m2 u2x ; |
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
2 |
|
"m1v1 |
|
m2 v2 |
|
m1 u1 |
|
m2 u2 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|||||
|
2 |
|
2 |
|
2 |
|
2 |
|
# |
|
|
|
|
||||
Решив систему, можно получить:
u1x |
|
(m1 m2 )v1x 2m2 v2x |
; |
||
|
|
||||
|
|
|
m1 m2 |
||
u2x |
|
(m2 m1 )v2x 2m1v1x |
. |
||
|
|||||
|
|
|
m1 m2 |
||
Пример 2. Центральный абсолютно неупругий удар двух шаров (см. рис. 1.19).
Выполняется закон сохранения импульса:
m1v1x m2 v2x (m1 m2 )ux ,
откуда
ux m1v1x m2v2x .
(m1 m2 )
Изменение механической энергии системы двух шаров
|
|
|
|
|
|
|
m1 |
m2 |
u 2 |
|
|
|
v |
2 |
|
|
m2 |
v |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
|
1 |
|
|
|
2 |
|
|||||
W Wê |
2 |
Wê |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
m1 m2 |
|
|
|
v1 v2 |
2 |
0. |
|
|
|
|
|
|
|||||||
|
|
2 m m |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Аналогия в динамике
Аналогию в динамике поступательного и вращательного движений можно проследить по табл. 1.3.
|
|
Ò à á ë è ö à 1 . 3 |
|
|
|
|
|
Поступательное движение |
Вращательное движение |
||
|
Физические величины |
|
|
Масса, кг |
m |
Момент инерции, кг·м2 |
Iz |
Ñèëà, Í |
|
Момент силы, Н·м |
|
F, Fx |
MO , Mz |
||
|
|
Момент импульса, кг·м2/ñ |
|
Импульс, кг·м/с |
p, px |
LO , Lz |
|
31

|
|
|
|
|
|
|
|
Î ê î í ÷ à í è å ò à á ë . 1 . 3 |
|||||||
|
|
|
|||||||||||||
Поступательное движение |
|
Вращательное движение |
|||||||||||||
|
|
|
|
|
|
|
Законы изменения для системы |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
dp |
|
|
|
|
|
|
|
|
|
||||
|
|
|
Fi e |
|
|
dLO |
|
||||||||
|
|
|
|
|
MOe i |
||||||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
dt |
|
i |
|
|
|
dt |
|
i |
|||||
|
dpx |
Fixe |
|
|
|
dLz |
Mzei |
||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
dt |
|
i |
|
|
|
dt |
|
i |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
Основное уравнение для тела |
|
|
|
|||||
maCx Fixe |
|
|
Iz z Mzei |
||||||||||||
|
|
|
|
|
|
i |
|
|
|
|
|
|
i |
||
|
|
|
|
|
|
|
|
Работа, Дж |
|
|
|
|
|
|
|
|
|
A F s |
|
|
|
A Mz |
|||||||||
|
|
|
|
|
|
|
|
Мощность, Вт |
|
|
|
||||
|
|
N F v |
|
|
|
N Mz |
|||||||||
|
|
|
|
|
|
|
Кинетическая энергия, Дж |
|
|
|
|||||
|
|
Wê |
|
mv2 |
|
|
|
|
Wê |
Iz 2 |
|
||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
||
1.3. Колебательное движение
Характеристики колебаний
Колебаниями èëè колебательными движениями называются движения или процессы, обладающие той или иной степенью повторяемости во времени. Например, механические колебания тела, подвешенного на пружине, качание маятников, колебания струны, вибрации, электромагнитные колебания и др.
Разнообразные по природе, колебания могут иметь общие закономерности и описываться однотипными математическими методами.
Периодические колебания — колебания, при которых значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени. Например, положение маятника в ча- сах, абсолютное значение силы тока в сети переменного тока.
Периодом колебаний T называется наименьший промежуток времени, по истечении которого повторяются значения всех величин, характеризующих колебательное движение. [T] = ñ.
32

Частота — число колебаний в единицу времени. Единица частоты — ãåðö: [ ] = Гц. Частота — величина, обратная периоду:
1. T
Циклическая (круговая) частота — число колебаний за 2 единиц времени, [ ] = рад/с:
= 2 .
Частным случаем периодических колебаний являются гармониче- ские колебания — колебания, совершающиеся по закону синуса или косинуса.
Пусть некоторая материальная точка совершает гармоническое колебательное движение около положения равновесия вдоль некоторой оси x. В этом случае ее координата меняется по закону:
x Acos(t ).
Координату материальной точки x называют смещением из положения равновесия. A = xmax — амплитуда колебаний, = t + — фаза колебаний, — начальная фаза. Значения величин A и определяются из начальных условий в каждом конкретном случае. Циклическая частота является характеристикой колебательной системы.
Система, совершающая гармонические колебания около положения равновесия, называется гармоническим осциллятором.
Простейшей моделью гармонического колебания является колебание проекции x конца радиуса-вектора r точки, движущейся по окружности радиуса A с постоянной угловой скоростью 0 (рис. 1.20). Такое представление гармонических колебаний называют векторной диаграммой. Угол поворота меняется 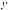
по закону равномерного вращения: = 0t + . Проекция же конца радиуса-вектора точки меняется по гармоническому закону:
0 |
|
(1.89) |
|
x Acos |
t . |
|
|
Свободными называются такие колебания, |
|
||
которые происходят в системе, не подвержен- |
|
||
ной действию переменных внешних сил. При- |
Ðèñ. 1.20 |
||
33
мером могут служить колебания маятника, однократно выведенного из положения равновесия.
Если система консервативна, то в ней не происходит рассеяния энергии (диссипации).
Незатухающие колебания — колебания, происходящие в консервативной системе.
Скорость при гармонических колебаниях
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
v |
x |
|
|
A |
0 |
sin |
t |
|
v |
max |
cos |
t |
|
, (1.90) |
|
|
|||||||||||||
|
|
|
dt |
|
|
|
|
|
|
|
|
|
2 |
|
ãäå A 0 vmax — амплитуда скорости. Из сравнения (1.89) и (1.90) сле-
дует, что скорость опережает смещение по фазе на (рис. 1.21). 2
Ускорение при гармонических колебаниях
Ðèñ. 1.21 |
ax |
dvx |
|
d 2 x |
|
|
|
|
dt |
|
|
|
||||
|
|
dt 2 |
|
|
|
||
0 |
0 |
|
|
(1.91) |
|||
A 2 cos |
t |
|
|||||
20 x
amax cos 0 t ,
ãäå A 20 amax — амплитуда ускорения. Из сравнения (1.89) и (1.91) следует, что ускорение опережает смещение по фазе на , т. е. ускорение и смещение меняются в противофазе (см. рис. 1.21).
Из уравнения (1.91) также видно, что ax 20 x èëè
d 2 x |
02 x 0. |
(1.92) |
|
||
dt 2 |
|
|
Соотношение (1.92) называют дифференциальным уравнением колебаний (свободных незатухающих). Функция (1.89) является решением этого уравнения.
34

Определим силу, под действием которой происходят гармонические колебания тела массой m вдоль оси x. По второму закону Ньютона с уче- том (1.91)
Fx max m 02 x kx. |
(1.93) |
Силы типа (1.93), пропорциональные смещению тела из положения равновесия, независимо от их природы называют квазиупругими. Коэффициент пропорциональности k m 20 называют коэффициентом квазиупругой силы. Под действием квазиупругой силы типа (1.93) тело будет совершать гармонические колебания по закону (1.89).
Квазиупругая сила обусловливает наличие у тела потенциальной энергии
Wï |
kx2 |
|
kA |
2 |
cos2 |
t . |
(1.94) |
|
|
|
|||||
2 |
2 |
|
0 |
|
|
||
|
|
|
|
||||
Колеблющееся тело обладает также кинетической энергией
Wê mv 2 |
mA2 02 |
sin 2 0 t . |
(1.95) |
|||
|
|
|
|
|
|
|
2 |
2 |
|
||||
|
|
|
||||
Механическая энергия (энергия колебаний)
W Wê Wï |
kA |
2 |
|
mvmax2 |
|
mA2 02 |
. |
(1.96) |
|
|
|
|
|||||
2 |
|
2 |
2 |
|
|
|||
Маятники
Маятник — твердое тело, способное совершать колебания вдоль или вокруг некоторой неподвижной оси.
Пружинный маятник — тело, прикрепленное к пружине и способное совершать колебания вдоль некоторой оси.
Если такой маятник находится в поле силы тяжести, то в положении равновесия удлинение пружины отлично от нуля: x = (рис. 1.22), сила тяжести уравновешивается силой упругости:
mg = k. |
(1.97) |
Второй закон Ньютона для маятника, отклоненного из положения равновесия, с учетом (1.97):
max mg Fóïðx mg k x kx.
35
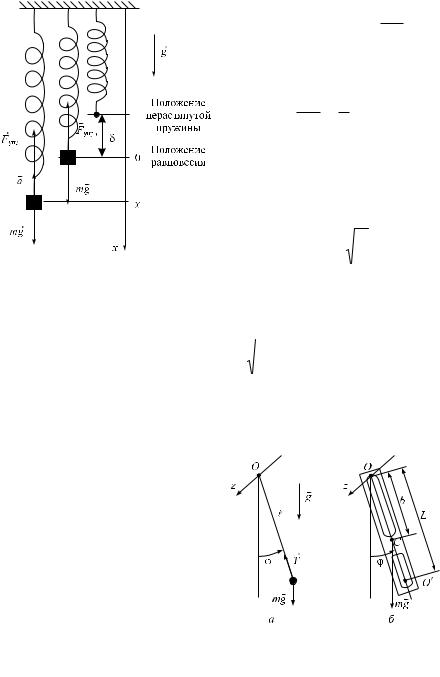
Ðèñ. 1.22 |
Учитывая, что ax d 2 x, ïðè- dt 2
ходим к дифференциальному уравнению колебаний пружинного маятника:
d 2 x k x 0. (1.98) dt 2 m
Получено уравнение типа (1.92), где 0 — циклическая частота колебаний пружинного маятника (собственная частота колебаний),
0 |
|
k |
. |
(1.99) |
|
||||
|
|
m |
|
|
Решением этого уравнения является функция (1.89). Период ко-
лебаний пружинного маятника |
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
T |
2 |
m |
. |
(1.100) |
|||
|
|
||||||
|
0 |
k |
|
||||
Математический маятник — идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешено тело, масса которого сосредоточена в одной точке и которое может совер-
шать колебания под действием силы тяжести.
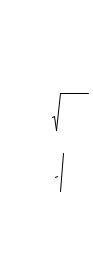
Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити (рис. 1.23, à).
Момент инерции шарика мас-
ñîé m на нити длиной относительно горизонтальной оси z, проходя-
щей через точку подвеса,
36

I z m 2 .
Отклонение маятника от положения равновесия (при колебаниях вокруг горизонтальной оси z) будем характеризовать углом , образованным нитью с вертикалью. Возникающий при этом момент силы тяжести стремится вернуть систему в положение равновесия (его действие аналогично действию квазиупругой силы (1.93)):
M z mg sin ,
где sin — плечо силы тяжести.
Применим основное уравнение динамики вращательного движения (1.65) для маятника, отклоненного из положения равновесия (см. рис. 1.23, à):
I z M z ,
èëè
m 2 mg sin .
Ограничившись рассмотрением малых колебаний, можно положить
sin . С учетом того, что d 2 , приходим к дифференциальному dt 2
уравнению колебаний математического маятника:
d 2 |
|
g |
|
|
|
|
|
0. |
(1.101) |
dt 2 |
|
|||
|
|
|
||
Получено уравнение типа (1.92) относительно угла поворота (углового смещения):
d 2 |
02 0, |
(1.102) |
|
||
dt 2 |
|
|
ãäå 0 — циклическая частота колебаний математического маятника,
0 |
g |
. |
(1.103) |
|||
|
|
|||||
|
|
|
||||
Период колебаний |
|
|
|
|
|
|
|
|
|
|
|
|
|
T 2 |
|
|
. |
(1.104) |
||
|
|
|||||
|
|
g |
|
|||
37
Решением уравнения (1.102) является функция |
|
max cos( 0 t ), |
(1.105) |
ãäå max и определяются из начальных условий.
Физический маятник — твердое тело, способное под действием силы тяжести совершать колебания вокруг неподвижной оси, не проходящей через его центр масс (рис. 1.23, á).
Применим основное уравнение динамики вращательного движения (1.65) для маятника, отклоненного из положения равновесия:
I z mgbsin ,
ãäå Iz — момент инерции тела относительно горизонтальной оси z, проходящей через точку подвеса; b — расстояние от точки подвеса до центра масс; bsin — плечо силы тяжести.
Рассматривая только малые отклонения (sin ), приходим к дифференциальному уравнению колебаний физического маятника:
d 2 |
|
mgb |
|
|
|
|
|
0. |
(1.106) |
dt 2 |
|
|||
|
I z |
|
||
Получено уравнение типа (1.102) относительно угла поворота (углового смещения), решением которого является функция (1.105). При этом0 — циклическая частота колебаний физического маятника,
0 |
mgb |
. |
(1.107) |
|||
|
|
|||||
|
|
I z |
|
|||
Период колебаний |
|
|
|
|
|
|
|
|
|
|
|
|
|
T 2 |
|
I z |
. |
(1.108) |
||
|
|
|||||
 mgb
mgb
Из сопоставления формул (1.104) и (1.108) получается, что математический маятник с длиной нити
L |
I z |
(1.109) |
|
mb |
|||
|
|
будет иметь такой же период колебаний, как и данный физический маятник. Величину L называют приведенной длиной физического маятника. Таким образом, приведенная длина физического маятника L — это длина
38
такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.
Точка на прямой, соединяющей точку подвеса с центром масс, удаленная на расстояние приведенной длины от оси вращения, называется центром качания физического маятника (см. рис. 1.23, á, ò. O).
По теореме Штейнера момент инерции маятника может быть представлен в виде
I z I zC mb 2 , |
(1.110) |
ãäå I zC — момент инерции тела относительно оси, проходящей через центр масс и параллельной оси вращения z; b — расстояние между осями.
Подставив (1.110) в (1.109), получаем
L |
I zC |
b, |
(1.111) |
|
mb
откуда следует, что L b, так что точка подвеса и центр качания лежат по разные стороны от центра масс. Если маятник подвесить за центр кача- ния O , то период колебаний не изменится.
Сложение колебаний одинакового направления и одной частоты
На практике часто приходится иметь дело с таким движением, при котором тело участвует одновременно в двух или нескольких колебаниях. Например, если груз подвешен на пружине к потолку вагона, то груз совершает колебания относительно точки подвеса, которая, в свою очередь, колеблется на рессорах вагона. Таким образом, груз совершает движение, складывающееся из двух колебаний одного направления.
Пусть тело участвует одновременно в двух гармонических колебаниях одной частоты 0:
x1 A1 cos( 0 t 1 ), (1.112) x2 A2 cos( 0 t 2 ).
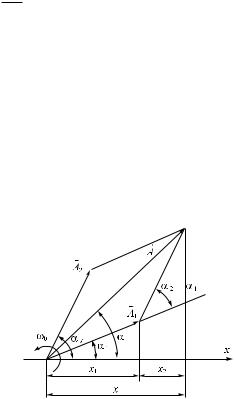
Представим оба колебания
с помощью векторов A1 è A2 íà
векторной диаграмме (рис. 1.24). |
Ðèñ. 1.24 |
39

Построим по правилам сложения векторов результирующий вектор A. Проекция этого вектора на ось õ равна сумме проекций слагаемых векторов:
õ = õ1 + õ2.
Следовательно, вектор A представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью 0, что и векторы A1 è A2 , так что результирующее движение будет гармоническим колебанием с частотой 0, амплитудой À и начальной фазой :
|
|
|
|
0 |
t |
|
|
|
(1.113) |
|
|
|
x Acos |
. |
|
|
|||||
Из построения можно получить: |
|
|
|
|
|
|
|
|||
A2 A2 |
A2 |
2A A |
cos |
1 |
|
; |
||||
1 |
2 |
1 |
|
2 |
|
2 |
||||
tg |
A1 sin 1 |
A2 |
sin 2 |
|
|
|
(1.114) |
|||
. |
|
|
|
|||||||
A1 cos 1 |
A2 |
|
|
|
|
|||||
|
cos 2 |
|
|
|
||||||
Проанализируем выражение (1.114) для амплитуды:
1)если разность фаз обоих колебаний 2 – 1 = 0, то амплитуда результирующего колебания À = À1 + À2;
2)åñëè 2 – 1 = , т. е. оба колебания находятся в противофазе, то
À = |À1 |
– À2|. |
|
Если частоты колебаний õ1 è õ2 неодинаковы, векторы A1 è A2 будут
вращаться с различной скоростью. В этом случае результирующий век-
òîð A пульсирует по величине и вращается с непостоянной скоростью. Результирующим движением в этом случае будет не гармоническое колебание, а некоторый сложный процесс.
Биения
Особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления имеют одинаковую амплитуду и мало отличаются по частоте. Результирующее движение при этих условиях можно рассматривать как гармонические колебания с пульсирующей амплитудой. Такие колебания называются биениями.
Поскольку частоты колебаний несколько отличны, всегда можно выбрать начало отсчета времени так, чтобы начальные фазы обоих коле-
40
