Материал презентаций по физике / Лекции для заочников / Физика для гуманитариев_1 / Вотинов_Перминов_Физика

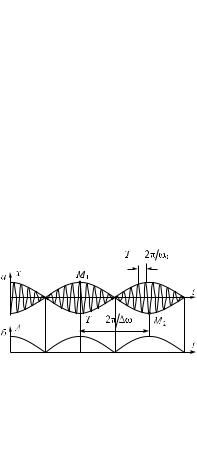
баний были равны нулю. Складываемые колебания в этом случае можно представить в следующем виде:

ïðè ýòîì 0 .

Складывая эти выражения и применяя тригонометрическую формулу для суммы косинусов, получим

График функции (1.116) представлен на рис. 1.25, à. График построен для случая / = 10.

Заключенный в скобки множитель в формуле (1.116) изменяется гораздо медленнее, чем второй множитель. Вследствие условия 0 ,

ну. График амплитуды показан на рис. 1.25, á. Амплитуда — величина положительная, поэтому выраже-

ние для результирующей амплитуды, очевидно, имеет вид

Выражение (1.117) является периодической функцией с частотой, в 2 раза превышающей частоту выражения, стоящего под знаком модуля, т. е. с частотой . Таким образом, частота пульсаций амплитуды — ее называют частотой биений — равна разности частот складываемых колебаний.

41

Сложение взаимно перпендикулярных колебаний

Примером сложения колебаний различного направления является движение следа пучка электронов на экране электронно-лучевой трубки (например, осциллографа) под действием на пучок двух взаимно перпендикулярных переменных электрических полей.

Рассмотрим результат сложения двух взаимно перпендикулярных гармонических колебаний одной частоты 0, происходящих вдоль координатных осей x è y. Если возбудить оба колебания, то материальная точ- ка будет двигаться по некоторой, вообще говоря, криволинейной траектории, форма которой зависит от разности фаз обоих колебаний.

Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний запишутся следующим образом:

где — разность фаз складываемых колебаний.

Выражение (1.118) представляет собой заданное в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Исключив из этих уравнений параметр времени t, можно получить уравнение траектории в неявном виде:

Из аналитической геометрии известно, что уравнение (1.119) есть уравнение эллипса, оси которого ориентированы относительно координатных осей x è y определенным образом.

Ориентация эллипса и величина его полуосей зависят довольно сложным образом от амплитуд À è Â и разности фаз .

Исследуем форму траектории в некоторых частных случаях.

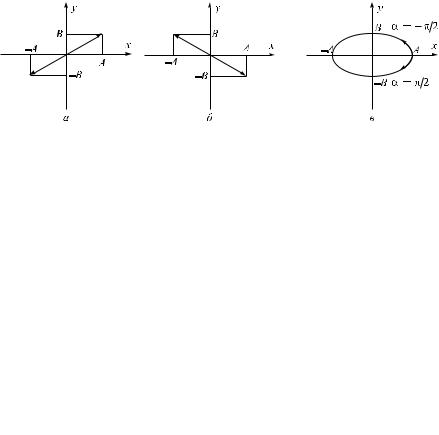
1.= 0. В этом случае уравнение (1.119) принимает вид

2

x y

0,

A B

откуда получается уравнение прямой (рис. 1.26, à):

42

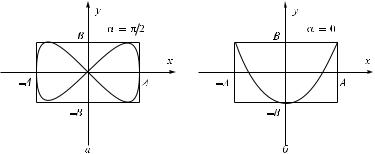
3. = /2. Уравнение (1.119) переходит в уравнение эллипса (рис. 1.26, â):

приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд эллипс вырождается в окружность.

Случаи 2 è 2 отличаются направлением движения по эллипсу или окружности.

Из сказанного следует, что равномерное движение по окружности радиусом R с угловой скоростью 0 может быть представлено как сумма двух взаимно перпендикулярных колебаний:

43

(знак «+» в выражении для y соответствует движению против часовой стрелки, знак «–» — движению по часовой стрелке).

В случае, когда частоты взаимно перпендикулярных колебаний отличаются на очень малую величину , их можно рассматривать как колебания одинаковой частоты, но с изменяющейся разностью фаз. Результирующее движение в этом случае происходит по медленно видоизменяющейся кривой, которая последовательно принимает форму, отвечающую всем значениям разности фаз от – до +.

Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектория результирующего движения может имеет вид довольно сложных кривых, называемых фигурами Лиссажу. На рис. 1.27 показана одна из простейших траекторий, получающаяся при отношении частот 1 : 2, разности фаз, равной /2 (à) è íóëþ (á).

Ðèñ. 1.27

Уравнения колебаний имеют следующий вид:

x Acos 0 t,

y B cos(2 0 t ).

За то время, пока вдоль оси x точка успевает переместиться из одного крайнего положения в другое, вдоль оси y, выйдя из нулевого положения, она успевает достигнуть одного крайнего положения, затем другого и вернуться в нулевое положение (см. рис. 1.27, à).

В случае разности фаз, равной нулю, траектория вырождается в незамкнутую кривую (см. рис. 1.27, á), по которой точка движется туда и обратно.

44

Затухающие колебания

Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать. Затухающими называются колебания, происходящие в диссипативной колебательной системе.

При небольших скоростях движения в среде сила сопротивления пропорциональна скорости:

ãäå r — коэффициент сопротивления среды. Знак минус обусловлен тем, что сила и скорость имеют противоположные направления.

Уравнение движения (второй закон Ньютона) при наличии квазиупругих сил и сил сопротивления имеет вид

max kx rvx .

ãäå — коэффициент затухания; 0 — собственная циклическая частота колебаний системы (частота, с которой происходили бы свободные колебания системы при отсутствии сопротивления среды, т. е. при r = 0), перепишем уравнение движения следующим образом:

Соотношение (1.126) называется дифференциальным уравнением затухающих колебаний.

При не слишком сильном затухании (при 0) общее решение уравнения (1.126) имеет вид

Здесь начальные амплитуда À0 и фаза определяются из начальных условий, ç — циклическая частота затухающих колебаний,

45

Логарифмический декремент затухания — натуральный логарифм от декремента затухания:

За время система успевает совершить Ne = /T колебаний. Логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за время релаксации :

Добротность Q системы — величина, пропорциональная числу колебаний, совершаемых за время релаксации :

Вынужденные колебания

Вынужденными называются такие колебания, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы (вынуждающей силы). Пусть вынуждающая сила изменяется со временем по гармоническому закону:

ãäå F0 — амплитуда вынуждающей силы; — ее частота.

При составлении уравнения движения (второго закона Ньютона) кроме вынуждающей силы необходимо учесть также и те силы, которые действуют в системе при свободных колебаниях, т. е. квазиупругую силу и силу сопротивления среды:

max kx rvx F0 cost.

С учетом обозначений (1.125) приходим к дифференциальному уравнению вынужденных колебаний:

47

Это неоднородное (правая часть отлична от нуля) дифференциальное уравнение второго порядка с постоянными коэффициентами. Как известно из теории дифференциальных уравнений, общее решение неоднородного уравнения равно сумме общего решения (1.127) однородного уравнения (1.126), соответствующего данному неоднородному, и частного решения данного неоднородного уравнения (которое можно найти по виду правой части):

Амплитуду A и отставание по фазе можно найти, непосредственно подставляя частное решение (1.139) в уравнение (1.138), откуда

Общее решение уравнения (1.138), описывающее поведение системы при вынужденных колебаниях, выглядит следующим образом:

x A0 e t cos ç t Acos t .

Первое слагаемое в этом уравнении играет заметную роль только в начальной стадии процесса при установлении колебаний. С течением времени из-за экспоненциального множителя e– t роль этого слагаемого уменьшается, и по прошествии достаточного времени им можно пренебречь, сохраняя лишь второе слагаемое.

Таким образом, функция (1.139) описывает установившиеся вынужденные колебания. Они представляют собой гармонические колебания с частотой, равной частоте вынуждающей силы. Амплитуда (1.140) вынужденных колебаний пропорциональна амплитуде вынуждающей силы. Для данной колебательной системы амплитуда зависит от частоты вынуждающей силы. Вынужденные колебания отстают по фазе от выну-

48

ждающей силы, причем величина отставания также зависит от частоты вынуждающей силы (см. (1.141)).

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к некоторому зна- чению называется резонансом, а соответствующая частота — резонанс-

ной частотой ðåç.

Выражение для резонансной частоты получаем, исследовав функцию (1.140) на максимум:

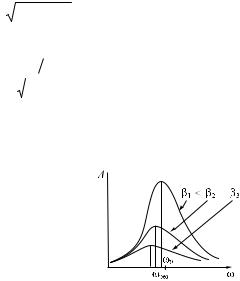
На рис. 1.29 приведены графики зависимости амплитуды при вынужденных колебаниях от частоты вынуждающей силы и от коэффициента затухания. Видно, что максимум резонансной кривой смещен влево по оси от 0; это смещение будет тем больше, чем больше коэффициент затухания .

Вредные и полезные проявления резонансных явлений наблюдаются в природе и технике. Резонанс полезен в тех случаях, когда необ-

ходимо обнаружить слабые колебания или усилить их. На этом явлении основана вся аппаратура, воспринимающая и усиливающая звуковые и электрические колебания.

Нередко явление механического резонанса служит причиной катастроф. Например, собственная частота вибра-

ций корпуса корабля или крыльев самолета должна сильно отличаться от частоты колебаний, которые могут быть возбуждены вращением гребного винта или пропеллера. В противном случае могут возникнуть разрушения. При вращении плохо отцентрированного мотора вследствие резонанса может произойти его поломка и повреждение фундамента здания, на котором расположен мотор.

49

1.4. Волновое движение

Распространение волн в упругой среде

Колебания, возбужденные в какой-либо точке среды (твердой, жидкой или газообразной), передаются от одной точки среды к другой и распространяются в ней с конечной скоростью, зависящей от свойств среды. Чем дальше расположена частица среды от источника колебаний, тем позднее она начинает колебаться. Иначе говоря, фазы колебаний частиц среды и источника тем больше отличаются друг от друга, чем больше расстояние между частицей и источником. При изучении распространения колебаний не учитывается дискретное (молекулярное) строение среды, она рассматривается как сплошная, т. е. непрерывно распределенная в пространстве и обладающая упругими свойствами.

Процесс распространения колебаний в сплошной среде называется волновым движением èëè волной. При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.

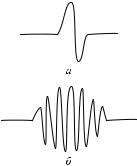
Волны могут иметь различную форму:

а) одиночной волной или импульсом называется короткое возмущение, не имеющее регулярного характера (рис. 1.30, à);

á) öóã волн — ограниченный ряд возмущений (рис. 1.30, á); в) гармоническая волна — бесконечная синусоидальная волна

(ðèñ. 1.31).

50