
Материал презентаций по физике / Лекции для заочников / Физика для гуманитариев_1 / Вотинов_Перминов_Физика
.pdf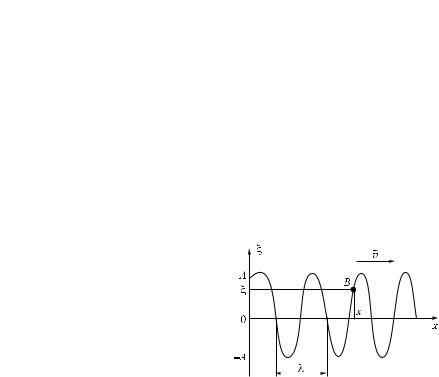
Продольные волны могут распространяться в средах, в которых воз- |
никают упругие силы при деформации сжатия и растяжения, ò. å. |
в твердых, жидких и газообразных телах. Поперечные волны могут рас- |
пространяться в среде, в которой возникают упругие силы при деформа- |
ции сдвига, т. е. фактически только в твердых телах; в жидкостях и газах |
возникают только продольные волны, а в твердых телах — как продоль- |
ные, так и поперечные. |
Упругая волна называется гармонической, если соответствующие ей |
колебания частиц являются гармоническими. На рис. 1.31 представлена |
гармоническая поперечная волна, распространяющаяся со скоростью v |
вдоль оси x, т. е. приведена зависимость между смещением частиц сре- |
ды, участвующих в волновом процессе, и расстоянием x до этих частиц |
(например, частицы Â) от источника колебаний для какого-то фиксиро- |
ванного момента времени t. |
Расстояние между ближайшими |
частицами, колеблющимися в оди- |
наковой фазе, называется длиной |
волны (см. рис. 1.31). Длина волны |
равна тому расстоянию, на которое |
распространяется волна (определен- |
ная фаза колебания) за период: |
= vT, |
(1.144) |
|
|
|
|
||
èëè |
Ðèñ. 1.31 |
||
|
|
|
|
= v, |
(1.145) |
|
|
ãäå = 1/T — частота колебаний.
Если рассмотреть волновой процесс подробнее, то ясно, что колеблются не только частицы, расположенные вдоль оси õ, но и совокупность частиц, расположенных в некотором объеме, т. е. волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства. Геометрическое место точек, до которых колебания доходят к моменту времени t, называется волновым фронтом.
Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновых поверхностей можно провести бесчисленное множество, а волновой фронт в каждый момент времени один. Волновой фронт также является волновой поверхностью. В принципе, волновые поверхности могут быть любой формы, а в про-
51

стейшем случае они представляют собой совокупность плоскостей, параллельных друг другу, или совокупность концентрических сфер. Соответственно, волна называется плоской èëè сферической.
Уравнение плоской и сферической волн. Волновое уравнение
Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат и времени:= (x, y, z, t).
Найдем вид функции в случае плоской волны, распространяющейся вдоль оси x (см. рис. 1.31). В данном случае волновые поверхности перпендикулярны оси x, а так как все точки волновой поверхности колеблются одинаково, то смещение будет зависеть только от x è t, ò. å.
= (x, t).
Рассмотрим некоторую частицу среды Â (см. рис. 1.31), находящуюся от источника колебаний на расстоянии õ. Если колебания точек, лежащих в плоскости õ = 0, описываются функцией (0, t) = A cos(t + ), то частица среды Â колеблется по тому же закону, но ее колебания будут отставать по времени от колебаний источника на , так как для прохождения волной расстояния õ требуется время = x/v, ãäå v — скорость распространения волны. Тогда уравнение колебания частиц, лежащих в плоскости õ, имеет вид
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x, t |
|
A cos t x v |
|
|
|
A cos t |
|
x , (1.146) |
|
|
|
|
|
|
|
v |
|
откуда следует, что (x, t) является не только периодической функцией времени, но и периодической функцией координаты õ.
Зафиксируем какое-либо значение фазы волны:
|
|
|
|
|
x |
|
|
t |
|
|
const. |
|
|||
|
|
||
|
v |
|
|
Взяв дифференциал этого выражения и сократив на , получим: dt dx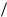 v 0, откуда
v 0, откуда
dx v. dt
52

Следовательно, скорость v распространения волны в уравнении (1.146) есть не что иное, как скорость перемещения фазы волны, поэтому ее называют фазовой скоростью.
Для характеристики волн используется также волновое число
k |
|
|
2 |
, |
(1.147) |
|
|
ñучетом которого уравнению (1.146) можно придать вид
(x, t) = A cos(t – kx + ), |
(1.148) |
ãäå (t – kx + ) — фаза распространяющейся волны, — начальная фаза, зависящая от выбора начала отсчета õ è t.
Уравнение (1.148) называют уравнением плоской волны. Если плоская волна распространяется в противоположном направлении, то
(x, t) = A cos(t + kx + ). |
(1.149) |
Если плоская волна (1.148) распространяется в среде, не поглощающей энергию, то амплитуда волны А = const.
Повторяя ход рассуждений для плоской волны, можно показать, что уравнение сферической волны, волновые поверхности которой имеют вид концентрических сфер, записывается как
(r, t) |
A0 |
cos( t kr ), |
(1.150) |
|
|||
|
r |
|
|
ãäå r — расстояние от центра волны до рассматриваемой точки среды. В случае сферической волны даже в среде, не поглощающей энергию, амплитуда колебаний не остается постоянной, а убывает с расстоянием по закону 1/r, поскольку энергия волновой поверхности распространяется по все большей площади (S = 4r2).
Если фазовая скорость волн зависит от их частоты, то это явление называется дисперсией волн, а среда, в которой наблюдается дисперсия волн,— диспергирующей средой.
Уравнение любой волны есть решение некоторого дифференциального уравнения, называемого волновым. Для плоской волны, распространяющейся вдоль оси õ, волновое уравнение имеет вид
%2 |
|
1 |
|
%2 |
|
|
|
|
|
|
. |
(1.151) |
|
%x2 |
|
|
||||
|
v 2 |
|
%t 2 |
|
||
53

Энергия упругих волн. Вектор Умова
Бегущими называются волны, которые переносят в пространстве энергию. Если поглощением энергии при распространении волны пренебречь, то можно считать, что вся энергия колебаний W частиц среды целиком определяется энергетическим излучением источника (см. соотношение (1.96)):
W mA2 2 , 2
ãäå m — масса среды, вовлеченной в колебательный процесс. Эта энергия передается частицам среды от источника и распределена в пространстве неравномерно. Средняя объемная плотность энергии, переносимой волной,
w |
W |
|
A2 2 |
, |
(1.152) |
|
|
||||
|
V |
2 |
|
|
|
где — плотность среды, в которой распространяется волна, m.
V
Итак, среда, в которой возникает волна, обладает дополнительным запасом энергии. Эта энергия доставляется от источника колебаний в различные точки среды самой волной, следовательно, волна переносит с собой энергию. Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии Ф через эту поверхность:
|
W |
. |
(1.153) |
|
|||
|
t |
|
|
Поток энергии — скалярная величина, размерность которой равна размерности энергии, деленной на размерность времени, т. е. совпадает с размерностью мощности: [Ф] = Вт.
Поток энергии в разных точках среды может обладать различной интенсивностью. Для характеристики переноса энергии в разных точках
пространства вводится векторная величина, называемая плотностью по-
тока энергии j. Этот вектор для упругих волн называется вектором
Умова. Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу
54
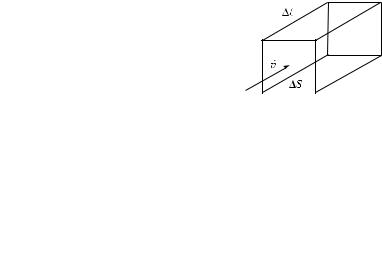
времени через единичную площадку, расположенную перпендикулярно направлению распространения волны (рис. 1.32):
j |
|
|
W |
|
w Sv t |
wv, |
|
|
|
|
|
|
|
|
|||||
|
S S t |
S t |
|
|
|||||
|
|
|
|||||||
|
|
|
|
|
|
Ðèñ. 1.32 |
|||
|
|
|
j wv. |
(1.154) |
|||||
|
|
|
|
|
|||||
Итак, вектор Умова равен произведению объемной плотности энергии на вектор скорости распространения волны.
Интенсивность волны J — среднее значение энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны:
J w v |
1 |
v 2 A2 . |
(1.155) |
|
|||
2 |
|
|
|
Интерференция волн
При одновременном распространении нескольких волн колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности, т. е. волны просто накладываются одна на другую, не возмущая друг друга. Это утверждение называется принципом суперпозиции (наложения) волн.
Âслучае, когда колебания, обусловленные отдельными волнами
âкаждой из точек среды, обладают постоянной разностью фаз, волны называют когерентными. Очевидно, что когерентными могут быть лишь волны, имеющие одинаковую частоту. В более широком смысле под когерентностью понимают согласованное протекание двух и более колебательных или волновых процессов.
При наложении двух (или более) когерентных волн в разных точках пространства получается усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн. Это явление называется интерференцией волн.
Рассмотрим две волны, распространяющиеся от точечных источников O1 è O2, колеблющихся с постоянной разностью фаз (такие источники называют, как и порождаемые ими волны, когерентными). Опреде-
55

лим результирующее колебание в какой-либо точке среды при условии, что оба колебания, вызываемые каждой из волн в отдельности, имеют одинаковое направление.
Пусть фазы колебаний источников O1 è O2 равны соответственно (t + 1) è (t + 2). Тогда колебание в данной точке будет равно сумме колебаний:
1(x, t) = A1 cos(t – kr1 + 1),
2(x, t) = A2 cos(t – kr2 + 2),
ãäå A1 è A2 — амплитуды волн в рассматриваемой точке; k — волновое число; r1 è r2 — расстояния от источников волн до рассматриваемой точки.
В точках, определяемых условием
k r1 r2 1 2 2m, m = 0, 1, 2, …, |
(1.156) |
колебания усиливают друг друга и результирующее движение представляет собой гармоническое колебание частоты с амплитудой (A1 + A2).
Условие (1.156) называется условием интерференционного максимума.
В точках, для которых
1 |
2 |
|
|
|
2 |
|
1 |
|
1 |
|
|
|
|
||||
k r |
r |
|
|
|
|
2 n |
2 |
, n = 0, 1, 2, …, (1.157) |
|
|
|
|
|
|
|
|
колебания ослабляют друг друга и результирующее движение является гармоническим колебанием с амплитудой |A1 – A2|. В частном случае, когда A1 = A2, колебания в этих точках будут отсутствовать.
Стоячие волны
Особым случаем интерференции являются стоячие волны — это колебательный процесс, наблюдающийся при наложении двух встречных волн с одинаковыми амплитудами и частотами.
Рассмотрим две плоские волны, распространяющиеся навстречу друг другу вдоль оси õ в среде без затухания, причем обе волны характеризуются одинаковыми частотами и амплитудами (см. соотношения (1.148) и (1.149)). Кроме того, начало координаты x и отсчет времени t выберем для простоты таким образом, чтобы 1 = 2 = 0. Тогда соответственно уравнения волны, распространяющейся вдоль положительного
56

направления оси õ, и волны, распространяющейся ей навстречу, будут иметь вид:
1(x, t) = A cos( t – kx),
2(x, t) = A cos( t + kx).
Сложив эти уравнения, преобразовав результат по формуле для суммы косинусов и учтя, что k = 2 / , получим уравнение стоячей волны:
= 1 + 2 = 2Acos kx cos t = 2Acos(2x/)cos t. |
(1.158) |
Из этого уравнения следует, что в каждой точке стоячей волны происходят колебания одной и той же частоты с амплитудой
Àñò = |2Àcos (2 x/ )|,
зависящей от координаты õ рассматриваемой точки. В точках среды, где
2x/ m, m 0, 1, 2, …,
амплитуда колебаний достигает максимального значения, равного 2À. Эти точки называются пучностями стоячей волны. Из этого условия получаются значения координат пучностей:
xïó÷í m |
|
, |
m = 0, 1, 2, …. |
(1.159) |
|
||||
2 |
|
|
|
|
В точках среды, где |
|
|
|
|
2x/ = (m + 1/2), |
m = 0, 1, 2, …, |
|
||
амплитуда колебаний обращается в нуль. Эти точки называются узлами стоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают. Координаты узлов:
|
|
|
|
|
|
|
1 |
|
|
|
|
xóçë m |
|
|
, m = 0, 1, 2, …. |
(1.160) |
|
|
|
||||
|
|
2 |
|||
|
2 |
|
|
||
Из формул (1.159) и (1.160) следует, что расстояния между двумя соседними пучностями и двумя соседними узлами одинаковы и равны /2. Расстояние между соседними пучностью и узлом стоячей волны равно /4.
В отличие от бегущей волны, все точки которой совершают колебания с одинаковой амплитудой, но с запаздыванием по фазе, все точки
57

|
|
|
|
|
|
|
|
|
|
|
|
стоячей волны между двумя узлами колеблют- |
||
|
|
|
|
|
|
|
|
|
|
|
|
ся с разными амплитудами, с одинаковыми фа- |
||
|
|
|
|
|
|
|
|
|
|
|
|
зами. При переходе |
через узел |
множитель |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2A cos(2x/ ) в уравнении (1.158) меняет свой |
||
|
|
|
|
|
|
|
|
|
|
|
|
знак, поэтому фаза колебаний по разные сторо- |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
ны от узла отличается на , т. е. точки, лежа- |
||
|
|
|
|
|
|
|
|
|
|
|
|
щие по разные стороны от узла, колеблются |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
в противофазе. Образование стоячих волн на- |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
блюдается при интерференции бегущей и отра- |
||
|
|
|
|
|
|
|
|
|
|
|
|
женной волн. Что будет на границе отраже- |
||
|
|
|
|
|
|
|
|
|
|
|
|
ния — узел или пучность, зависит от соотноше- |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
ния плотностей сред. Если среда, от которой |
||
|
Ðèñ. 1.33 |
|
|
|
||||||||||
|
|
|
|
происходит отражение, менее плотная, то в |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
месте отражения |
получается |
пучность |
(ðèñ. 1.33, à), если более плотная — узел (рис. 1.33, á). В случае стоячей волны переноса энергии не наблюдается.
1.5. Основы гидроаэромеханики
Гидроаэромеханика — раздел механики, изучающий равновесие и движение жидкостей и газов, их взаимодействие между собой и обтекаемыми ими твердыми телами. В данном разделе используется единый подход к изучению жидкостей и газов.
Хотя свойства жидкостей и газов во многом отличаются, в ряде механических явлений их поведение определяется одинаковыми параметрами и идентичными уравнениями.
В механике жидкости и газы рассматриваются как сплошные, непрерывно распределенные в занятой ими части пространства.
Отличительной особенностью жидкостей и газов является их теку- честь, которая связана с малыми силами трения при относительном движении соприкасающихся слоев. При бесконечном уменьшении скорости относительного движения слоев силы трения между ними стремятся к нулю. Этим объясняется отсутствие сил трения покоя в жидкостях и газах.
Статика жидкостей и газов
Если в покоящуюся жидкость поместить тонкую пластинку, то части жидкости, находящиеся по разные стороны от нее, будут действовать на каждый ее элемент S с силами F. Эти силы независимо от того, как
58

пластинка ориентирована, будут равны по модулю и направлены перпендикулярно S, так как наличие касательных сил привело бы частицы жидкости в движение.
Физическая величина, определяемая нормальной силой, действующей со стороны жидкости или газа на единицу площади, называется давлением жидкости ð:
p lim |
F |
|
dF |
. |
(1.161) |
|
|
||||
S 0 S dS |
|
||||
Единица измерения давления — паскаль (Ïà). 1 Ïà = 1 Í/ì2. Давление может также измеряться в атмосферах (àòì), миллиметрах ртутного столба (мм. рт. ст.) и других единицах. Полезно знать связь между ними:
1 àòì = 760 ìì. ðò. ñò. = 1,013·105 Ïà.
Давление при равновесии жидкостей (газов) подчиняется закону Паскаля: давление в любом месте покоящейся жидкости или газа одинаково передается по всем направлениям, иначе говоря, силы, действующие со стороны жидкости (газа) на маленькую пластинку (площадку), не зависят от ее ориентации в данной точке пространства.
Давление в жидкостях, находящихся в силовых полях (например, в поле силы тяжести), увеличивается с глубиной. Давление, обусловленное весом верхних слоев жидкости, называется гидростатическим. При равновесии жидкости давление по горизонтали всегда одинаково, иначе не было бы равновесия. Поэтому свободная поверхность жидкости в состоянии покоя всегда горизонтальна вдали от стенок сосуда. Если жидкость несжимаема, то ее плотность не зависит от давления. Тогда при поперечном сечении S столба жидкости, его высоте h и плотности вес жидкости Ð = gSh, а давление жидкости на нижнее основание
pæèäê |
P |
|
gSh |
gh, |
(1.162) |
|
|
||||
|
S S |
|
|||
т. е. давление жидкости изменяется линейно с глубиной.
Полное давление в покоящейся жидкости складывается из атмосферного и гидростатического:
p = p0 + gh. |
(1.163) |
Силы давления на нижние части поверхности погруженного в жидкость (газ) тела будут больше, чем на верхние, поэтому на тело действует
59
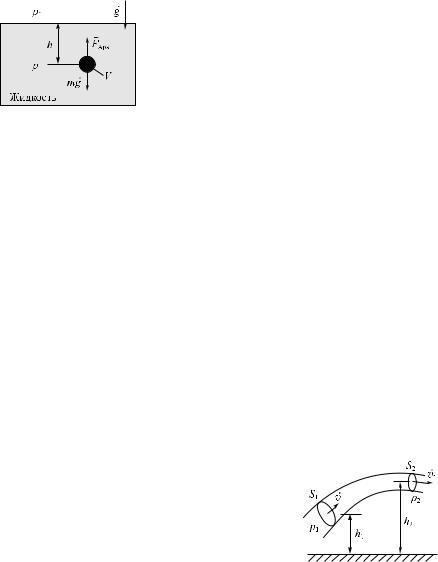
выталкивающая сила, определяемая законом Архимеда: на тело, погруженное в жидкость (газ), действует со стороны этой жидкости (газа) направленная вверх выталкивающая сила, равная весу вытесненной телом жидкости (газа):
Ðèñ. 1.34 FAðõ = gV, (1.164)
где — плотность жидкости; V — объем вытесненной телом жидкости (рис. 1.34).
Уравнения неразрывности и Бернулли
Воображаемая жидкость, в которой отсутствуют силы внутреннего трения, называется идеальной.
Линиями тока называются такие линии, касательные к которым совпадают с векторами скорости жидкости в соответствующих точках пространства.
Поскольку величина и направление вектора скорости могут изменяться со временем, то и картина линий тока также может изменяться. Если вектор скорости в каждой точке пространства остается постоянным, то течение называется установившимся èëè стационарным. Линии тока при стационарном течении совпадают с траекториями частиц.
Часть жидкости, ограниченная линиями тока, называется трубкой тока (рис. 1.35). Жидкость при своем движении не пересекает стенок трубки тока, так как вектор скорости в каждой точке направлен (по определению) по касательной к линиям тока, из которых состоит трубка тока.
Возьмем трубку тока настолько тонкую, что для произвольного сечения скорость можно счи- тать одинаковой в каждой точке этого сечения. За время t через сечение S трубки тока протека-
ет жидкость объемом, равным Sv t. Åñëè æèä-
кость несжимаема (т. е. плотность всюду одинакова и изменяться не может), то количество жид-
кости между произвольными сечениями S1 è S2 трубки тока (см. рис. 1.35) будет оставаться неиз-
менным. Отсюда следует, что объемы жидкости, протекающей за единицу времени через произвольные сечения S1 è S2, одинаковы: S1v1 = S2v2.
60
