Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

Файл:

General Physics part 1 / PhysPraktikum / Woan G. The Cambridge Handbook of Physics Formulas (CUP, 2000)(ISBN 0521573491)(230s)_PRef_.pdf

Скачиваний:

Добавлен:

27.03.2015

Размер:

1.65 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 359 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

44	Mathematics

2.8 Integration

Standard formsa

u dv = [uv] −

v du

(2.353)

xn dx =

xn+1

(n = −1)

(2.355)

n+ 1

eax dx =

eax

(2.357)

lnax dx = x(lnax− 1)

(2.359)

xlnax dx =

lnax−

(2.361)

dx =

ln(a+ bx)

(2.363)

a+ bx

dx =

−1

(2.365)

(a+ bx)2

b(a+ bx)

x(xn + a)

dx =

+ a

(2.367)

dx =

ln|x2 ± a2|

(2.369)

x2 ± a2

dx = arcsin

(2.371)

(a2 − x2)1/2

dx = (x2 ± a2)1/2

(2.373)

(x2 ± a2)1/2

uv dx = v u dx− u dx dx dx

(2.354)

dx = ln|x|

(2.356)

xeax dx = eax

−

(2.358)

f((x)) dx = lnf(x)

(2.360)

bax dx =

(b > 0)

(2.362)

alnb

a+ bx

= −

(2.364)

x(a+ bx)

arctan

(2.366)

a2 + b2x2

−

x− a

dx =

(2.368)

x+ a

dx =

−1

(2.370)

(x2 ± a2)n

2(n−

1)(x2 ± a2)n−1

dx = ln|x+ (x2 ± a2)1/2|

(2.372)

(x2

a2)1/2

−

dx =

arcsec

(2.374)

x(x2

a2)1/2

aa and b are non-zero constants.

2.8 Integration	45

Trigonometric and hyperbolic integrals

sinx dx = − cosx

(2.375)

sinhx dx = coshx

(2.376)

cosx dx = sinx

(2.377)

coshx dx = sinhx

(2.378)

tanx dx = − ln| cosx|

(2.379)

tanhx dx = ln(coshx)

(2.380)

tanh

cscx dx = ln

tan

(2.381)

cschx dx = ln

(2.382)

(2.383)

(2.384)

secx dx = ln| secx+ tanx|

sechx dx = 2arctan(e

)

cotx dx = ln| sinx|

(2.385)

cothx dx = ln| sinhx|

(2.386)

sinmx· sinnx dx =

sin(m n)x

sin(m+ n)x

2(m −n)

−

(m2 =n2)

(2.387)

2(m+ n)

sinmx· cosnx dx = −

−

cos(m+ n)x

cos(m n)x

2(m −n)

−

(m2 =n2)

(2.388)

2(m+ n)

cosmx· cosnx dx =

−

sin(m n)x

sin(m+ n)x

2(m −n)

(m2 =n2)

(2.389)

2(m+ n)

−

Named integrals

Error function

erf(x) =

exp(−t2) dt

(2.390)

π1/2

function

erfc(x) = 1 − erf(x) = π1/2

x∞ exp(−t2) dt

(2.391)

Complementary error

πt2

C(x) = 0

cos

dt;

S(x) = 0

sin

(2.392)

Fresnel integralsa

+ i

π1/2

C(x) + i S(x) =

erf

(1 − i)x

(2.393)

Exponential integral

Ei(x) = −∞

dt (x > 0)

(2.394)

Gamma function

Γ(x) = 0

∞ tx−1e−t dt

(x > 0)

(2.395)

F(φ,k) = 0

dθ

(ﬁrst kind)

(2.396)

Elliptic integrals

(1 − k2 sin2 θ)1/2

(trigonometric form)

E(φ,k) = 0

(1 − k2 sin2 θ)1/2 dθ

(second kind)

(2.397)

aSee also page 167.

46	Mathematics

Deﬁnite integrals

∞ e−ax

dx =

2 a !

(a > 0)

1/2

∞ xe−ax

dx = 2a (a > 0)

∞ xne−ax dx = an+1

(a > 0; n = 0,1,2,...)

−∞

exp a

(a > 0)

∞ exp(2bx− ax2) dx =

1/2

∞

e−

ax2

...

1)(2a)−(n+1)/2(π/2)1/2

dx = "2

· 4

· 6

· ...

· (n

− 1)(2a)−(n+1)/2

−

p!q!

xp(1 − x)q dx =

(p,q integers > 0)

(p+ q + 1)!

∞ cos(ax2) dx = 0

∞ sin(ax2) dx = 2

2a!

(a > 0)

1/2

0 ∞

sinx

dx =

0 ∞

sin2 x

dx =

∞ (1 +1x)xa dx = sinaπ

(0 < a < 1)

(2.398)

(2.399)

(2.400)

(2.401)

n > 0 and even

(2.402)

n > 1 and odd

(2.403)

(2.404)

(2.405)

(2.406)

2.9Special functions and polynomials

Gamma function

Deﬁnition

Γ(z) = 0

∞ tz−1e−t dt

[ (z) > 0]

(2.407)

n! = Γ(n+ 1) = nΓ(n)

(n = 0,1,2,...)

(2.408)

Relations

Γ(1/2) = π1/2

(2.409)

Γ(z + 1)

w =

(2.410)

w!(z w)!

Γ(w + 1)Γ(z

−

w + 1)

−

− · · ·

Γ(z) e−zzz−(1/2)(2π)1/2

1 +

(2.411)

Stirling’s formulas

12z

288z2

(for |z|,n 1)

n! nn+(1/2) e−n(2π)1/2

(2.412)

ln(n!) nlnn− n

(2.413)

2.9 Special functions and polynomials	47

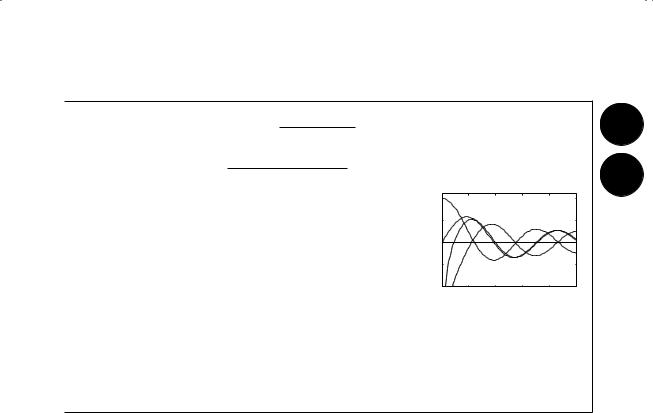
Bessel functions

Jν (x) =

∞

(−x2/4)k

(2.414)

Series

k=0 k!Γ(ν + k + 1)

expansion

Yν (x) =

Jν (x)cos(πν) − J−ν (x)

(2.415)

sin(πν)

Approximations

x ν)

Jν (x)

Γ(ν+1)

1 νπ

(2.416)

1/2 cos x

≤

ν)

−Γ(ν)

−ν

−

(0 < x ν)

πx

Yν (x)

−

(2.417)

1/2

sin x

1 νπ

ν)

πx

Modiﬁed Bessel

Iν (x) = (−i)ν Jν (ix)

(2.418)

functions

Kν (x) =

ν+1

[Jν

(ix) + iYν (ix)]

(2.419)

2 i

Spherical Bessel

1/2

function

jν (x) =

Jν+ 21 (x)

(2.420)

Jν (x)	Bessel function of the ﬁrst
	kind
Yν (x)	Bessel function of the	2
	second kind	2
	second kind
Γ(ν)	Gamma function
ν	order (ν ≥ 0)

1 J0

0.5 J1

−0.5

−1

0 2 4 x 6 8 10

Iν (x) modiﬁed Bessel function of the ﬁrst kind

Kν (x) modiﬁed Bessel function of the second kind

jν (x) spherical Bessel function of the ﬁrst kind [similarly for yν (x)]

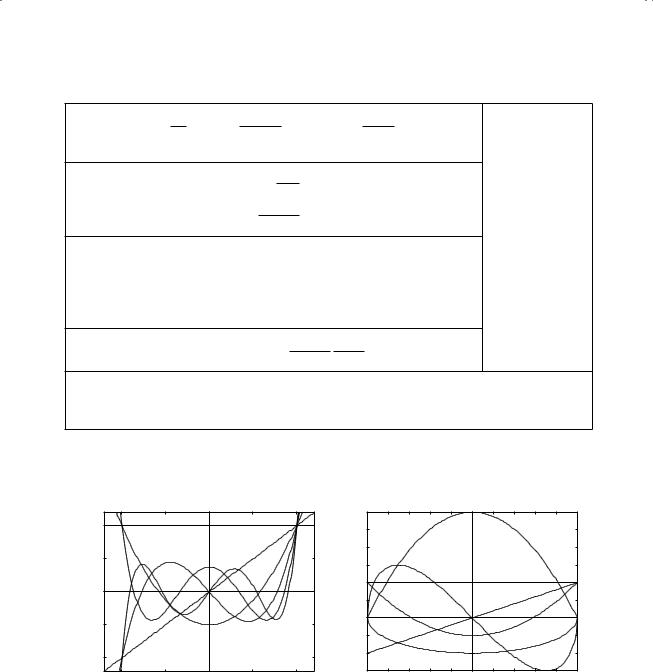
Legendre polynomialsa

Legendre

d2Pl(x)

dPl(x)

Legendre

equation

− x

)

dx2

− 2x

+ l(l + 1)Pl(x) = 0

polynomials

(2.421)

order (l ≥ 0)

Rodrigues’

Pl(x) =

(x2 − 1)l

(2.422)

formula

2ll!

dxl

Recurrence

(l + 1)Pl+1(x) = (2l + 1)xPl(x) − lPl−1(x)

(2.423)

relation

Orthogonality

−1 Pl(x)Pl (x) dx =

δll

(2.424)

δll

Kronecker delta

2l + 1

Explicit form

(x) = 2−l m=0(−1)m ml 2l −l

2m xl−2m

(2.425)

binomial coe cients

l/2

wavenumber

Expansion of

exp(ikz) = exp(ikrcosθ)

(2.426)

propagation axis

∞

z = rcosθ

plane wave

jl(kr)Pl(cosθ)

(2.427)

spherical Bessel

(2l + 1)i

l=0

function of the ﬁrst

kind (order l)

P0(x) = 1

P2(x) = (3x2 − 1)/2

P4(x) = (35x4 − 30x2 + 3)/8

P1(x) = x

P3(x) = (5x3 − 3x)/2

P5(x) = (63x5 − 70x3 + 15x)/8

aOf the ﬁrst kind.

48	Mathematics

Associated Legendre functionsa

Associated

(1 − x2)

dP m(x)

Plm(x) = 0

P m

associated

Legendre

dl x

+ l(l + 1) − 1

−

Legendre

equation

(2.428)

functions

From

2 m/2

(x) = (1 − x )

dxm Pl(x),

0 ≤ m ≤ l

(2.429)

Legendre

1)m (l − m)! Plm(x)

polynomials

Pl−m(x) = (

−

(2.430)

(l + m)!

P m

(x) = x(2m+ 1)P m(x)

(2.431)

m+1

Recurrence

(x) = (−1)

m/2

5!! = 5· 3· 1 etc.

relations

(2m− 1)!!(1 − x

)

(2.432)

(l − m+ 1)Plm+1(x) = (2l + 1)xPlm(x) − (l + m)Plm−1(x)

(2.433)

(l + m)!

δll

Kronecker

Orthogonality

−1 Plm(x)Plm(x) dx = (l − m)! 2l + 1 δll

(2.434)

delta

P00(x) = 1

P10(x) = x

P11(x) = −(1 − x2)1/2

P20(x) = (3x2 − 1)/2

P21(x) = −3x(1 − x2)1/2

P22(x) = 3(1 − x2)

aOf the ﬁrst kind. Plm(x) can be deﬁned with a (−1)m factor in Equation (2.429) as well as Equation (2.430).

Legendre polynomials

associated Legendre functions

0.5

P 0

−

0.5

−1

−1 −0.5

0.5

−1

2.9 Special functions and polynomials	49

Spherical harmonics

Di erential

∂

∂2

Y m

spherical

equation

sinθ ∂θ sinθ ∂θ

+ sin2 θ ∂φ2

+ l(l + 1)Yl

= 0

harmonics

(2.435)

2l + 1 (l − m)!

1/2

Ylm(θ,φ) = (

1)m

Plm(cosθ)eimφ

Legendre

−

P m

associated

Deﬁnition

4π

(l + m)!

(2.436)

functions

complex

2π

conjugate

Orthogonality

Y m (θ,φ)Y m

(θ,φ)sinθ dθ dφ = δmm

δll

(2.437)

Kronecker

φ=0 θ=0

delta

∞

Y m(θ,φ)

f(θ,φ) =

(2.438)

Laplace series

l=0 m=−l

continuous

2π

where

alm = φ=0

θ=0 Ylm (θ,φ)f(θ,φ)sinθ dθ dφ

(2.439)

function

Solution to

2ψ(r,θ,φ) = 0,

then

continuous

Laplace

∞

function

Ylm(θ,φ) ·

equation

ψ(r,θ,φ) =

almrl + blmr−(l+1)

(2.440)

a,b

constants

l=0 m=−l

Y00

(θ,φ) =

Y10

(θ,φ) =

cosθ

4π

Y1±1(θ,φ) =

sinθe±iφ

(θ,φ) =

Y20

cos2 θ −

8π

4π

Y2±1(θ,φ) =

sinθcosθe±iφ

Y2±2

(θ,φ) =

sin2 θe±2iφ

8π

32π

Y30

(θ,φ) =

(5cos2 θ − 3)cosθ

Y3±1

(θ,φ) =

sinθ(5cos2 θ − 1)e±iφ

4π

Y3±2

(θ,φ) =

105

sin2 θcosθe±2iφ

Y3±3

(θ,φ) =

sin3 θe±3iφ

2π

4π

aDeﬁned for −l ≤ m ≤ l, using the sign convention of the Condon–Shortley phase. Other sign conventions are possible.

50 Mathematics

Delta functions

if i = j

Kronecker delta

δij = "0

if i = j

(2.441)

δij

Kronecker delta

δii = 3

(2.442)

i,j,k,... indices (= 1,2 or 3)

123 = 231 = 312 = 1

Three-

132 = 213 = 321 = −1

(2.443)

dimensional

all other ijk = 0

Levi–Civita

ijk klm = δilδjm − δimδjl

(2.444)

ijk

Levi–Civita symbol

symbol

(see also page 25)

(permutation

δij ijk = 0

(2.445)

tensor)a

ilm jlm = 2δij

(2.446)

ijk ijk = 6

(2.447)

b δ(x) dx = "1

if a < 0 < b

(2.448)

otherwise

Dirac delta

f(x)δ(x− x0) dx = f(x0)

(2.449)

δ(x)

Dirac delta function

function

δ(x− x0)f(x) = δ(x− x0)f(x0)

(2.450)

f(x) smooth function of x

a,b

constants

δ(−x) = δ(x)

(2.451)

δ(ax) = a −1δ(x)

(a = 0)

(2.452)

δ(x)

| |

(2.453)

nπ−1/2e−n x

aThe general symbol ijk... is deﬁned to be +1 for even permutations of the su ces, −1 for odd permutations, and 0 if a su x is repeated. The sequence (1,2,3,... ,n) is taken to be even. Swapping adjacent su ces an odd (or even)

number of times gives an odd (or even) permutation.

2.10 Roots of quadratic and cubic equations Quadratic equations

Equation	ax	2	+ bx+ c = 0				(a = 0)	(2.454)	x	variable
Equation	ax		+ bx+ c = 0				(a = 0)	(2.454)	a,b,c	real constants

				−b± √
	x1,2		=	−b± √		b2 − 4ac		(2.455)
Solutions					2a				x1,x2	quadratic roots
Solutions				−2c					x1,x2	quadratic roots
			=	−2c				(2.456)

				b± √b2 − 4ac
				b± √b2 − 4ac
Solution	x1 + x2 = −b/a							(2.457)
combinations	x1x2 = c/a							(2.458)

2.10 Roots of quadratic and cubic equations	51

Cubic equations

(a = 0)

variable

Equation

+ bx

+ cx+ d = 0

(2.459)

a,b,c,d

real constants

p =

−

(2.460)

Intermediate

2b3

9bc

27d

deﬁnitions

q =

−

(2.461)

discriminant

D =

(2.462)

If D ≥ 0, also deﬁne:

If D < 0, also deﬁne:

!1/3

u =

−q

+ D1/2

1/3

(2.463)

φ = arccos

−q

|p|

−3/2

(2.467)

v =

−q

−

D1/2

(2.464)

|p|

1/2

= 2

cos

(2.468)

(2.465)

y1 = u+ v

y2,3 =

−(u+ v)

u− v

31/2

(2.466)

y2,3

−

|p|

1/2 cos

φ± π

(2.469)

1 real, 2 complex roots

(if D = 0: 3 real roots, at least 2 equal)

3 distinct real roots

Solutionsa

cubic roots

xn = yn − 3a

(2.470)

(n = 1,2,3)

Solution

x1 + x2 + x3 = −b/a

(2.471)

combinations

x1x2 + x1x3 + x2x3 = c/a

(2.472)

x1x2x3 = −d/a

(2.473)

ayn are solutions to the reduced equation y3 + py + q = 0.

52 Mathematics

2.11 Fourier series and transforms Fourier series

∞

nπx

f(x) =

+ n=1

an cos

+ bn sin

(2.474)

f(x)

periodic

function,

nπx

period 2L

Real form

−L f(x)cos

an =

(2.475)

an,bn

Fourier

nπx

coe cients

−L f(x)sin

bn =

(2.476)

nπx

∞

cn exp

(2.477)

Complex

f(x) = n=

complex

form

−∞

Fourier

inπx

coe cient

cn =

−L f(x)exp

−

(2.478)

∞

L |f(x)|2 dx =

an2 + bn2

(2.479)

Parseval’s

−

2 n=1

modulus

theorem

∞

|cn|2

(2.480)

n=−∞

Fourier transforma

			∞
Deﬁnition 1	F(s) = −∞ f(x)e−2πixs dx					(2.481)	f(x) function of x
			∞				F(s) Fourier transform of f(x)
	f(x) = −∞ F(s)e2πixs ds					(2.482)
			∞
Deﬁnition 2	F(s) = −∞ f(x)e−ixs dx					(2.483)
	1				∞
	f(x) =			−∞ F(s)eixs ds		(2.484)
		2π
	1				∞
	F(s) =	√			−∞ f(x)e−ixs dx	(2.485)
Deﬁnition 3			2π
	1				∞
	f(x) =	√			−∞ F(s)eixs ds	(2.486)
			2π

aAll three (and more) deﬁnitions are used, but deﬁnition 1 is probably the best.

2.11 Fourier series and transforms	53

Fourier transform theoremsa

	∞		f,g	general functions
Convolution	f(x) g(x) = −∞ f(u)g(x− u) du	(2.487)		convolution

Convolution

f g = g f

(2.488)

f(x) F(s)

rules

f (g h) = (f g) h

(2.489)

g(x) G(s)

Convolution

Fourier transform

theorem

f(x)g(x) F(s) G(s)

(2.490)

relation

Autocorrela-

∞

correlation

(x) f(x) =

−

x)f(u) du

(2.491)

complex

tion

−∞

conjugate of f

Wiener–

f (x)

f(x) |F(s)|2

Khintchine

(2.492)

theorem

Cross-

∞

correlation

f (x)

g(x) =

−∞ f (u− x)g(u) du

(2.493)

h,j

real functions

Correlation

h(x) j(x) H(s)J (s)

(2.494)

H(s) h(x)

theorem

(x)

J(s) j

Parseval’s

∞

relationb

−∞ f(x)g (x) dx = −∞ F(s)G (s) ds

(2.495)

Parseval’s

∞

theoremc

−∞ |f(x)|2 dx = −∞ |F(s)|2 ds

(2.496)

df(x)

Derivatives

2πisF(s)

(2.497)

df(x)

dg(x)

[f(x) g(x)] =

g(x) =

f(x)

(2.498)

aDeﬁning the Fourier transform as F(s) = ∞ f(x)e−2πixs dx.

%−∞

c Also called the “power theorem.”

Also called “Rayleigh’s theorem.”

Fourier symmetry relationships

f(x)

F(s)

deﬁnitions

even

real: f(x) = f (x)

odd

imaginary: f(x) =

−

f (x)

real, even

even: f(x) = f(−x)

real, odd

imaginary, odd

odd: f(x) = −f(−x)

imaginary, even

Hermitian: f(x) = f (−x)

complex, even

anti-Hermitian: f(x) =

−

f (

−

complex, odd

real, asymmetric

complex, Hermitian

imaginary, asymmetric

complex, anti-Hermitian

54	Mathematics

Fourier transform pairsa

										f(x)
										f(x)
									f(ax)
									f(ax)
									f(x− a)
									f(x− a)
									dn
									dxn f(x)
										δ(x)
										δ(x)
									δ(x− a)
									δ(x− a)
									e−a\|x\|
									xe−a\|x\|
									e−x2/a2
									sinax
									sinax
									cosax
									cosax
							∞
								δ(x− ma)
						m=−∞		δ(x− ma)
						m=−∞
					0	x < 0
		f(x) = "1				x > 0			(“step”)
	f(x) =			1	x ≤ a		(“top hat”)
		"0			\|x\|	> a
	1				\| \|
			x
f(x) =		−	\|a\|		\|x\| ≤ a		(“triangle”)
					\| \|	> a
	0				x	> a

∞

F(s) = −∞ f(x)e−2πisx dx

(2.499)

F(s/a)

(a = 0, real)

(2.500)

|a|

e−2πiasF(s)

(a real)

(2.501)

(2πis)nF(s)

(2.502)

(2.503)

e−2πias

(2.504)

(a > 0)

(2.505)

a2 + 4π2s2

8iπas

(a > 0)

(2.506)

(a2 + 4π2s2)2

a√

e−π2a2s2

(2.507)

!− δ

s+ 2π !

2i δ

s− 2π

(2.508)

s−

2π !+ δ

s+ 2π !

(2.509)

∞

s−

(2.510)

n=−∞ δ

δ(s) −

(2.511)

2πs

sin2πas

= 2asinc2as

(2.512)

πs

(1 − cos2πas) = asinc2 as

(2.513)

2π2as2

aEquation (2.499) deﬁnes the Fourier transform used for these pairs. Note that sincx ≡ (sinπx)/(πx).

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 359 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>