Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

Файл:

General Physics part 1 / PhysPraktikum / Woan G. The Cambridge Handbook of Physics Formulas (CUP, 2000)(ISBN 0521573491)(230s)_PRef_.pdf

Скачиваний:

Добавлен:

27.03.2015

Размер:

1.65 Mб

Скачать

☆

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 1415 / 3515 16 17 18 19 20 21 22 23 24 25 26 27 > Следующая >>>

Chapter 4 Quantum physics

	4.1 Introduction
	Quantum ideas occupy such a pivotal position in physics that di erent notations and algebras
		4
	appropriate to each ﬁeld have been developed. In the spirit of this book, only those formulas	4

	that are commonly present in undergraduate courses and that can be simply presented in
	tabular form are included here. For example, much of the detail of atomic spectroscopy and of
	speciﬁc perturbation analyses has been omitted, as have ideas from the somewhat specialised

	ﬁeld of quantum electrodynamics. Traditionally, quantum physics is understood through
	standard “toy” problems, such as the potential step and the one-dimensional harmonic
	oscillator, and these are reproduced here. Operators are distinguished from observables using
	the “hat” notation, so that the momentum observable, px, has the operator pˆx = −i¯h∂/∂x.
	For clarity, many relations that can be generalised to three dimensions in an obvious way
	have been stated in their one-dimensional form, and wavefunctions are implicitly taken as
	normalised functions of space and time unless otherwise stated. With the exception of the
	last panel, all equations should be taken as nonrelativistic, so that “total energy” is the sum
	of potential and kinetic energies, excluding the rest mass energy.

90	Quantum physics

4.2Quantum deﬁnitions

Quantum uncertainty relations

p =

(4.1)

p,p

particle momentum

De Broglie relation

Planck constant

¯h

h/(2π)

p = ¯hk

(4.2)

de Broglie wavelength

de Broglie wavevector

Planck–Einstein

E = hν = ¯hω

(4.3)

energy

relation

frequency

angular frequency (= 2πν)

observablesb

(∆a)

= (a

− a )

(4.4)

a,b

Dispersiona

expectation value

−

a 2

(4.5)

dispersion of a

(∆a)2

General uncertainty

≥

i[a,ˆ

aˆ

operator for observable a

relation

(∆a)

(∆b)

(4.6)

[·,·]

commutator (see page 26)

Momentum–position

¯h

particle position

uncertainty relationc

∆p∆x ≥ 2

(4.7)

Energy–time

¯h

time

uncertainty relation

∆E ∆t ≥ 2

(4.8)

Number–phase

∆n∆φ ≥

(4.9)

number of photons

uncertainty relation

wave phase

aDispersion in quantum physics corresponds to variance in statistics. bAn observable is a directly measurable parameter of a system.

cAlso known as the “Heisenberg uncertainty relation.”

Wavefunctions

Probability

pr(x,t) dx = |ψ(x,t)|

(4.10)

probability density

density

wavefunction

¯h

∂ψ

j ,j probability density current

j(x) =

(4.11)

¯h

(Planck constant)/(2π)

∂x

−

Probability

¯h

2im

∂x

position coordinate

density

j =

ψ (r) ψ(r)

ψ(r)

ψ (r)

(4.12)

pˆ

momentum operator

current

2im

−

particle mass

(ψ pˆ ψ)

(4.13)

real part of

time

Continuity

· j =

−

∂

(ψψ )

(4.14)

equation

∂t

Schrodinger¨

∂ψ

(4.15)

equation

Hψ = i¯h

∂t

Hamiltonian

Particle

¯h2 ∂2ψ(x)

potential energy

stationary

− 2m

∂x2

+ V (x)ψ(x) = Eψ(x)

(4.16)

total energy

statesb

aFor particles. In three dimensions, suitable units would be particles m−2 s−1. bTime-independent Schrodinger¨ equation for a particle, in one dimension.

4.2 Quantum deﬁnitions	91

Operators

Hermitian

(aφˆ ) ψ dx = φ aψˆ dx

aˆ

Hermitian conjugate

conjugate

(4.17)

operator

ψ,φ

normalisable functions

Position

xˆn = xn

(4.18)

complex conjugate

operator

x,y

position coordinates

Momentum

pˆn

¯hn

∂n

(4.19)

arbitrary integer ≥ 1

operator

∂xn

momentum coordinate

Kinetic energy

¯h2 ∂2

kinetic energy

−

(4.20)

¯h

(Planck constant)/(2π)

operator

2m ∂x2

particle mass

Hamiltonian

¯h2 ∂2

Hamiltonian

−

operator

+ V (x)

(4.21)

potential energy

∂x2

Angular

angular momentum along

momentum

Lz = xpˆ ˆy − ypˆ ˆx

ˆ 2

(4.22)

z axis (sim. x and y)

ˆ2

ˆ 2

operators

= Lx

+ Ly

+ Lz

(4.23)

total angular momentum

parity operator

Parity operator

P ψ(r) = ψ(−r)

(4.24)

position vector

Expectation value

Expectation

a =

aˆ = Ψ aˆ

Ψ dx

(4.25)

expectation value of a

aˆ

operator for a

valuea

(spatial) wavefunction

= Ψ|aˆ|Ψ

(4.26)

(spatial) coordinate

Time

∂aˆ

time

dependence

aˆ

[H,aˆ ˆ] +

(4.27)

¯h

(Planck constant)/(2π)

¯h

∂t

aψˆ

n = anψn and

Ψ =

cnψn

ψn

eigenfunctions of aˆ

Relation to

eigenvalues

eigenfunctions

dummy index

then

a = |cn|

(4.28)

probability amplitudes

particle mass

Ehrenfest’s

= p

(4.29)

position vector

theorem

= − V

(4.30)

momentum

potential energy

aEquation (4.26) uses the Dirac “bra-ket” notation for integrals involving operators. The presence of vertical bars distinguishes this use of angled brackets from that on the left-hand side of the equations. Note that a and aˆ are taken as equivalent.

92 Quantum physics

Dirac notation

	anm = ψnaψˆ m dx				n,m	eigenvector indices
				(4.31)	anm	matrix element
Matrix elementa				(4.31)	ψn	basis states
	= n\|aˆ\|m			(4.32)	aˆ	operator
					x	spatial coordinate
Bra vector	bra state vector = n\|			(4.33)	·\|	bra

Ket vector	ket state vector = \|m			(4.34)	\|·	ket

Scalar product	n\|m = ψnψm dx			(4.35)
Expectation	if Ψ = n cnψn			(4.36)	Ψ	wavefunction
					cn	probability amplitudes
	then	a =	c cmanm	(4.37)	cn	probability amplitudes
			n
		m	n

aThe Dirac bracket, n|aˆ|m , can also be written ψn|aˆ|ψm .

4.3 Wave mechanics

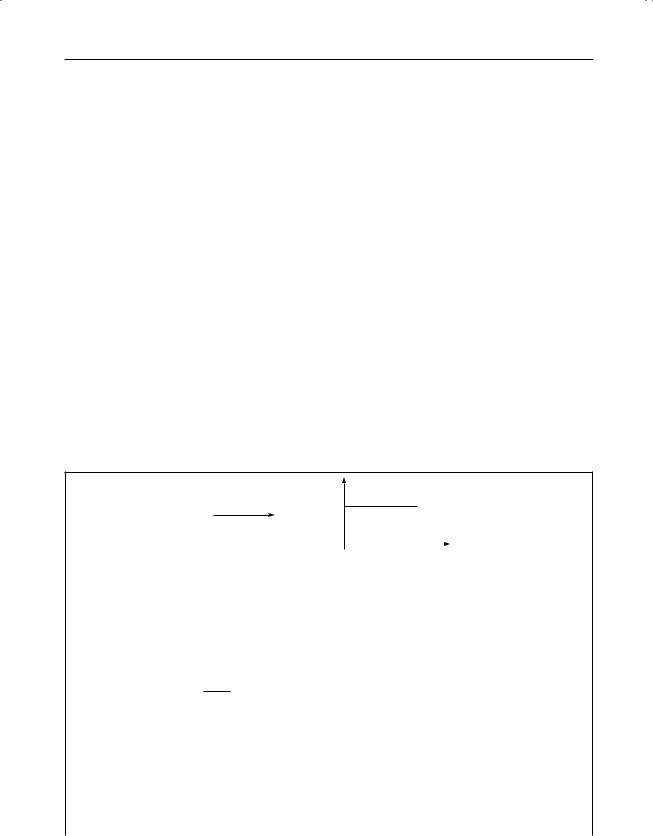
Potential stepa

V (x)

incident particle

Potential

0 (x < 0)

particle potential energy

step height

function

V (x) = "V0

(4.38)

≥

¯h 0

(Planck constant)/(2π)

Wavenumbers

¯h2k2 = 2mE

(x < 0)

(4.39)

k,q

particle wavenumbers

¯h2q2 = 2m(E − V0)

(x > 0)

(4.40)

particle mass

total particle energy

Amplitude

k − q

amplitude reﬂection

reﬂection

r =

(4.41)

coe cient

k + q

Amplitude

amplitude transmission

transmission

t =

(4.42)

k + q

coe cient

ji =

¯hk

(1 − |r|2)

(4.43)

Probability

particle ﬂux in zone i

currentsb

jii =

¯hq

|t|2

(4.44)

jii

particle ﬂux in zone ii

aOne-dimensional interaction with an incident particle of total energy E = KE + V . If E < V0 then q is imaginary

and		\|	r	2	= 1. 1	/	q	\| is then a measure of the tunnelling depth.
b			\|			\|
	Particle ﬂux with the sign of increasing x.

4.3 Wave mechanics	93

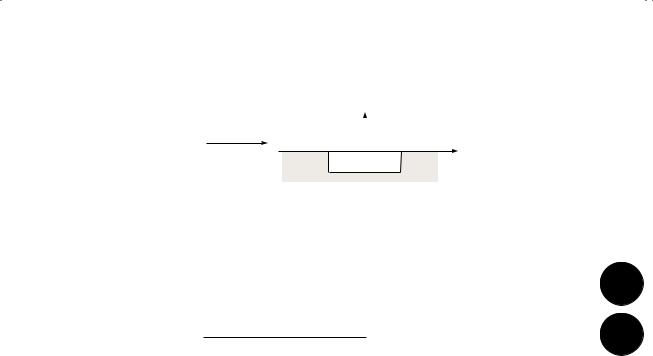
Potential wella

incident particle

V (x)

−a ii

a iii

−V0

V (x) = "0

particle potential energy

Potential

( x

> a)

well depth

function

(|x|

(4.45)

¯h

(Planck constant)/(2π)

−

| | ≤

well width

¯h

= 2mE

(|x| > a)

(4.46)

k,q

particle wavenumbers

Wavenumbers

particle mass

¯h2q2 = 2m(E + V0)

(|x| < a)

(4.47)

total particle energy

Amplitude

ie−2ika(q2

−

k2)sin2qa

amplitude reﬂection

reﬂection

r =

(4.48)

+ k

)sin2qa

coe cient

2kqcos2qa− i(q

Amplitude

2kqe−2ika

amplitude transmission

transmission

(4.49)

t = 2kqcos2qa− i(q2 + k2)sin2qa

coe cient

ji =

¯hk

(1 − |r|2)

(4.50)

Probability

particle ﬂux in zone i

currentsb

jiii =

¯hk

|t|2

(4.51)

jiii

particle ﬂux in zone iii

Ramsauer

n2¯h2π2

integer > 0

e ectc

En =

−V0 +

(4.52)

Ramsauer energy

8ma2

tanqa = "|

k /q

even parity

Bound states

|q/

odd parity

(4.53)

(V0 < E < 0)d

− |

q2 − |k|2 = 2mV0/¯h2

(4.54)

aOne-dimensional interaction with an incident particle of total energy E = KE + V > 0.

bParticle ﬂux in the sense of increasing x.

dIncident energy for which 2qa = nπ, |r| = 0, and |t| = 1.

When E < 0, k is purely imaginary. |k|

and q are obtained by solving these implicit equations.

94 Quantum physics

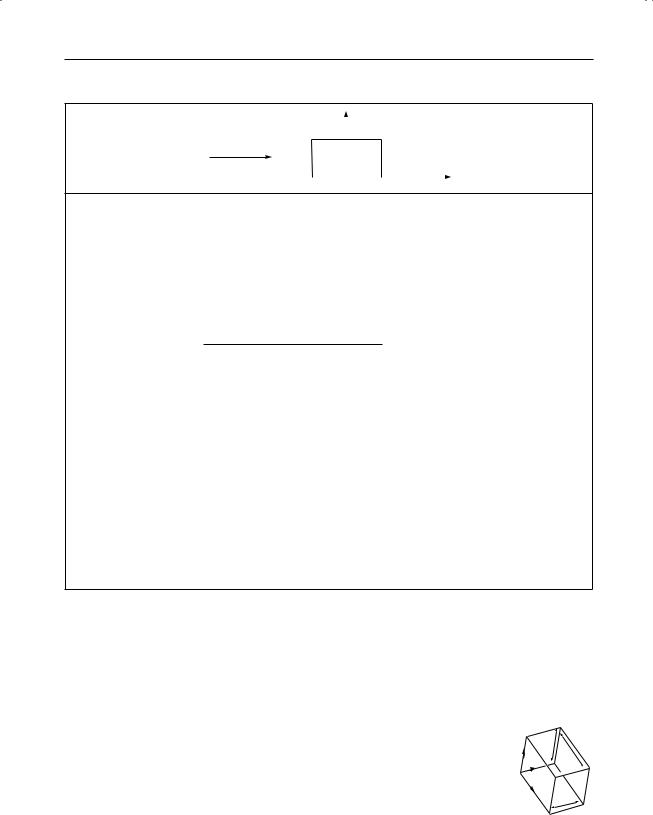
Barrier tunnellinga

incident particle		V (x)		V0
		V (x)


	i	ii		iii

	−a	0	a	x

Potential

( x

> a)

(4.55)

function

V (x) = "V0

(|x|

| | ≤

Wavenumber

¯h

= 2mE

(|x| > a)

(4.56)

and tunnelling

constant

¯h2κ2 = 2m(V0 − E)

(|x| < a)

(4.57)

Amplitude

r =

−

ie−2ika(k2

+ κ2)sinh2κa

reﬂection

coe cient

2kκcosh2κa− i(k

− κ

)sinh2κa

(4.58)

Amplitude

2kκe−2ika

transmission

(4.59)

t = 2kκcosh2κa− i(k2 − κ2)sinh2κa

coe cient

|t|2 =

4k2κ2

(4.60)

Tunnelling

(k2 + κ2)2 sinh2 2κa+ 4k2κ2

16k2κ2

probability

exp(−4κa)

(|t|2 1)

(k2 + κ2)2

(4.61)

ji =

¯hk

(1 − |r|2)

(4.62)

Probability

currentsb

jiii =

¯hk

|t|2

(4.63)

Vparticle potential energy

V0	well depth
¯h	(Planck constant)/(2π)
2a	barrier width

kincident wavenumber

κtunnelling constant

mparticle mass

Etotal energy (< V0)

ramplitude reﬂection coe cient

tamplitude transmission coe cient

|t|2 tunnelling probability

ji	particle ﬂux in zone i
jiii	particle ﬂux in zone iii

aBy a particle of total energy E = KE + V , through a one-dimensional rectangular potential barrier height V0 > E. bParticle ﬂux in the sense of increasing x.

Particle in a rectangular boxa

Eigen-

1/2

lπx

mπy

nπz

Ψlmn

eigenfunctions

functions

Ψlmn =

sin

a,b,c

box dimensions

abc

(4.64)

l,m,n

integers ≥ 1

Energy

Elmn

energy

Planck

Elmn =

(4.65)

levels

constant

particle mass

Density of

4π

(2M3E)1/2 dE

ρ(E)

density of

ρ(E) dE =

(4.66)

states (per unit

states

volume)

aSpinless particle in a rectangular box bounded by the planes x = 0, y = 0, z = 0, x = a, y = b, and z = c. The potential is zero inside and inﬁnite outside the box.

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 1415 / 3515 16 17 18 19 20 21 22 23 24 25 26 27 > Следующая >>>

Chapter 4 Quantum physics

4.1 Introduction

4.3 Wave mechanics