Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

Файл:

General Physics part 1 / PhysPraktikum / Woan G. The Cambridge Handbook of Physics Formulas (CUP, 2000)(ISBN 0521573491)(230s)_PRef_.pdf

Скачиваний:

Добавлен:

27.03.2015

Размер:

1.65 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 3513 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

74	Dynamics and mechanics

3.5Rigid body dynamics

Moment of inertia tensor

Moment of

Iij = (r2δij − xixj ) dm

(3.136)

r2 = x2 + y2 + z2

inertia tensora

δij

Kronecker delta

I = %

(y2 + z2) dm

− xy dm

− xz dm

moment of inertia

tensor

− xy dm

(x2%+ z2) dm

−% yz dm

mass element

% xz dm

yz dm

(x2%+ y2) dm

position vector of

− %

(3.137)

Iij

components of I

I12 = I12 − ma1a2

(3.138)

Iij

tensor with respect

Parallel axis

to centre of mass

I11 = I11 + m(a22 + a32)

(3.139)

ai,a

position vector of

theorem

Iij = Iij + m(|a|2δij − aiaj )

(3.140)

centre of mass

mass of body

Angular

J = Iω

(3.141)

angular momentum

momentum

angular velocity

Rotational

kinetic energy

T = 2 ω · J = 2 Iij ωiωj

(3.142)

aIii are the moments of inertia of the body. Iij

(i = j) are its products of inertia. The integrals are over the body

volume.

Principal axes

Principal

I =

principal moment of

inertia tensor

moment of

(3.143)

principal moments of

inertia tensor

inertia

angular momentum

Angular

J = (I1ω1,I2ω2,I3ω3)

(3.144)

ωi

components of ω

momentum

along principal axes

Rotational

T =

(I1ω12 + I2ω22 + I3ω32)

(3.145)

kinetic energy

Moment of

T = T (ω1,ω2,ω3)

(3.146)

inertia

Ji =

∂T

(J is ellipsoid surface)

(3.147)

ellipsoida

∂ωi

Perpendicular

≥ I3

generally

I1 + I2

(3.148)

axis theorem

to 3-axis

"= I3

ﬂat lamina

lamina

I1 = I2 = I3

asymmetric top

Symmetries

I1 = I2 = I3

symmetric top

(3.149)

I1 = I2 = I3

spherical top

aThe ellipsoid is deﬁned by the surface of constant T .

3.5 Rigid body dynamics	75

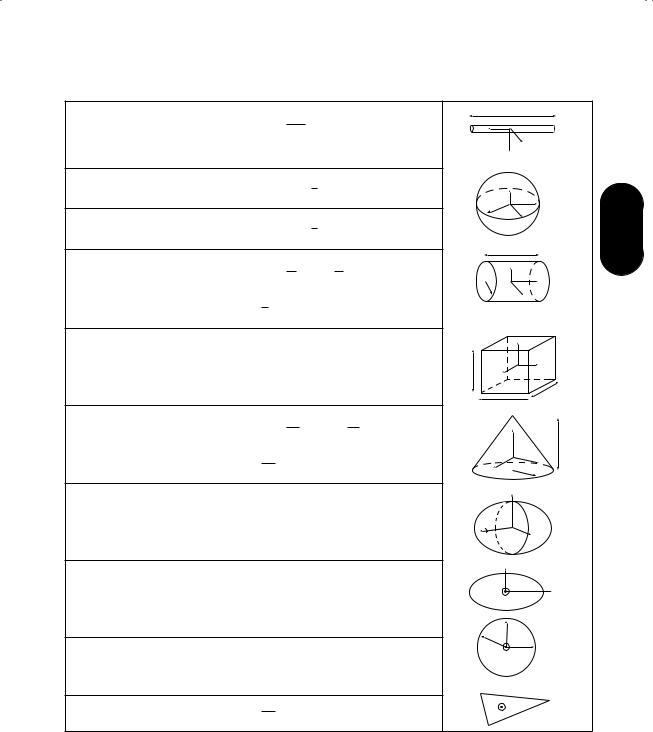
Moments of inertiaa

I1 = I2 =

ml2

(3.150)

Thin rod, length l

I3 0

(3.151)

Solid sphere, radius r

I1 = I2 = I3 = 5 mr

(3.152)

Spherical shell, radius r

I1 = I2 = I3 = 3 mr

(3.153)

Solid cylinder, radius r,

I1 = I2 =

4 r2 + l3

(3.154)

length l

I3 = 1 mr2

(3.155)

I1 = m(b2 + c2)/12

(3.156)

Solid cuboid, sides a,b,c

)/12

(3.157)

I2 = m(c

+ a

I3 = m(a2 + b2)/12

(3.158)

Solid circular cone, base

I1 = I2 =

20 m r2 +

(3.159)

radius r, height hb

I3 = 10 mr2

(3.160)

Solid ellipsoid, semi-axes

I1 = m(b2 + c2)/5

(3.161)

I2 = m(c2 + a2)/5

(3.162)

b I2

a,b,c

I3 = m(a2 + b2)/5

(3.163)

I1 = mb2/4

(3.164)

Elliptical lamina,

I2 = ma2/4

(3.165)

semi-axes a,b

I3 = m(a2 + b2)/4

(3.166)

Disk, radius r

I1 = I2 = mr2/4

(3.167)

I3 = mr2/2

(3.168)

I3 = m (a2 + b2 + c2)

Triangular platec

(3.169)

aWith respect to principal axes for bodies of mass m and uniform density. The radius of gyration is deﬁned as k = (I/m)1/2.

bOrigin of axes is at the centre of mass (h/4 above the base).

cAround an axis through the centre of mass and perpendicular to the plane of the plate.

76 Dynamics and mechanics

Centres of mass

Solid hemisphere, radius r

d = 3r/8

from sphere centre

(3.170)

Hemispherical shell, radius r

d = r/2

from sphere centre

(3.171)

Sector of disk, radius r, angle

sinθ

2θ

d =

from disk centre

(3.172)

Arc of circle, radius r, angle

sinθ

from circle centre

(3.173)

2θ

d = r

Arbitrary triangular lamina,

d = h/3

perpendicular from base

(3.174)

height ha

Solid cone or pyramid, height

d = h/4

perpendicular from base

(3.175)

Spherical cap, height h,

solid:

d =

(2r − h)2

from sphere centre

(3.176)

sphere radius r

shell:

4 3r − h

(3.177)

d = r − h/2 from sphere centre

Semi-elliptical lamina,

d =

from base

(3.178)

height h

3π

ah is the perpendicular distance between the base and apex of the triangle.

Pendulums

period

gravitational acceleration

Simple

P = 2π

θ02

+ · · ·

1 +

(3.179)

length

pendulum

θ0

maximum angular

displacement

Conical

P = 2π

l cosα

1/2

pendulum

(3.180)

cone half-angle

Torsional

lI0

1/2

moment of inertia of bob

torsional rigidity of wire

penduluma

P = 2π C

(3.181)

(see page 81)

P 2π

distance of rotation axis

(ma2 + I1 cos2 γ1

from centre of mass

m mass of body

Compound

mga

pendulumb

+ I2 cos2 γ2 + I3 cos2 γ3)

1/2

principal moments of

(3.182)

inertia

γi

angles between rotation

axis and principal axes

Equal

1/2

double

P 2π (2 ± √

2)g

(3.183)

pendulumc

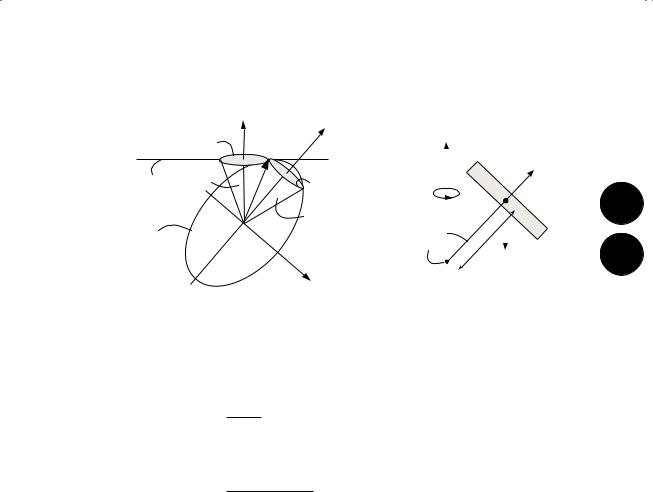
l θ0

l α

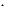
l I0

I1	a	I3
		I2

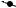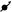
l m

aAssuming the bob is supported parallel to a principal rotation axis. bI.e., an arbitrary triaxial rigid body.

cFor very small oscillations (two eigenmodes).

3.5 Rigid body dynamics	77

Tops and gyroscopes

herpolhode

space

J 3

invariable

cone

polhode

Ωp

plane

body

moment

cone

of inertia

support point

ellipsoid

prolate symmetric top

gyroscope

G1 = I1ω˙1 + (I3 − I2)ω2ω3

(3.184)

rotation)

external couple (= 0 for free

Euler’s equationsa

G2 = I2ω˙2 + (I1 − I3)ω3ω1

(3.185)

principal moments of inertia

G3 = I3ω˙3 + (I2 − I1)ω1ω2

(3.186)

ωi

angular velocity of rotation

Free symmetric

Ωb =

I1 − I3

ω3

(3.187)

Ωb

body frequency

Ωs

space frequency

topb (I3 < I2 = I1)

Ωs =

(3.188)

total angular momentum

Free asymmetric

(I1

−

I3)(I2

−

I3)

top

Ωb2 =

I1I2

ω32

(3.189)

Ωp

precession angular velocity

Ω2 I

cosθ

−

ΩpJ3 + mga = 0

(3.190)

angle from vertical

Steady gyroscopic

p 1

(slow)

angular momentum around

Mga/J3

symmetry axis

precession

Ωp "J3/(I1 cosθ)

(fast)

(3.191)

mass

gravitational acceleration

distance of centre of mass

Gyroscopic

J32

≥

4I1mgacosθ

(3.192)

from support point

stability

moment of inertia about

support point

Gyroscopic limit

J32 I1mga

(3.193)

(“sleeping top”)

Nutation rate

Ωn = J3/I1

(3.194)

Ωn

nutation angular velocity

Gyroscope

Ωp =

mga

(1 − cosΩnt)

(3.195)

time

released from rest

aComponents are with respect to the principal axes, rotating with the body.

bThe body frequency is the angular velocity (with respect to principal axes) of ω around the 3-axis. The space frequency is the angular velocity of the 3-axis around J , i.e., the angular velocity at which the body cone moves around the space cone.

cJ close to 3-axis. If Ω2b < 0, the body tumbles.

78 Dynamics and mechanics

3.6 Oscillating systems Free oscillations

oscillating variable

Di erential

d2x

time

equation

+ 2γ

+ ω02x = 0

(3.196)

damping factor (per unit

dt2

mass)

ω0

undamped angular frequency

Underdamped

x = Ae−γt cos(ωt+ φ)

(3.197)

amplitude constant

solution (γ < ω0)

where

ω = (ω02 − γ2)1/2

(3.198)

phase constant

angular eigenfrequency

Critically damped

x = e−γt(A1 + A2t)

(3.199)

amplitude constants

solution (γ = ω0)

Overdamped

x = e−γt(A1eqt + A2e−qt)

(3.200)

solution (γ > ω0)

where

q = (γ2 − ω02)1/2

(3.201)

Logarithmic

∆ = ln

2πγ

(3.202)

∆

logarithmic decrement

decrementa

an+1

nth displacement maximum

Quality factor

Q =

ω0

if Q 1

(3.203)

quality factor

2γ

∆

aThe decrement is usually the ratio of successive displacement maxima but is sometimes taken as the ratio of successive displacement extrema, reducing ∆ by a factor of 2. Logarithms are sometimes taken to base 10, introducing a further factor of log10 e.

Forced oscillations

oscillating variable

Di erential

d2x

time

equation

+ 2γ

+ ω02x = F0eiωf t

(3.204)

dt2

damping factor (per unit

mass)

x = Aei(ωf t−φ),

where

(3.205)

ω0

undamped angular frequency

Steady-

A = F0[(ω2

−

ω2)2 + (2γωf )2]−1/2

(3.206)

force amplitude (per unit

mass)

state

F0/(2ω0)

(γ ωf )

(3.207)

ωf

forcing angular frequency

solutiona

[(ω0

−

ωf )2 + γ2]1/2

amplitude

tanφ =

2γωf

(3.208)

phase lag of response behind

ω02 − ωf2

driving force

Amplitude

−

ωar

amplitude resonant forcing

resonanceb

ωar = ω0

2γ

(3.209)

angular frequency

Velocity

ωvr = ω0

(3.210)

ωvr

velocity resonant forcing

resonancec

angular frequency

Quality

Q =

ω0

(3.211)

quality factor

factor

2γ

Impedance

Z = 2γ + i

ωf2 − ω02

(3.212)

impedance (per unit mass)

ωf

aExcluding the free oscillation terms.

bForcing frequency for maximum displacement.

cForcing frequency for maximum velocity. Note φ = π/2 at this frequency.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 3513 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>