Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

Файл:

General Physics part 1 / PhysPraktikum / Woan G. The Cambridge Handbook of Physics Formulas (CUP, 2000)(ISBN 0521573491)(230s)_PRef_.pdf

Скачиваний:

Добавлен:

27.03.2015

Размер:

1.65 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 358 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

32	Mathematics

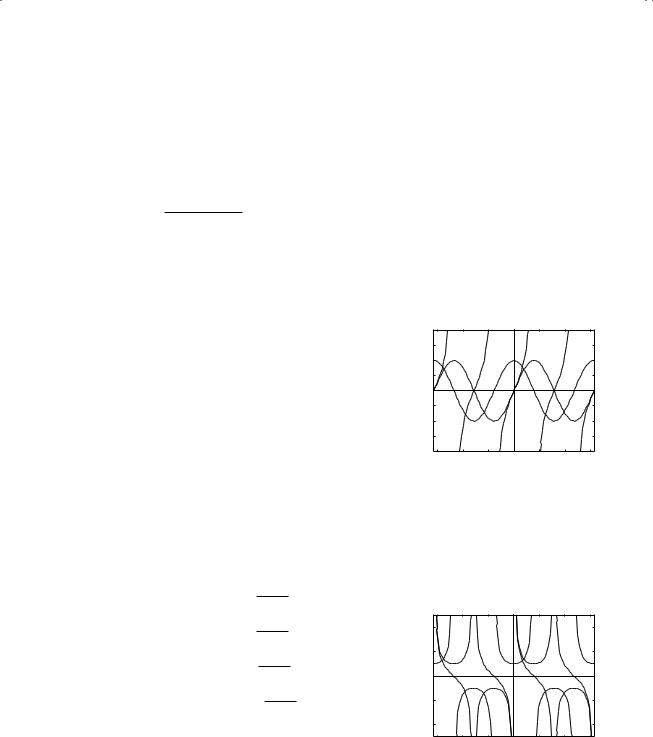
2.5Trigonometric and hyperbolic formulas

Trigonometric relationships

sin(A± B) = sinAcosB ± cosAsinB																				(2.171)
cos(A± B) = cosAcosB sinAsinB																				(2.172)
tan(A		±		B) =				tanA± tanB												(2.173)
		±						1		tanAtanB

cosAcosB =								1	[cos(A+ B) + cos(A− B)]											(2.174)

								2
sinAcosB =								1	[sin(A+ B) + sin(A− B)]											(2.175)

								2
sinAsinB =								1	[cos(A− B) − cos(A+ B)]											(2.176)

								2
cos2 A+ sin2 A = 1																				(2.177)
sec2 A− tan2 A = 1																				(2.178)
csc2 A− cot2 A = 1																				(2.179)

sin2A = 2sinAcosA																				(2.180)
cos2A = cos2 A− sin2 A																				(2.181)
tan2A =							2tanA													(2.182)
tan2A =						1 − tan2 A														(2.182)
sin3A = 3sinA− 4sin3 A																				(2.183)
cos3A = 4cos3 A− 3cosA																				(2.184)
sinA+ sinB = 2sin											A+ B				cos		A− B			(2.185)
sinA+ sinB = 2sin															cos		A− B			(2.185)
										2						2
sinA		−		sinB = 2cos								A+ B			sin		A− B			(2.186)
sinA				sinB = 2cos											sin		A− B			(2.186)
										2						2
cosA+ cosB = 2cos												A+ B			cos			A− B		(2.187)
cosA+ cosB = 2cos															cos			A− B		(2.187)
										2						2
cosA	−		cosB =						−	2sin			A+ B			sin			A− B	(2.188)
cosA			cosB =							2sin						sin			A− B	(2.188)
														2		2

cos2 A =					1		(1 + cos2A)													(2.189)
cos2 A =					2		(1 + cos2A)													(2.189)
					2
sin2 A =					1		(1 − cos2A)													(2.190)

					2
cos3 A =					1		(3cosA+ cos3A)													(2.191)
cos3 A =					4		(3cosA+ cos3A)													(2.191)
					4
sin3 A =					1		(3sinA− sin3A)													(2.192)

					4

2
1							x
						cos	x	sin
								x

0
−1						x
						x
−2						tan
−2	6	−	4	−	2		0	2	4	6
−		−		−			x
							x

4
			sec	x
			sec	csc
2			x	csc
2
		cot
		x
0
−2
−4
−6	−4	−2	0	2	4	6
			x

2.5 Trigonometric and hyperbolic formulas	33

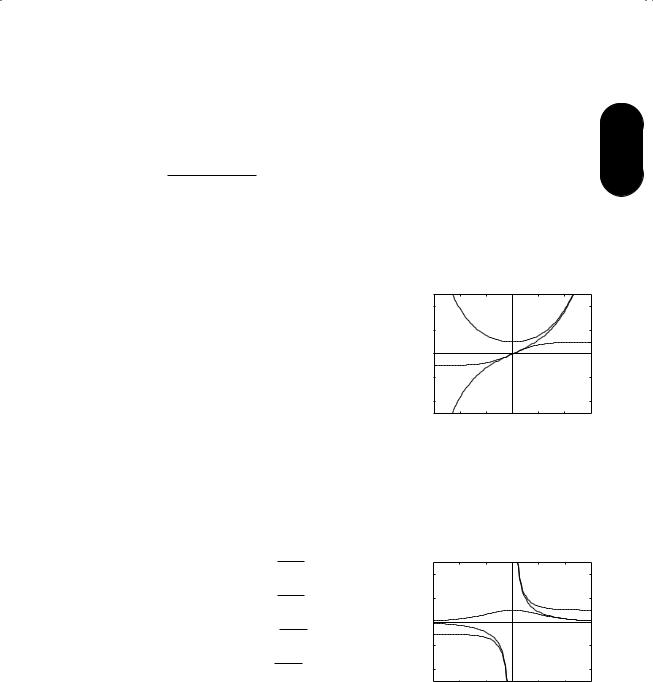
Hyperbolic relationshipsa

sinh(x± y) = sinhxcoshy ± coshxsinhy																			(2.193)
cosh(x± y) = coshxcoshy ± sinhxsinhy																			(2.194)
tanh(x		±		y) =				tanhx± tanhy											(2.195)
		±					1		±		tanhxtanhy
									±
coshxcoshy =									1	[cosh(x+ y) + cosh(x− y)]									(2.196)

									2
sinhxcoshy =									1	[sinh(x+ y) + sinh(x− y)]									(2.197)

									2
sinhxsinhy =									1	[cosh(x+ y) − cosh(x− y)]									(2.198)

									2

cosh2 x− sinh2 x = 1																			(2.199)
sech2 x+ tanh2 x = 1																			(2.200)
coth2 x− csch2 x = 1																			(2.201)
sinh2x = 2sinhxcoshx																			(2.202)
cosh2x = cosh2 x+ sinh2 x																			(2.203)
tanh2x =							2tanhx												(2.204)
tanh2x =						1 + tanh2 x													(2.204)
						1 + tanh2 x
sinh3x = 3sinhx+ 4sinh3 x																			(2.205)
cosh3x = 4cosh3 x− 3coshx																			(2.206)

sinhx+ sinhy = 2sinh												x+ y			cosh		x− y		(2.207)
sinhx+ sinhy = 2sinh															cosh		x− y		(2.207)
											2						2
sinhx		−		sinhy = 2cosh									x+ y		sinh		x− y		(2.208)
sinhx				sinhy = 2cosh											sinh		x− y		(2.208)
											2						2
coshx+ coshy = 2cosh													x+ y		cosh			x− y	(2.209)
coshx+ coshy = 2cosh															cosh			x− y	(2.209)
											2						2
coshx	−		coshy = 2sinh									x+ y		sinh		x− y			(2.210)
coshx			coshy = 2sinh											sinh		x− y			(2.210)
											2						2

cosh2 x =					1		(cosh2x+ 1)												(2.211)

					2
sinh2 x =					1		(cosh2x− 1)												(2.212)

					2
cosh3 x =					1		(3coshx+ cosh3x)												(2.213)

					4
sinh3 x =					1		(sinh3x− 3sinhx)												(2.214)

					4

4
		cosh
2			x
2
						tanhx
0
	tanhx
−2	sinh		x
−4	sinh
−4
−3	−2		−1	0	1	2	3
				x

4
2					cothx
		x			cothx
		x
		sech
0		csch
		csch
−2		x
−2
−4
−3	−2	−1	0	1	2	3
			x

aThese can be derived from trigonometric relationships by using the substitutions cosx →coshx and sinx →isinhx.

34 Mathematics

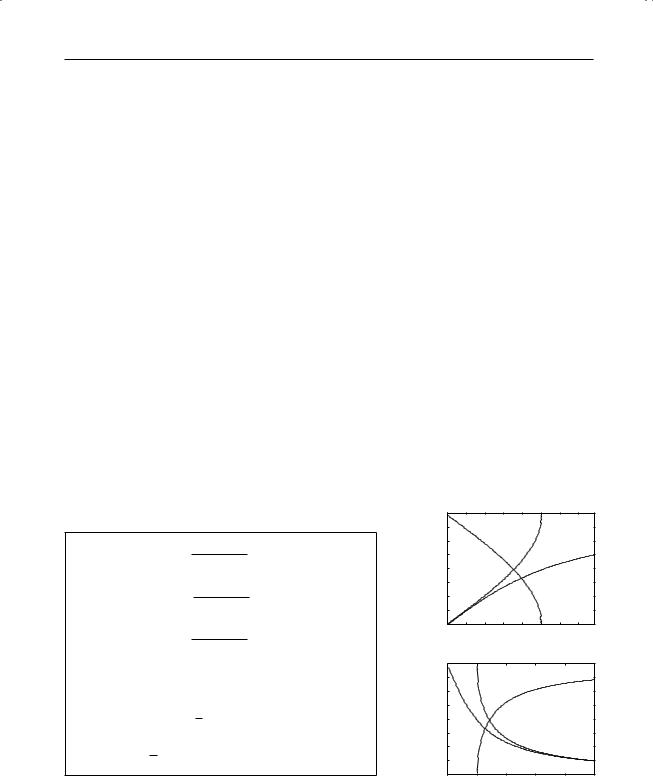
Trigonometric and hyperbolic deﬁnitions

de Moivre’s theorem				(cosx+ isinx)n = einx = cosnx+ isinnx					(2.215)

cosx =	1		eix + e−ix	(2.216)	coshx =	1		ex + e−x	(2.217)

	2					2
sinx =	1		eix − e−ix	(2.218)	sinhx =	1		ex − e−x	(2.219)

	2i					2
tanx =		sinx		(2.220)	tanhx =		sinhx		(2.221)
		cosx					coshx


cosix = coshx				(2.222)	coshix = cosx				(2.223)
sinix = isinhx				(2.224)	sinhix = isinx				(2.225)

cotx = (tanx)−1				(2.226)	cothx = (tanhx)−1				(2.227)
secx = (cosx)−1				(2.228)	sechx = (coshx)−1				(2.229)
cscx = (sinx)−1				(2.230)	cschx = (sinhx)−1				(2.231)

Inverse trigonometric functionsa						1.6
Inverse trigonometric functionsa								arccosx
		x						arccosx
arcsinx = arctan (1 − x2)1/2					(2.232)	1		x		arctanx
arccosx = arctan (1 − x			)		(2.233)			arcsin
		x2		1/2
arccscx = arctan (x2		11)1/2			(2.234)		0		x	1
	−					1.6	x	x
	−					1.6
arcsecx = arctan (x2 − 1)1/2					(2.235)		arccot arccsc			arcsecx
1						1
1
arccotx = arctan x					(2.236)
π
arccosx = 2 − arcsinx					(2.237)

aValid in the angle range 0 ≤ θ ≤ π/2. Note that arcsinx ≡ sin−1 x etc.

2.6 Mensuration	35

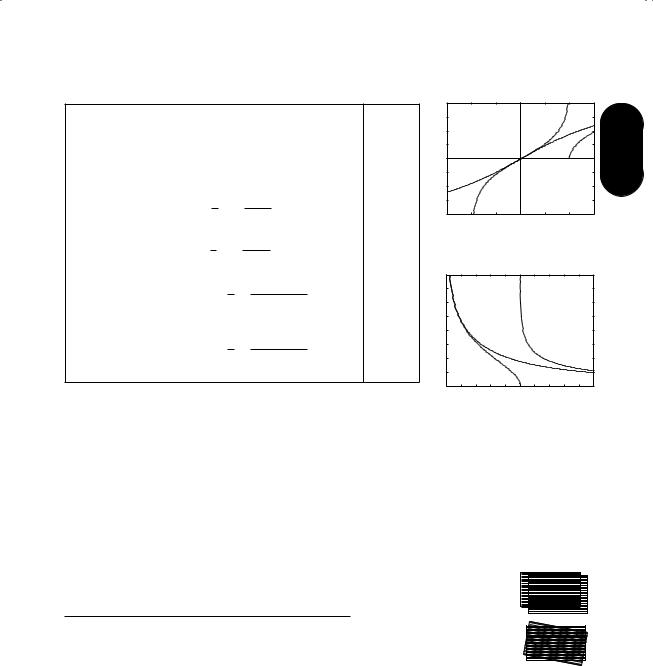
Inverse hyperbolic functions										2
arsinhx ≡ sinh−1 x = ln x+ (x2 + 1)1/2										2
arsinhx ≡ sinh−1 x = ln x+ (x2 + 1)1/2								(2.238)	for all x	1			artanhx		x	2
arcoshx ≡ cosh−1 x = ln x+ (x2 − 1)1/2								(2.239)	x ≥ 1	0		x		arcosh		2
	1	1 + x								−1	arsinh
artanhx ≡ tanh−1 x =	1	1 + x							\|x\| < 1	−2
artanhx ≡ tanh−1 x =	2 ln 1		−	x				(2.240)	\|x\| < 1	−2	−	1	0		1
	1		−								−		x
	1	x+ 1
arcothx ≡ coth−1 x =	2 ln x− 1							(2.241)	\|x\| > 1	4
	1				x2		1/2
arsechx ≡ sech−1 x = ln x		+ (1 − x				)		(2.242)	0 < x ≤ 1	3			arcoth
								(2.242)
										2
	1		(1 + x2)1/2							2			x
1	1		(1 + x2)1/2									arcsch
arcschx ≡ csch− x = ln x +												arcsch
arcschx ≡ csch− x = ln x +					x			(2.243)	x = 0	1		arsechx x
								(2.243)
										0			1			2
													x

2.6 Mensuration

Moire´ fringesa

Moire´ fringe spacing

Parallel pattern

dM =

−

(2.244)

d1,2

grating spacings

common grating

Rotational

dM =

(2.245)

spacing

patternb

2| sin(θ/2)|

relative rotation angle

(

| ≤

π/2)

aFrom overlapping linear gratings.

bFrom identical gratings, spacing d, with a relative rotation θ.

36	Mathematics

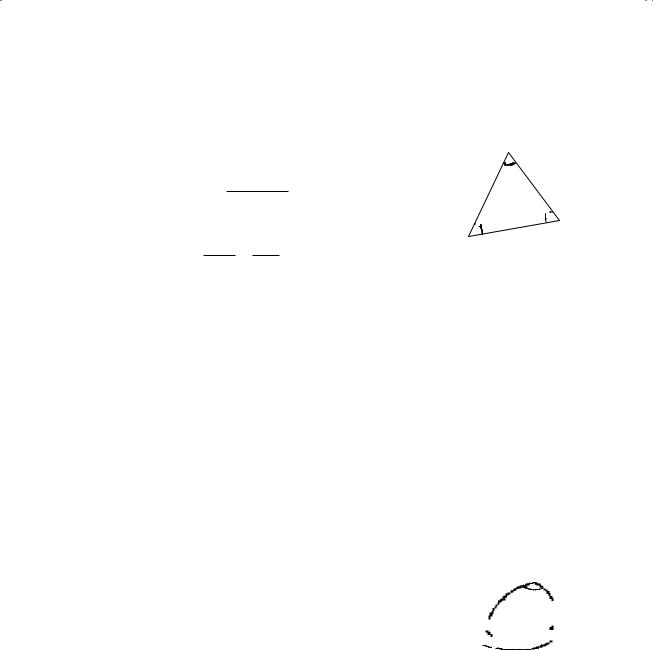
Plane triangles

Sine formulaa

(2.246)

sinA

sinB

sinC

a2 = b2 + c2 − 2bccosA

(2.247)

Cosine

cosA =

+ c − a

(2.248)

formulas

2bc

a = bcosC + ccosB

(2.249)

Tangent

tan

A− B

a− b

cot

(2.250)

formula

a+ b

area

absinC

(2.251)

sinB sinC

(2.252)

Area

sinA

= [s(s− a)(s− b)(s− c)]1/2

(2.253)

where s =

(a+ b+ c)

(2.254)

aThe diameter of the circumscribed circle equals a/sinA.

A B

Spherical trianglesa

Sine formula

sina

sinb

sinc

(2.255)

sinC

sinA

sinB

Cosine

cosa = cosbcosc+ sinbsinccosA

(2.256)

formulas

cosA = − cosB cosC + sinB sinC cosa

(2.257)

Analogue

sinacosB = cosbsinc− sinbcosccosA

(2.258)

formula

Four-parts

cosacosC = sinacotb− sinC cotB

(2.259)

formula

Areab

E = A+ B + C − π

(2.260)

aOn a unit sphere.

bAlso called the “spherical excess.”

2.6 Mensuration	37

Perimeter, area, and volume

Perimeter of circle

P = 2πr

(2.261)

Area of circle

A = πr2

(2.262)

Surface area of spherea

A = 4πR2

(2.263)

Volume of sphere

V =

πR3

(2.264)

P = 4aE(π/2, e)

(2.265)

Perimeter of ellipse

a2 + b2

1/2

2π

(2.266)

Area of ellipse

A = πab

(2.267)

Volume of ellipsoidc

abc

(2.268)

V = 4π

Surface area of

A = 2πr(h+ r)

(2.269)

cylinder

Volume of cylinder

V = πr2h

(2.270)

Area of circular coned

A = πrl

(2.271)

Volume of cone or

V = Abh/3

(2.272)

pyramid

Surface area of torus

A = π2(r1 + r2)(r2 − r1)

(2.273)

Volume of torus

π2

V = 4 (r2 − r1 )(r2 − r1)

(2.274)

Aread of spherical cap,

A = 2πRd

(2.275)

depth d

Volume of spherical

V = πd2

cap, depth d

−

(2.276)

Solid angle of a circle

Ω = 2π 1 − (z2 + r2)1/2

(2.277)

from a point on its

axis, z from centre

= 2π(1 − cosα)

(2.278)

Pperimeter

rradius

A area

Rsphere radius

Vvolume

asemi-major axis

bsemi-minor axis

Eelliptic integral of the second kind (p. 45)

eeccentricity (= 1 − b2/a2)

cthird semi-axis

hheight

lslant height

Ab base area

r1	inner radius
r2	outer radius

dcap depth

Ωsolid angle

zdistance from centre

αhalf-angle subtended

α	r
α
z

aSphere deﬁned by x2 + y2 + z2 = R2.

exact when e = 0 and e

0.91, giving a maximum error of 11% at e = 1.

c The approximation is

+ y

+ z

2 2

Ellipsoid deﬁned by x

= 1.

dCurved surface only.

38							Mathematics
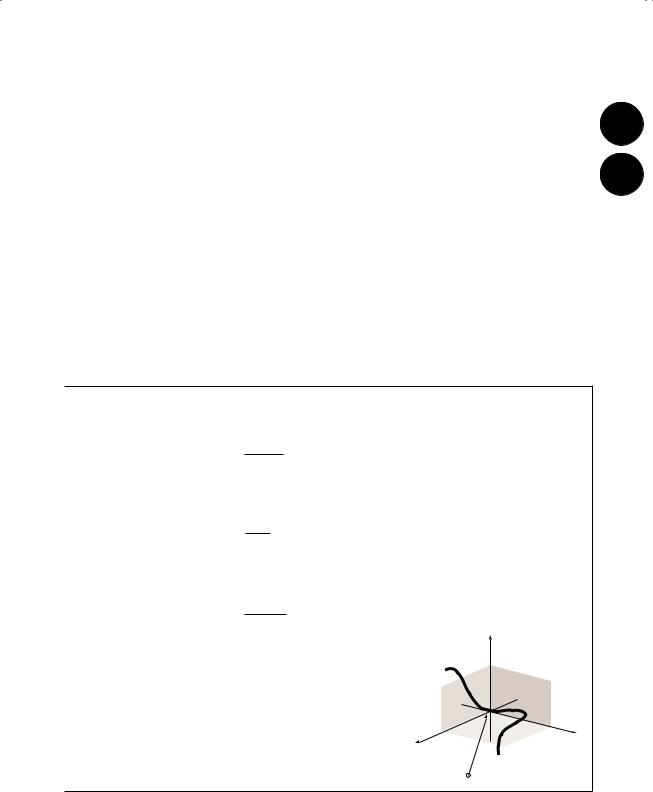
Conic sections
y					y		y
				b
	a		x		x		x
	a				a		a
							a

	parabola			ellipse		hyperbola
		2		x2	y2	x2	y2
equation	y		= 4ax	a2 + b2 = 1		a2 − b2 = 1
parametric		x = t2/(4a)		x = acost		x = ±acosht
form		y = t		y = bsint		y = bsinht

(±√

,0)

foci

(a,0)

a2 − b2

,0)

a2 + b2

√

+ b2

eccentricity

e = 1

−

e =

directrices

x = −a

x = ±

Platonic solidsa

solid	volume				surface area		circumradius					inradius
(faces,edges,vertices)
		a3√						a√				a√
			2								6					6
tetrahedron			2		a2√3						6					6
(4,6,4)		12			a2√3				4				12
(4,6,4)		12							4				12
								a√
cube	a3				6a2			a√			3	a
(6,12,8)
									2			2
									2			2
		a3√
		a3√	2					a					a
octahedron					2a2	√3		√					√
(8,12,6)	3
(8,12,6)	3									2					6
(12,30,20)					3a2	5(5 + 2√5)			√3(1 + √5)
	4						4					4						5
	4						4					4						5
dodecahedron		a3(15 + 7√5)						a				a					50 + 22√5
dodecahedron		a3(15 + 7√5)						a				a					50 + 22√5

(20,30,12)					5a2	√3			2(5 + √5)					√3 +
	12						4					4							3
	12			√5)			4					4							3
icosahedron		5a3(3 +						a				a							5
icosahedron		5a3(3 +						a				a							5

aOf side a. Both regular and irregular polyhedra follow the Euler relation, faces − edges + vertices = 2.

2.6 Mensuration	39

Curve measure

1/2

start point

Length of plane

end point

curve

l =

1 +

(2.279)

y(x)

plane curve

length

Surface of

1/2

revolution

A = 2π a

y 1 +

(2.280)

surface area

Volume of

V = π a

y2 dx

(2.281)

volume

revolution

Radius of

ρ = 1 +

3/2

d2y

−1

radius of

curvature

(2.282)

curvature

dx2

Di erential geometrya

Unit tangent	τˆ =	r˙	=	r˙			(2.283)

		\|r˙\|		v
Unit principal normal	nˆ =	r¨ − ˙vτˆ					(2.284)
		\|r¨ − ˙vτˆ \|
Unit binormal	ˆ						(2.285)
Unit binormal	b = τˆ×nˆ						(2.285)

		˙	r¨
Curvature	κ =	\|r×3\|					(2.286)
		\|r˙\|
Radius of curvature	ρ =	1					(2.287)
Radius of curvature	ρ =	κ					(2.287)
		κ

		r˙ · (r¨×		...
Torsion	λ =			r	)		(2.288)
Torsion	λ =						(2.288)
		\|r˙×r¨\|2
	˙						(2.289)
	τˆ = κvnˆ						(2.289)
Frenet’s formulas	˙					ˆ	(2.290)
Frenet’s formulas	nˆ = −κvτˆ +					λvb	(2.290)
	˙
	ˆ						(2.291)
	b = −λvnˆ						(2.291)

τtangent

rcurve parameterised by r(t)

v|r˙(t)|

nprincipal normal

bbinormal

κcurvature

ρradius of curvature

λ	torsion
		nˆ
		osculating
		plane
normal plane		τˆ
		τˆ
	r	rectifying
ˆ	r
ˆ		plane
b		plane

origin

aFor a continuous curve in three dimensions, traced by the position vector r(t).

40	Mathematics

2.7 Di erentiation

Derivatives (general)

Power

(un) = nun−1

(2.292)

Product

(uv) = u

+ v

(2.293)

Quotient

1 du

−

(2.294)

Function of a

[f(u)] =

[f(u)]

(2.295)

functiona

dnu

n dv dn−1u

[uv] = 0 v

+ 1

+ · · ·

Leibniz theorem

dxn

dxn−1

(2.296)

n dkv dn−ku

dnv

+ k

+ · · · + n u

dxk

dxn−k

dxn

Di erentiation

f(x) dx

= f(q)

(p constant)

(2.297)

under the integral

f(x) dx = −f(p)

sign

(q constant)

(2.298)

v(x)

General integral

u(x)

f(t) dt = f(v)

− f(u)

(2.299)

Logarithm

(logb |ax|) = (xlnb)−1

(2.300)

Exponential

(eax) = aeax

(2.301)

−

(2.302)

d2x

d2y

Inverse functions

−

(2.303)

dy2

dx2

d3x

d2y

dy d3y

−

(2.304)

dy3

dx2

dx3

npower index

u,v functions of x

f(u) function of u(x)

	n	binomial
	k	binomial
	k	coe cient

blog base

aconstant

aThe “chain rule.”

2.7 Di erentiation	41

Trigonometric derivativesa

(sinax) = acosax

(2.305)

(cosax) = −asinax

(2.306)

(tanax) = asec

(2.307)

(cscax) = −acscax· cotax

(2.308)

(secax) = asecax· tanax

(2.309)

(cotax) = −acsc2 ax

(2.310)

(arcsinax) = a(1 − a2x2)−1/2

(2.311)

(arccosax) = −a(1 − a2x2)−1/2

(2.312)

(arctanax) = a(1 + a2x2)−1

(2.313)

(arccscax) = −

(a2x2 − 1)−1/2

(2.314)

|ax|

(arcsecax) =

(a2x2

− 1)−1/2

(2.315)

(arccotax) = −a(a2x2 + 1)−1

(2.316)

aa is a constant.

Hyperbolic derivativesa

(sinhax) = acoshax

(2.317)

(coshax) = asinhax

(2.318)

(tanhax) = asech2 ax

(2.319)

(cschax) = −acschax· cothax

(2.320)

(sechax) = −asechax· tanhax

(2.321)

(cothax) = −acsch2 ax

(2.322)

(arsinhax) = a(a2x2 + 1)−1/2

(2.323)

(arcoshax) = a(a2x2 − 1)−1/2

(2.324)

(artanhax) = a(1 − a2x2)−1

(2.325)

(arcschax) = −

(1 + a2x2)−1/2

(2.326)

|ax|

(arsechax) =

−

a2x2)−1/2

)−

|ax|

(arcothax) = a(1 − a

(2.328)

(2.327)

aa is a constant.

42 Mathematics

Partial derivatives

Total

∂f

di erential

df =

dx+

dy +

(2.329)

f(x,y,z)

∂x

∂y

∂z

∂g

∂x

∂y

Reciprocity

∂x

∂y

∂g

x = −1

(2.330)

g(x,y)

∂f

∂x

∂f ∂y

∂f ∂z

Chain rule

(2.331)

∂u

∂z ∂u

∂x ∂u

∂y ∂u

∂x

Jacobian

∂u

∂v

∂w

∂(x,y,z)

∂y

u(x,y,z)

Jacobian

J =

(2.332)

∂(u,v,w)

∂u

∂v

∂w

v(x,y,z)

∂z

w(x,y,z)

∂u

∂v

∂w

Change of

)J dudvdw

volume in (x,y,z)

f(x,y,z) dxdydz =

f(u,v,w

volume in (u,v,w)

variable

(2.333)

mapped to by V

Euler–

I =

F(x,y,y

) dx

Lagrange

∂F

dy/dx

equation

then

δI = 0

when

(2.334)

a,b

ﬁxed end points

∂y

Stationary pointsa

saddle point

maximum

minimum

quartic minimum

Stationary point if

∂f

∂x = ∂y

= 0

at (x0,y0)

(necessary condition)

(2.335)

Additional su cient conditions

∂2f

∂2f ∂2f

∂2f

for maximum

< 0,

and

(2.336)

∂x2

∂x2 ∂y2

∂x∂y

∂2f

∂2f ∂2f

∂2f

for minimum

> 0,

and

(2.337)

∂x2

∂x2 ∂y2

∂x∂y

∂2f ∂2f

∂2f

for saddle point

∂x2 ∂y2

< ∂x∂y

∂2f2

(2.338)

aOf a function f(x,y) at the point (x0,y0). Note that at, for example, a quartic minimum

= 0.

∂x

∂y

2.7 Di erentiation	43

Di erential equations

Laplace

2f = 0

(2.339)

Di usiona

∂f

∂t = D

(2.340)

Helmholtz

2f + α2f = 0

(2.341)

Wave

1 ∂2f

f = c2 ∂t2

(2.342)

Legendre

− x2)

+ l(l + 1)y = 0

(2.343)

Associated

− x2)

+ l

(l + 1) −

y = 0

(2.344)

Legendre

1 − x2

Bessel

2 d2y

x dx2

+ x dx + (x − m )y = 0

(2.345)

Hermite

d2y

dx2 − 2x dx + 2αy = 0

(2.346)

Laguerre

d2y

x dx2 + (1 − x) dx + αy = 0

(2.347)

Associated

d2y

Laguerre

+ (1 + k − x)

+ αy = 0

(2.348)

dx2

Chebyshev

d2y

(1 − x ) dx2 − x dx + n y = 0

(2.349)

Euler (or

d2y

Cauchy)

+ ax

+ by = f(x)

(2.350)

dx2

Bernoulli

+ p(x)y = q(x)ya

(2.351)

Airy

d2y

dx2 = xy

(2.352)

ff(x,y,z)

D	di usion	2
	coe cient
α	constant

cwave speed

linteger

minteger

kinteger

ninteger

a,b constants

p,q functions of x

aAlso known as the “conduction equation.” For thermal conduction, f ≡ T and D, the thermal di usivity, ≡ κ ≡ λ/(ρcp), where T is the temperature distribution, λ the thermal conductivity, ρ the density, and cp the speciﬁc heat capacity of the material.

<<< < Предыдущая 1 2 3 4 5 6 78 / 358 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>