Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

Файл:

General Physics part 1 / PhysPraktikum / Woan G. The Cambridge Handbook of Physics Formulas (CUP, 2000)(ISBN 0521573491)(230s)_PRef_.pdf

Скачиваний:

Добавлен:

27.03.2015

Размер:

1.65 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 3512 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Chapter 3 Dynamics and mechanics

3.1Introduction

Unusually in physics, there is no pithy phrase that sums up the study of dynamics (the way in which forces produce motion), kinematics (the motion of matter), mechanics (the study of the forces and the motion they produce), and statics (the way forces combine to produce equilibrium). We will take the phrase dynamics and mechanics to encompass all the above, although it clearly does not!

To some extent this is because the equations governing the motion of matter include some of our oldest insights into the physical world and are consequentially steeped in tradition. One of the more delightful, or for some annoying, facets of this is the occasional use of arcane vocabulary in the description of motion. The epitome must be what Goldstein1 calls “the jabberwockian sounding statement” the polhode rolls without slipping on the herpolhode lying in the invariable plane, describing “Poinsot’s construction” – a method of visualising the free motion of a spinning rigid body. Despite this, dynamics and mechanics, including ﬂuid mechanics, is arguably the most practically applicable of all the branches of physics.

Moreover, and in common with electromagnetism, the study of dynamics and mechanics has spawned a good deal of mathematical apparatus that has found uses in other ﬁelds. Most notably, the ideas behind the generalised dynamics of Lagrange and Hamilton lie behind much of quantum mechanics.

1H. Goldstein, Classical Mechanics, 2nd ed., 1980, Addison-Wesley.

64 Dynamics and mechanics

3.2 Frames of reference Galilean transformations

									S
							r,r	position in frames S	S	m
Time and	r = r + vt					(3.1)		and S	S	m
positiona	t = t					(3.2)	v	velocity of S in S	r	r
							t,t	time in S and S		r
							t,t	time in S and S	vt
Velocity	u = u + v					(3.3)	u,u	velocity in frames S	vt
Velocity	u = u + v					(3.3)	u,u	velocity in frames S
								and S
	p = p + mv						p,p	particle momentum
Momentum	p = p + mv					(3.4)		in frames S and S
							m	particle mass

Angular	J = J + mr ×v + v×p t					(3.5)	J ,J	angular momentum
momentum	J = J + mr ×v + v×p t					(3.5)		in frames S and S
Kinetic	T = T + mu · v +	1		mv	2	(3.6)	T ,T	kinetic energy in
energy	T = T + mu · v +		2	mv		(3.6)		frames S and S

aFrames coincide at t = 0.

Lorentz (spacetime) transformationsa

−1/2

Lorentz factor

(3.7)

speed of light

γ = 1 − c2

velocity of S

Time and position

x = γ(x + vt );

x = γ(x

−

vt)

(3.8)

x,x

x-position in frames

y = y ;

y = y

(3.9)

S and S (similarly

z = z ;

z = z

(3.10)

t,t

for y and z)

t = γ t +

x !; t = γ t−

time in frames S and

(3.11)

Di erential

dX = (cdt,− dx,− dy,− dz)

spacetime four-vector

four-vectorb

(3.12)

aFor frames S and S coincident at t = 0 in relative motion along x. See page 141 for the transformations of electromagnetic quantities.

bCovariant components, using the (1,−1,−1,−1) signature.

S S

x x

Velocity transformationsa

Velocity

Lorentz factor

= [1 − (v/c)2]−1/2

ux =

ux + v

;

ux − v

(3.13)

1 + uxv/c2

velocity of S in S

1 − uxv/c2

speed of light

uy =

;

(3.14)

ui,ui

particle velocity

γ(1 + uxv/c

)

γ(1 − uxv/c

)

components in

uz =

;

(3.15)

frames S and S

x x

γ(1 + uxv/c2)

γ(1 − uxv/c2)

aFor frames S and S coincident at t = 0 in relative motion along x.

3.2 Frames of reference	65

Momentum and energy transformationsa

Momentum and energy

Lorentz factor

= [1 − (v/c)2]−1/2

γ(p

/c2);

= γ(p

−

vE/c2)

(3.16)

velocity of S in S

+ vE

py = py;

(3.17)

speed of light

py = py

px,px

x components of

pz = pz;

pz = pz

(3.18)

momentum in S and

E = γ(E

+ vp

);

E = γ(E

−

vpx)

(3.19)

E,E

S (sim. for y and z)

energy in S and S

−

p2c2 = E 2

−

p 2c2 = m2c4

(3.20)

(rest) mass

total momentum in S

momentum

Four-vector

P = (E/c,−px,−py,−pz)

(3.21)

four-vector

aFor frames S and S coincident at t = 0 in relative motion along x. bCovariant components, using the (1,−1,−1,−1) signature.

S S

x x 3

Propagation of lighta

Doppler

ν frequency received in S

(3.22)

arrival angle in S

e ect

ν = γ

1 + c cosα!

frequency emitted in S

Lorentz factor

cosθ + v/c

cosθ =

(3.23)

= [1 − (v/c)2]−1/2

1 + (v/c)cosθ

Aberrationb

velocity of S in S

cosθ =

cosθ − v/c

(3.24)

speed of light

θ,θ

emission angle of light

1 − (v/c)cosθ

in S and S

Relativistic

P (θ) =

sinθ

(3.25)

P (θ) angular distribution of

beamingc

2γ

[1 − (v/c)cosθ]

photons in S

aFor frames S and S coincident at t = 0 in relative motion along x.

bLight travelling in the opposite sense has a propagation angle of π + θ radians%.

cAngular distribution of photons from a source, isotropic and stationary in S . 0π P (θ) dθ = 1.

Sy c

Sy Sy

θ c x x

Four-vectorsa

Covariant and

= x

x1 = −x

covariant vector

contravariant

components

= −x2

x3 = −x3

(3.26)

contravariant components

Scalar product

xiyi = x0y0 + x1y1 + x2y2 + x3y3

(3.27)

xi,x i four-vector components in

Lorentz transformations

frames S and S

= γ[x 0 + (v/c)x 1

];

x 0

= γ[x0 − (v/c)x1]

(3.28)

Lorentz factor

= γ[x 1 + (v/c)x 0

];

x 1

= γ[x1

−

(v/c)x0

]

(3.29)

= [1 − (v/c)2]−1/2

= x 2;

x 3

= x3

(3.30)

velocity of S in S

speed of light

aFor frames S and S , coincident at t = 0 in relative motion along the (1) direction. Note that the (1,−1,−1,−1) signature used here is common in special relativity, whereas (−1,1,1,1) is often used in connection with general relativity (page 67).

66	Dynamics and mechanics

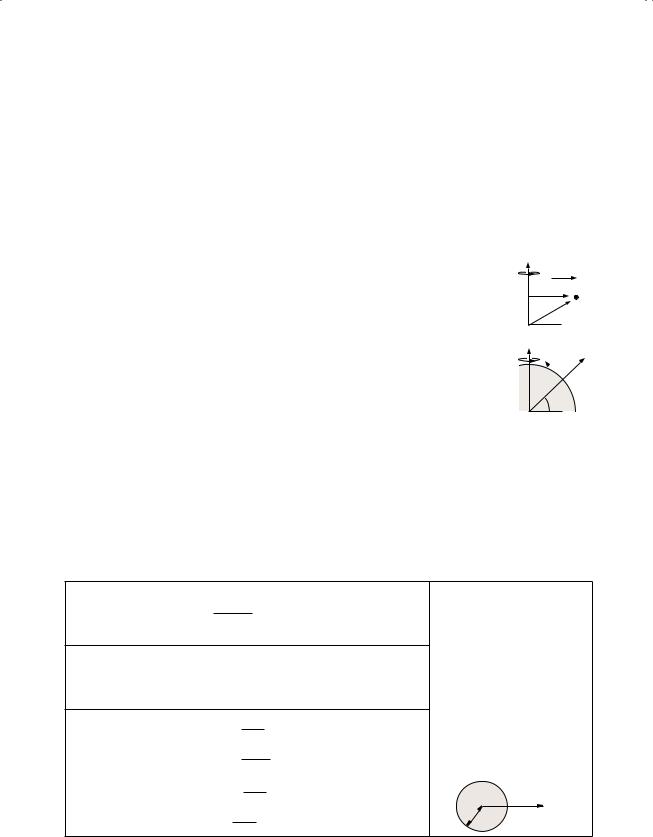
Rotating frames

any vector

Vector trans-

stationary frame

+ ω

(3.31)

rotating frame

formation

angular velocity

of S in S

˙v,˙v

accelerations in S

Acceleration

˙v = ˙v + 2ω×v + ω×(ω×r )

(3.32)

and S

velocity in S

position in S

Coriolis force

2mω

(3.33)

F cor coriolis force

−

particle mass

cor

Centrifugal

−

mω

(ω

r )

(3.34)

F cen centrifugal force

perpendicular to

cen

force

= +mω2r

(3.35)

particle from

rotation axis

mx¨ = Fx + 2mωe(y˙sinλ− ˙z cosλ)

nongravitational

Motion

(3.36)

force

latitude

relative to

my¨ = Fy − 2mωex˙ sinλ

(3.37)

northerly axis

Earth

local vertical axis

m¨z = Fz − mg + 2mωex˙ cosλ

(3.38)

easterly axis

Foucault’s

Ωf = −ωe sinλ

(3.39)

Ωf

pendulum’s rate

of turn

penduluma

ωe

Earth’s spin rate

aThe sign is such as to make the rotation clockwise in the northern hemisphere.

F cen

r m

ωe

y z

3.3 Gravitation

Newtonian gravitation

m1,2 masses

Newton’s law of

F 1 = Gm1m2 rˆ12

(3.40)

F 1

force on m1 (= −F 2)

gravitation

r12

vector from m1 to m2

unit vector

g = − φ

(3.41)

constant of gravitation

Newtonian ﬁeld

gravitational ﬁeld strength

equationsa

φ = − · g = 4πGρ

gravitational potential

(3.42)

mass density

vector from sphere centre

Fields from an

g(r) =

− r2

rˆ

(r > a)

(3.43)

mass of sphere

isolated

GMr rˆ

(r < a)

radius of sphere

uniform sphere,

− GM

mass M, r from

(r > a)

a M

the centre

φ(r) =

− r

(3.44)

GM (r2

3a2) (r < a)

−

aThe gravitational force on a mass m is mg.

3.3 Gravitation	67

General relativitya

Line element

ds2 = gµν dxµ dxν = − dτ2

(3.45)

Christo el

Γαβγ =

gαδ(gδβ,γ

+ gδγ,β − gβγ,δ)

(3.46)

symbols and

φ;γ = φ,γ ≡ ∂φ/∂xγ

(3.47)

covariant

(3.48)

di erentiation

A;γ

= A,γ

+ Γ βγA

Bα;γ = Bα,γ − ΓβαγBβ

(3.49)

Rαβγδ = ΓαµγΓµβδ − ΓαµδΓµβγ

+ Γαβδ,γ − Γαβγ,δ

(3.50)

Riemann tensor

Bµ;α;β − Bµ;β;α = RγµαβBγ

(3.51)

Rαβγδ = −Rαβδγ ;

Rβαγδ = −Rαβγδ

(3.52)

Rαβγδ + Rαδβγ + Rαγδβ = 0

(3.53)

Dvµ

Geodesic

= 0

(3.54)

Dλ

equation

DAµ

dAµ

where

≡

+ Γµαβ Aαvβ

(3.55)

Dλ

dλ

Geodesic

D2ξµ

deviation

= −Rµαβγvαξβvγ

(3.56)

Dλ2

Ricci tensor

Rαβ ≡ Rσασβ = gσδRδασβ = Rβα

(3.57)

Einstein tensor

µν

= R

− 2 g

(3.58)

Einstein’s ﬁeld

Gµν = 8πT µν

(3.59)

equations

Perfect ﬂuid

T µν = (p+ ρ)uµuν + pgµν

(3.60)

−1

Schwarzschild

= − 1 −

1 −

solution

(exterior)

+ r2(dθ2 + sin2 θ dφ2)

(3.61)

Kerr solution (outside a spinning black hole)

ds2 =

−

∆ − a2 sin2 θ

dt2

−

2Mrsin2 θ

dt dφ

(r2 + a2)2 −2a2∆sin2 θ

sin2 θdφ2 +

dr2

+ 2 dθ2

(3.62)

∆

ds	invariant interval
dτ	proper time interval
gµν	metric tensor
dxµ	di erential of xµ
Γα	Christo el symbols
βγ
,α	partial di . w.r.t. xα
;α	covariant di . w.r.t. xα
;α	covariant di . w.r.t. xα	3
φ	scalar
Aα	contravariant vector
Bα	covariant vector
Bα	covariant vector
Rα	Riemann tensor
βγδ

vµ	tangent vector
	(= dxµ/dλ)

λa ne parameter (e.g., τ for material particles)

ξµ	geodesic deviation
Rαβ	Ricci tensor
Gµν	Einstein tensor

RRicci scalar (= gµν Rµν )

T µν	stress-energy tensor

ppressure (in rest frame)

ρdensity (in rest frame)

uν	ﬂuid four-velocity

Mspherically symmetric mass (see page 183)

(r,θ,φ) spherical polar coords.

ttime

Jangular momentum (along z)

a≡ J/M

∆≡ r2 − 2Mr + a2

2	≡ r2 + a2 cos2 θ

General relativity

conventionally uses the (

−

1,1,1,1) metric signature and “geometrized units” in which G = 1 and

10−

c = 1. Thus, 1kg = 7.425

m etc. Contravariant indices are written as superscripts and covariant indices as

means (ds)

etc.

subscripts. Note also that ds

68 Dynamics and mechanics

3.4 Particle motion Dynamics deﬁnitionsa

					F	force
Newtonian force	F = m¨r = p˙			(3.63)	m	mass of particle
					r	particle position vector

Momentum	p = m˙r			(3.64)	p	momentum

Kinetic energy	T =	1	mv2	(3.65)	T	kinetic energy
Kinetic energy	T =		mv2	(3.65)
	2				v	particle velocity

Angular momentum	J = r×p			(3.66)	J	angular momentum

Couple (or torque)	G = r×F			(3.67)	G	couple

Centre of mass			N		R0	position vector of centre of mass
(ensemble of N			i=1 miri		mi	mass of ith particle
(ensemble of N	R0 = iN=1 mi			(3.68)	mi	mass of ith particle
particles)	R0 = iN=1 mi			(3.68)	ri	position vector of ith particle

aIn the Newtonian limit, v c, assuming m is constant.

Relativistic dynamicsa

			v2	−1/2		γ	Lorentz factor
Lorentz factor			v2	−1/2	(3.69)	c	speed of light
Lorentz factor	γ = 1 − c2				(3.69)	c	speed of light
						v	particle velocity
						p	relativistic momentum
Momentum	p = γm0v				(3.70)	p	relativistic momentum
Momentum	p = γm0v				(3.70)	m0	particle (rest) mass
						m0	particle (rest) mass

Force	F =	dp			(3.71)	F	force on particle
Force	F =	dt			(3.71)	t	time
		dt				t	time

Rest energy	Er = m0c2				(3.72)	Er	particle rest energy

Kinetic energy	T = m0c2(γ − 1)				(3.73)	T	relativistic kinetic energy
Total energy	E = γm0c2				(3.74)
Total energy	= (p2c2 + m02c4)1/2				(3.75)	E	total energy (= Er + T )
	= (p2c2 + m02c4)1/2				(3.75)

aIt is now common to regard mass as a Lorentz invariant property and to drop the term “rest mass.” The symbol m0 is used here to avoid confusion with the idea of “relativistic mass” (= γm0) used by some authors.

Constant acceleration

v = u+ at					(3.76)	u	initial velocity
v2 = u2 + 2as					(3.77)
						v	ﬁnal velocity

s = ut+		1		at2	(3.78)	t	time
		2				s	distance travelled

s =	u+ v				(3.79)	a	acceleration
			t
	2

3.4 Particle motion	69

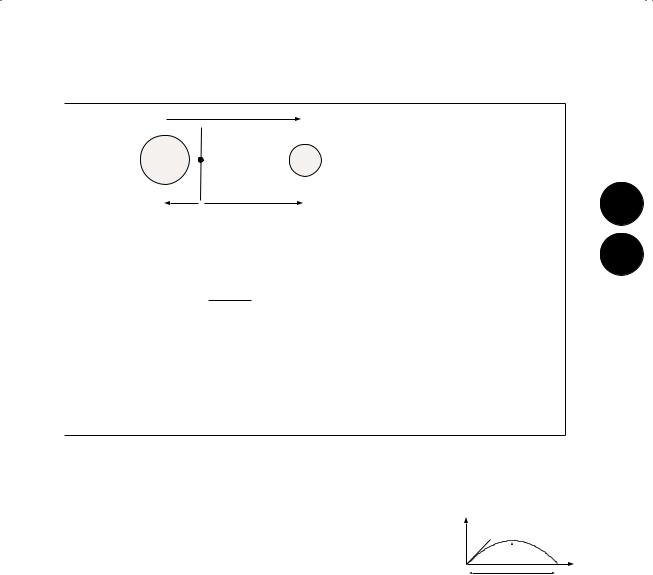
Reduced mass (of two interacting bodies)

centre

mass

Reduced mass

µ =

m1m2

(3.80)

m1 + m2

r1 =

(3.81)

Distances from

m1 + m2

centre of mass

r2 =

−m1

(3.82)

m1 + m2

Moment of

I = µ|r|

(3.83)

inertia

Total angular

J = µr×˙r

(3.84)

momentum

Lagrangian

L =

µ|˙r|2 − U(|r|)

(3.85)

µ	reduced mass	3
mi	interacting masses	3
ri	position vectors from centre of
ri	position vectors from centre of
	mass

rr = r1 − r2

|r| distance between masses

Imoment of inertia

Jangular momentum

LLagrangian

Upotential energy of interaction

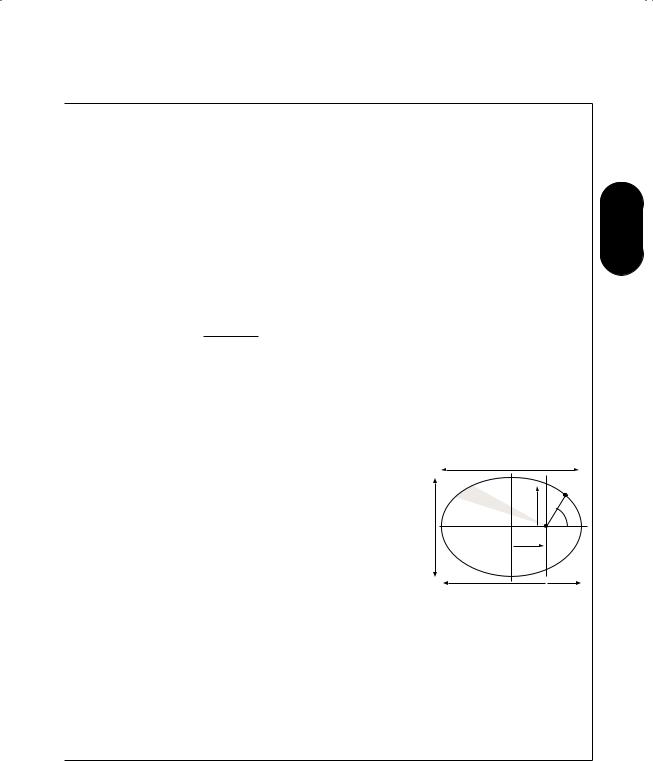
Ballisticsa

v = v0 cosαxˆ + (v0 sinα− gt)yˆ

initial velocity

velocity at t

Velocity

(3.86)

elevation angle

− 2gy

(3.87)

acceleration

= v0

gravitational

Trajectory

gx2

unit vector

y = xtanα− 2v02 cos2 α

(3.88)

time

Maximum

h =

v02

sin

(3.89)

maximum

height

Horizontal

l =

sin2α

(3.90)

range

aIgnoring the curvature and rotation of the Earth and frictional losses. g is assumed constant.

yˆ

α h xˆ

70	Dynamics and mechanics

Rocketry

Escape

vesc =

1/2

velocitya

(3.91)

Speciﬁc

Isp =

(3.92)

impulse

Exhaust

2γRTc

1/2

velocity (into

u = (γ − 1)µ

(3.93)

a vacuum)

Rocket

equation

∆v = uln Mf ≡ ulnM

(3.94)

(g = 0)

Multistage

ui lnMi

(3.95)

rocket

∆v =

i=1

In a constant

∆v = ulnM − gtcosθ

gravitational

(3.96)

ﬁeld

1/2

∆vah =

− 1

Hohmann

ra + rb

cotangential

(3.97)

1/2

transfer

∆vhb =

−

ra + rb

(3.98)

vesc	escape velocity

Gconstant of gravitation

Mmass of central body

rcentral body radius

Isp	speciﬁc impulse

ue ective exhaust velocity

gacceleration due to gravity

Rmolar gas constant

γratio of heat capacities

Tc	combustion temperature

µe ective molecular mass of exhaust gas

∆v	rocket velocity increment
Mi	pre-burn rocket mass
Mf	post-burn rocket mass

Mmass ratio

Nnumber of stages

Mi	mass ratio for ith burn
ui	exhaust velocity of ith burn

tburn time

θrocket zenith angle

∆vah	velocity increment, a to h
∆vhb	velocity increment, h to b
ra	radius of inner orbit
rb	radius of outer orbit
		transfer ellipse, h
	a	b

aFrom the surface of a spherically symmetric, nonrotating body, mass M.

bTransfer between coplanar, circular orbits a and b, via ellipse h with a minimal expenditure of energy.

3.4 Particle motion	71

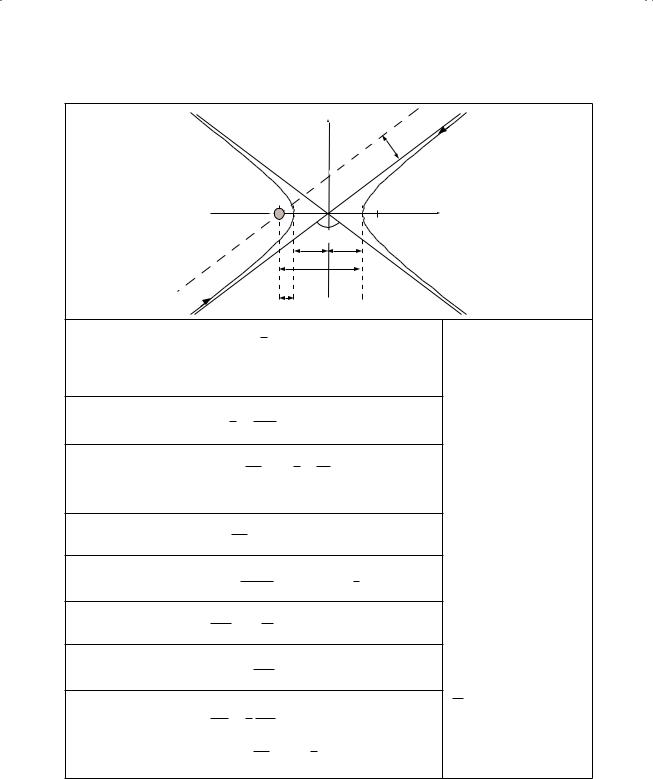
Gravitationally bound orbital motiona

Potential energy

GMm

of interaction

U(r) = −

≡ −

(3.99)

Total energy

E = − r + 2mr2 = − 2a

(3.100)

Virial theorem

E = U /2 = − T

(3.101)

(1/r potential)

U = −2 T

(3.102)

Orbital

= 1 + ecosφ ,

(3.103)

equation

(Kepler’s 1st

r =

a(1 − e2)

(3.104)

law)

1 + ecosφ

Rate of

sweeping area

= constant

(3.105)

(Kepler’s 2nd

law)

Semi-major axis

a =

(3.106)

2|E|

1 − e

Semi-minor axis

b =

(3.107)

(1 − e2)1/2

(2m|E|)1/2

EJ2

1/2

e = 1 +

= 1

Eccentricityb

−

(3.108)

mα2

Semi-latus-

rectum

r0 =

= a(1 − e2)

(3.109)

mα

Pericentre

rmin =

= a(1 − e)

(3.110)

1 + e

Apocentre

rmax =

= a(1 + e)

(3.111)

1 − e

Speed

v = GM

r − a

(3.112)

Period (Kepler’s

P = πα

1/2

m 1/2

3/2

= 2πa

3rd law)

2|E|3

(3.113)

U(r) potential energy

Gconstant of gravitation

Mcentral mass

morbiting mass ( M)

αGMm (for gravitation)

Etotal energy (constant)

J	total angular momentum
	(constant)	3
		3

Tkinetic energy

· mean value

r0 semi-latus-rectum

rdistance of m from M

eeccentricity

φphase (true anomaly)

Aarea swept out by radius vector (total area = πab)

asemi-major axis

bsemi-minor axis

	2a
A	m
A	r
	r0
	φ
	M

2b ae

rmax

rmin

rmin pericentre distance

rmax apocentre distance

vorbital speed

Porbital period

aFor an inverse-square law of attraction between two isolated bodies in the nonrelativistic limit. If m is not M, then the equations are valid with the substitutions m → µ = Mm/(M + m) and M → (M + m) and with r taken as the body separation. The distance of mass m from the centre of mass is then rµ/m (see earlier table on Reduced mass). Other orbital dimensions scale similarly, and the two orbits have the same eccentricity.

bNote that if the total energy, E, is < 0 then e < 1 and the orbit is an ellipse (a circle if e = 0). If E = 0, then e = 1 and the orbit is a parabola. If E > 0 then e > 1 and the orbit becomes a hyperbola (see Rutherford scattering on next page).

72	Dynamics and mechanics

Rutherford scatteringa

trajectory

for α < 0

scattering

centre

rmin (α<0)

trajectory

for α > 0

rmin (α>0)

Scattering potential

U(r) =

− r

(3.114)

U(r) potential energy

< 0

repulsive

particle separation

energy

α"> 0

attractive

(3.115)

constant

= |α|

scattering angle

Scattering angle

tan

(3.116)

total energy (> 0)

2Eb

impact parameter

rmin =

|α|

csc χ

−

(3.117)

rmin

closest approach

Closest approach

|α|

hyperbola semi-axis

= a(e± 1)

(3.118)

eccentricity

Semi-axis

a =

|α|

(3.119)

e =

E2b2

+ 1

1/2

Eccentricity

= csc

(3.120)

α2

Motion trajectoryb

4E2

x,y

position with respect to

α2

− b2 = 1

(3.121)

hyperbola centre

α2

1/2

Scattering centrec

x = ± 4E2 + b2

(3.122)

dσ

di erential scattering

dσ

1 dN

dΩ

cross section

Rutherford

dΩ

= n dΩ

(3.123)

beam ﬂux density

scattering formulad

4 χ

(3.124)

number of particles

4E !

csc

scattered into dΩ

Ω

solid angle

aNonrelativistic treatment for an inverse-square force law and a ﬁxed scattering centre. Similar scattering results from either an attractive or repulsive force. See also Conic sections on page 38.

bThe correct branch can be chosen by inspection. cAlso the focal points of the hyperbola.

dn is the number of particles per second passing through unit area perpendicular to the beam.

3.4 Particle motion	73

Inelastic collisionsa

m1 v1

m2 v2

Before collision

After collision

Coe cient of

− v1 = (v1 − v2)

(3.125)

coe cient of restitution

restitution

= 1

if perfectly elastic

(3.126)

pre-collision velocities

= 0

if perfectly inelastic

(3.127)

post-collision velocities

T ,T

total KE in zero

Loss of kinetic

−

= 1

−

(3.128)

momentum frame

before and after

energy

collision

m1 − m2

v1 +

(1 + )m2

(3.129)

Final velocities

m1 + m2

particle masses

m2 − m1

(1 + )m1

v2 +

(3.130)

m1 + m2

aAlong the line of centres, v1,v2 c. bIn zero momentum frame.

Oblique elastic collisionsa

								θ2 v2
		θ		m2			m1	m2
Before collision		θ		After collision			m1
	m1			v				θ
	m1							1
								v1
			m2 sin2θ				θ	angle between
	tanθ1 =		m2 sin2θ			(3.131)		centre line and
Directions of	tanθ1 =		− m2 cos2θ			(3.131)		centre line and
motion	m1		− m2 cos2θ			(3.132)	θi	incident velocity
	θ2 = θ					(3.132)	θi	ﬁnal trajectories
							mi	sphere masses
		> π/2		if m1 < m2
Relative	θ1 + θ2 = π/2			if m1 = m2		(3.133)
separation angle
	< π/2			if m1 > m2
	2		2		1/2
	v1 = (m1 + m2 − 2m1m2 cos2θ)				v	(3.134)	v	incident velocity
Final velocities			m1 + m2					of m1
Final velocities	2m1v							of m1
	2m1v						vi	ﬁnal velocities
	v2 = m1 + m2 cosθ					(3.135)

aCollision between two perfectly elastic spheres: m2 initially at rest, velocities c.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 3512 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>