Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

Файл:

General Physics part 1 / PhysPraktikum / Woan G. The Cambridge Handbook of Physics Formulas (CUP, 2000)(ISBN 0521573491)(230s)_PRef_.pdf

Скачиваний:

Добавлен:

27.03.2015

Размер:

1.65 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 356 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Chapter 2 Mathematics

2.1Notation

Mathematics is, of course, a vast subject, and so here we concentrate on those mathematical methods and relationships that are most often applied in the physical sciences and engineering.

Although there is a high degree of consistency in accepted mathematical notation, there is some variation. For example the spherical harmonics, Ylm, can be written Ylm, and there is some freedom with their signs. In general, the conventions chosen here follow common practice as closely as possible, whilst maintaining consistency with the rest of the handbook.

In particular:

scalars	a			general vectors	a
unit vectors	aˆ			scalar product	a · b
vector cross-product	a×b			gradient operator
	2					df
Laplacian operator				derivative			etc.
						dx
partial derivatives		∂f	etc.	derivative of r with	˙r
	∂x			respect to t
					L dl
nth derivative		dnf		closed loop integral
		dxn
closed surface integral	S		ds	matrix	A or aij
	x					n
mean value (of x)				binomial coe cient	r
factorial	!			unit imaginary (i2 = −1)	i
exponential constant	e			modulus (of x)	\|x\|
natural logarithm	ln			log to base 10	log10

20	Mathematics

2.2 Vectors and matrices

Vector algebra

Scalar producta

a · b = |a||b| cosθ

(2.1)

xˆ

yˆ

zˆ

a×b =

Vector productb

a b

sinθnˆ = ax

(2.2)

| || |

nˆ

(in)

a · b = b · a

(2.3)

Product rules

a×b = −b×a

(2.4)

a · (b + c) = (a · b) + (a · c)

(2.5)

a×(b + c) = (a×b) + (a×c)

(2.6)

Lagrange’s

(a×b) · (c×d ) = (a · c)(b · d ) − (a · d )(b · c)

(2.7)

identity

(a×b) c = bx

(2.8)

Scalar triple

product

(2.9)

= (b c)

a = (c a) b

= volume of parallelepiped

(2.10)

Vector triple

(a×b)×c = (a · c)b − (b · c)a

(2.11)

product

a×(b×c) = (a · c)b −

(a · b)c

(2.12)

a = (b

c)/[(a

(2.13)

b = (c

a)/[(a

(2.14)

Reciprocal vectors

(2.15)

c = (a

b)/[(a

(a · a) = (b · b) = (c · c) = 1

(2.16)

Vector a with

respect to a

a = (e1 · a)e1 + (e2 · a)e2 + (e3

· a)e3

(2.17)

nonorthogonal

basis {e1,e2,e3}c

Also known as the “dot product” or the “inner product.”

bAlso known as the “cross-product.” nˆ is a unit vector making a right-handed set with a and b. cThe prime ( ) denotes a reciprocal vector.

2.2 Vectors and matrices

Common three-dimensional coordinate systems

		point P
	θ
	r
		y
x	φ
x
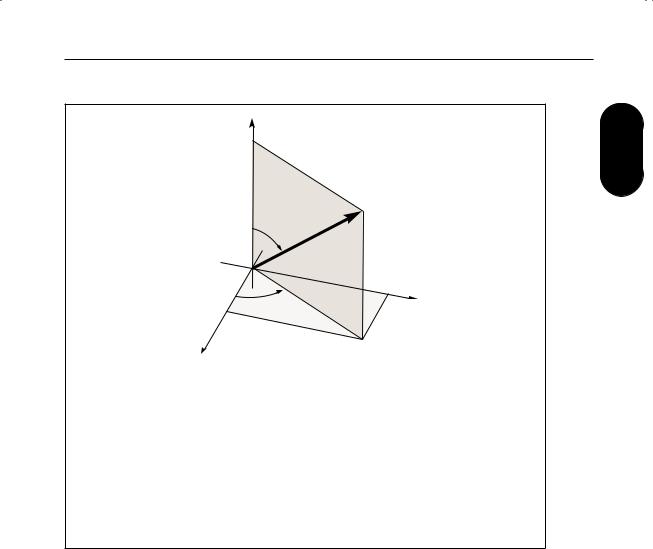
		ρ = (x2 + y2)1/2	(2.21)
x = ρcosφ = rsinθcosφ	(2.18)	r = (x2 + y2 + z2)1/2
y = ρsinφ = rsinθsinφ	(2.19)	r = (x2 + y2 + z2)1/2	(2.22)
y = ρsinφ = rsinθsinφ	(2.19)
z = rcosθ	(2.20)	θ = arccos(z/r)	(2.23)
z = rcosθ	(2.20)
		φ = arctan(y/x)	(2.24)

coordinate system:	rectangular	spherical polar	cylindrical polar
coordinates of P :	(x,y,z)	(r,θ,φ)	(ρ,φ,z)
volume element:	dx dy dz	r2 sinθ dr dθ dφ	ρ dρ dz dφ
metric elementsa (h1,h2,h3):	(1,1,1)	(1,r,rsinθ)	(1,ρ,1)

aIn an orthogonal coordinate system (parameterised by coordinates q1,q2,q3), the di erential line element dl is obtained from (dl)2 = (h1 dq1)2 + (h2 dq2)2 + (h3 dq3)2.

Gradient

Rectangular

f =

∂f

scalar ﬁeld

coordinates

xˆ +

yˆ

zˆ

(2.25)

∂x

∂y

∂z

unit vector

Cylindrical

f =

∂f

1 ∂f ˆ

∂f

distance from the

coordinates

ρˆ +

φ +

zˆ

(2.26)

z axis

∂ρ

∂φ

∂z

Spherical polar

f =

∂f

1 ∂f

∂f

coordinates

∂r

rˆ +

∂θ

θ +

rsinθ

∂φ

(2.27)

General

qˆ1

∂f

qˆ2

∂f

qˆ3

∂f

basis

orthogonal

f = h1 ∂q1

+ h2 ∂q2

+ h3 ∂q3

(2.28)

metric elements

coordinates

22 Mathematics

Divergence

Rectangular

∂Ax

∂Ay

∂Az

vector ﬁeld

A =

(2.29)

ith component

coordinates

∂x

∂y

∂z

of A

Cylindrical

· A =

1 ∂(ρAρ)

1 ∂Aφ

∂Az

distance from

coordinates

(2.30)

the z axis

∂ρ

ρ ∂φ

∂z

Spherical polar

1 ∂(r2Ar)

∂(Aθ sinθ)

∂Aφ

· A = r2

∂r

+ rsinθ

∂θ

+ rsinθ

∂φ

coordinates

(2.31)

General

A =

∂

(A1h2h3) +

∂

(A2h3h1)

h1h2h3

∂q1

∂q2

basis

orthogonal

(A3h1h2)

∂

metric

coordinates

(2.32)

elements

∂q3

Curl

xˆ

yˆ

zˆ

unit vector

Rectangular

A =

∂/∂x

∂/∂y

∂/∂z

(2.33)

vector ﬁeld

coordinates

ith component

of A

Cylindrical

ρˆ /ρ

zˆ/ρ

A =

∂/∂ρ

∂/∂φ

∂/∂z

(2.34)

distance from

coordinates

the z axis

Aρ

ρAφ

Spherical polar

rˆ

/(r

sinθ)

θ/(rsinθ)

φ/r

A =

∂/∂r

∂/∂θ

∂/∂φ

(2.35)

coordinates

rAθ

rAφ sin

General

qˆ1h1

qˆ2h2

qˆ3h3

basis

orthogonal

A =

∂/∂q

(2.36)

h h h

metric

coordinates

1 2

elements

h2A2

h3A3

h1A1

Radial formsa

(1/r) =

−r

(2.41)

r =

(2.37)

r31

· r = 3

(2.38)

· (r/r2) =

(2.42)

r2 = 2r

(2.39)

(1/r2) =

−2r

(2.43)

· (rr) = 4r

(2.40)

· (r/r3) = 4πδ(r)

(2.44)

aNote that the curl of any purely radial function is zero. δ(r) is the Dirac delta function.

2.2 Vectors and matrices	23

Laplacian (scalar)

Rectangular

∂2f

coordinates

f =

(2.45)

f scalar ﬁeld

∂x2

∂y2

∂z2

ρ distance

Cylindrical

∂

∂f

1 ∂2f

∂2f

f =

(2.46)

coordinates

∂ρ

ρ2

∂φ2

∂z2

z axis

from the

Spherical

∂

∂f

∂

∂f

∂2f

polar

2f =

sinθ

∂r

r2 sinθ

∂θ

r2 sin2 θ

∂φ2

coordinates

(2.47)

General

2f =

∂

h2h3 ∂f

∂

h3h1

∂f

∂q1

orthogonal

h1h2h3

h1 ∂q1

∂q2

qi basis

∂

h1h2

∂f

hi metric

coordinates

(2.48)

elements

∂q3

Di erential operator identities

(fg) ≡ f g + g f

(2.49)

· (fA) ≡ f · A + A · f

(2.50)

×(fA) ≡ f ×A + ( f)×A

(2.51)

(A · B) ≡ A×( ×B) + (A · )B + B×( ×A) + (B · )A

(2.52)

· (A×B) ≡ B · ( ×A) − A · ( ×B)

(2.53)

f,g

scalar ﬁelds

×(A×B) ≡ A( · B) − B( · A) + (B · )A − (A · )B

(2.54)

A,B

vector ﬁelds

· ( f) ≡ 2f ≡ f

(2.55)

×( f) ≡ 0

(2.56)

· ( ×A) ≡ 0

(2.57)

×( ×A) ≡ ( · A) − 2A

(2.58)

Vector integral transformations

Gauss’s

V ( · A) dV = Sc A · ds

vector ﬁeld

volume element

(Divergence)

(2.59)

closed surface

theorem

volume enclosed

S ( ×A) · ds = L A · dl

surface

Stokes’s

(2.60)

surface element

theorem

loop bounding S

line element

Green’s ﬁrst

S (f g) · ds = V · (f g) dV

(2.61)

f,g

scalar ﬁelds

theorem

= V [f 2g + ( f) · ( g)] dV

(2.62)

Green’s second

S [f( g) − g( f)] · ds = V (f g − g f) dV

theorem

(2.63)

k aikbkj .

24 Mathematics

Matrix algebraa

		a11	a12	· · ·	a1n
		a21	a22	· · ·	a2n		A	m by n matrix
Matrix deﬁnition		A = ...	...	· · · ...		(2.64)	aij	matrix elements
			a	· · ·	a
		a	a	· · ·	a
		m1	m2		mn
Matrix addition		C = A + B	if	cij = aij + bij		(2.65)
Matrix		C = AB if	cij = aikbkj			(2.66)
Matrix		(AB)C = A(BC)				(2.67)
multiplication		(AB)C = A(BC)				(2.67)
multiplication		A(B + C) = AB + AC				(2.68)
		A(B + C) = AB + AC				(2.68)

Transpose matrix	b	a˜ij = aji				(2.69)	˜aij	transpose matrix
	b						˜aij	transpose matrix
			˜	˜ ˜		(2.70)		(sometimes aijT , or aij )
		(AB...N) = N...BA				(2.70)
								complex conjugate (of
Adjoint matrix		A† = A˜				(2.71)		each component)
(deﬁnition 1)c		(AB...N)† = N† ...B†A†				(2.72)	†	adjoint (or Hermitian
								conjugate)
							H	Hermitian (or
Hermitian matrixd		H† = H				(2.73)	H	Hermitian (or
								self-adjoint) matrix

examples:

A =	a11		a12	a13
A =		a21	a22	a23
	a31		a32	a33
A˜ =		a11	a21	a31
A˜ =	a12		a22	a32

	a13		a23	a33

	b11	b12	b13
B =	b21	b22	b23

	b31	b32	b33
	a11 + b11		a12 + b12	a13	+ b13
A + B =	a21 + b21		a22 + b22	a23	+ b23

	a31 + b31		a32 + b32	a33	+ b33

	a11 b11	+ a12 b21 + a13 b31	a11 b12 + a12 b22 + a13 b32	a11 b13	+ a12 b23	+ a13 b33
AB =	a21 b11	+ a22 b21 + a23 b31	a21 b12 + a22 b22 + a23 b32	a21 b13	+ a22 b23	+ a23 b33

	a31 b11	+ a32 b21 + a33 b31	a31 b12 + a32 b22 + a33 b32	a31 b13	+ a32 b23	+ a33 b33

aTerms are implicitly summed over repeated su ces; hence aikbkj equals bSee also Equation (2.85).

cOr “Hermitian conjugate matrix.” The term “adjoint” is used in quantum physics for the transpose conjugate of a matrix and in linear algebra for the transpose matrix of its cofactors. These deﬁnitions are not compatible, but both are widely used [cf. Equation (2.80)].

dHermitian matrices must also be square (see next table).

2.2 Vectors and matrices	25

Square matricesa

trA = aii

(2.74)

square matrix

Trace

aij

matrix elements

tr(AB) = tr(BA)

(2.75)

aii

implicitly = i aii

detA = ijk...a1ia2j a3k ...

(2.76)

trace

Determinant

= (

−

1)i+1ai1Mi1

(2.77)

det

determinant (or |A|)

(2.78)

Mij

minor of element aij

= ai1Ci1

Cij

cofactor of the

det(AB...N) = detAdetB...detN

(2.79)

element aij

adj

adjoint (sometimes

Adjoint matrix

= Cji

(2.80)

(deﬁnition 2)c

adjA = Cij

written A)

transpose

aij−1 =

Cji

adjA

(2.81)

Inverse matrix

detA

AA−1 = 1

(2.82)

unit matrix

(detA = 0)

(AB...N)−1 = N−1 ...B−1A−1

(2.83)

Orthogonality

aij aik = δjk

(2.84)

δjk

Kronecker delta (= 1

condition

i.e., A˜ = A−1

(2.85)

if i = j, = 0 otherwise)

A is symmetric

(2.86)

Symmetry

A = A,

A is antisymmetric

(2.87)

A = −A,

Unitary matrix

U† = U−1

(2.88)

unitary matrix

†

Hermitian conjugate

examples:

a11

a12

a13

B =

b11

b12

A = a21

a22

a23

b21 b22

a31 a32

a33

trA = a11 + a22 + a33

trB = b11 + b22

detA = a11 a22 a33 − a11 a23 a32 − a21 a12 a33 + a21 a13 a32 + a31 a12 a23 − a31 a13 a22

detB = b11 b22 − b12 b21

a22 a33 − a23 a32

a12 a33 + a13 a32

a12 a23 − a13 a22

A−1 =

a21 a33 + a23 a31

−a11 a33

−

a13 a31

a11 a23 + a13 a21

detA

−a21 a32

−

a22 a31

−

−a11 a22

−

a12 a21

a11 a32 + a12 a31

B−1 =

b22

−b12

detB

−b21

b11

aTerms are implicitly summed over repeated su ces; hence aikbkj equals

k aikbkj .

ijk... is deﬁned as the natural extension of Equation (2.443) to

dimensions (see page 50). M

is the determinant

ij = (−1)

i+j

of the matrix

with the ith row and the jth column deleted. The cofactor C

ij .

Or “adjugate matrix.” See the footnote to Equation (2.71) for a discussion of the term “adjoint.”

26 Mathematics

Commutators

Commutator	[A,B] = AB − BA = −[B,A]	(2.89)	[·,·] commutator
deﬁnition	[A,B] = AB − BA = −[B,A]	(2.89)	[·,·] commutator

Adjoint	[A,B]† = [B†,A†]	(2.90)	† adjoint

Distribution	[A + B,C] = [A,C] + [B,C]	(2.91)

Association	[AB,C] = A[B,C] + [A,C]B	(2.92)

Jacobi identity	[A,[B,C]] = [B,[A,C]] − [C,[A,B]]	(2.93)

Pauli matrices

	σ1 = 0	1	σ2 =	0	i		σ	Pauli spin matrices
Pauli matrices	1	0		i	−0		1i	2	×		2 unit matrix
Pauli matrices	1	0		1	0				×
	1	0		1	0			2		= −1
	σ3 = 0	−1	1 = 0		1	(2.94)	i	i		= −1
Anticommuta-	σiσj + σj σi = 2δij 1					(2.95)	δij	Kronecker delta
tion	σiσj + σj σi = 2δij 1					(2.95)	δij	Kronecker delta
tion

Cyclic	σiσj = iσk					(2.96)
Cyclic
permutation	(σi)2 = 1					(2.97)

Rotation matricesa

Rotation

Ri(θ)

matrix for rotation

R1(θ) =

cosθ

sinθ

(2.98)

about the ith axis

about x1

− sinθ

cosθ

rotation angle

Rotation

cosθ

−

sinθ

R2(θ) =

(2.99)

about x2

sinθ

cosθ

Rotation

cosθ sinθ 0

rotation about x3

(θ) =

sinθ cosθ

(2.100)

about x3

−

rotation about x2

rotation about x3

Euler angles

rotation matrix

cosγcosβ cosα

sinγsinα

cosγcosβ sinα+ sinγcosα

cosγsinβ

R(α,β,γ) =

sinγcosβ cosα

−cosγsinα

−

sinγcosβ sinα+ cosγcosα

− sinγsinβ

−

sinβ cos−α

sinβ sinα

cosβ

(2.101)

aAngles are in the right-handed sense for rotation of axes, or the left-handed sense for rotation of vectors. i.e., a vector v is given a right-handed rotation of θ about the x3-axis using R3(−θ)v → v . Conventionally, x1 ≡ x, x2 ≡ y, and x3 ≡ z.

<<< < Предыдущая 1 2 3 4 56 / 356 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>