
- •Contents
- •Preface
- •How to use this book
- •Chapter 1 Units, constants, and conversions
- •1.1 Introduction
- •1.2 SI units
- •1.3 Physical constants
- •1.4 Converting between units
- •1.5 Dimensions
- •1.6 Miscellaneous
- •Chapter 2 Mathematics
- •2.1 Notation
- •2.2 Vectors and matrices
- •2.3 Series, summations, and progressions
- •2.5 Trigonometric and hyperbolic formulas
- •2.6 Mensuration
- •2.8 Integration
- •2.9 Special functions and polynomials
- •2.12 Laplace transforms
- •2.13 Probability and statistics
- •2.14 Numerical methods
- •Chapter 3 Dynamics and mechanics
- •3.1 Introduction
- •3.3 Gravitation
- •3.5 Rigid body dynamics
- •3.7 Generalised dynamics
- •3.8 Elasticity
- •Chapter 4 Quantum physics
- •4.1 Introduction
- •4.3 Wave mechanics
- •4.4 Hydrogenic atoms
- •4.5 Angular momentum
- •4.6 Perturbation theory
- •4.7 High energy and nuclear physics
- •Chapter 5 Thermodynamics
- •5.1 Introduction
- •5.2 Classical thermodynamics
- •5.3 Gas laws
- •5.5 Statistical thermodynamics
- •5.7 Radiation processes
- •Chapter 6 Solid state physics
- •6.1 Introduction
- •6.2 Periodic table
- •6.4 Lattice dynamics
- •6.5 Electrons in solids
- •Chapter 7 Electromagnetism
- •7.1 Introduction
- •7.4 Fields associated with media
- •7.5 Force, torque, and energy
- •7.6 LCR circuits
- •7.7 Transmission lines and waveguides
- •7.8 Waves in and out of media
- •7.9 Plasma physics
- •Chapter 8 Optics
- •8.1 Introduction
- •8.5 Geometrical optics
- •8.6 Polarisation
- •8.7 Coherence (scalar theory)
- •8.8 Line radiation
- •Chapter 9 Astrophysics
- •9.1 Introduction
- •9.3 Coordinate transformations (astronomical)
- •9.4 Observational astrophysics
- •9.5 Stellar evolution
- •9.6 Cosmology
- •Index

2.3 Series, summations, and progressions |
27 |
|
|
2.3Series, summations, and progressions
Progressions and summations
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
Sn = a+ (a+ d) + (a+ 2d) + · · · |
|
|
|
|
|
|
|
n |
|
number of terms |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
+ [a+ (n− 1)d] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.102) |
Sn |
|
sum of n successive |
|
|||||||||||||||||||||||||
Arithmetic |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
terms |
|
|||||||||||||||||||||||||||
progression |
= |
n |
[2a+ (n− 1)d] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.103) |
a |
|
first term |
|
||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
common di erence |
|
||
|
= |
|
(a+ l) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.104) |
l |
|
last term |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Sn = a+ ar + ar2 + |
· · · |
+ arn−1 |
|
|
|
|
|
|
|
(2.105) |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Geometric |
= a |
|
1 − rn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.106) |
r |
|
common ratio |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
progression |
|
|
|
|
|
|
|
|
1 |
− |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
S∞ = |
|
|
|
|
a |
|
|
|
(|r| < 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.107) |
|
|
|
|
||||||||||||||||||||||
|
1 − r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Arithmetic |
|
|
|
|
|
|
|
|
1 |
|
(x1 + x2 + · · · + xn) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
mean |
x a = |
|
|
|
|
|
|
|
|
|
|
|
|
(2.108) |
. |
a |
arithmetic mean |
|
||||||||||||||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
Geometric |
x g = (x1x2x3 ...xn) |
1/n |
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.109) |
. |
|
geometric mean |
|
||||||||||||||||||||||||||||||||
mean |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x h = n |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
− |
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Harmonic mean |
|
|
|
|
+ |
|
+ · · · + |
|
|
|
|
|
|
|
(2.110) |
. |
h |
harmonic mean |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
x1 |
x2 |
|
xn |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
Relative mean |
x a ≥ x g ≥ x h |
|
|
|
if xi > 0 for all i |
(2.111) |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
magnitudes |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i = |
n |
(n+ 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.112) |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
i=1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i2 = |
n |
(n+ 1)(2n+ 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.113) |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
i=1 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i3 = |
n2 |
(n+ 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.114) |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Summation |
|
4 |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+ 3n− 1) |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
formulas |
|
i |
= |
|
(n+ 1)(2n+ 1)(3n |
(2.115) |
i |
|
dummy integer |
|
||||||||||||||||||||||||||||||||||||||||||
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
∞ |
(−1)i+1 |
= 1 |
− |
|
|
|
+ |
|
|
|
− |
|
|
|
+ ... = ln2 |
(2.116) |
|
|
|
|
|||||||||||||||||||||||||||||||
|
i=1 |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
∞ |
|
(−1)i+1 |
= 1 |
− |
1 |
|
+ |
1 |
|
− |
1 |
|
+ ... = |
π |
|
(2.117) |
|
|
|
|
|||||||||||||||||||||||||||||||
|
i=1 2i |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
3 5 |
|
7 |
|
|
|
π2 |
4 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
∞ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
= 1 + |
|
|
|
+ |
|
+ |
|
|
|
+ ... = |
|
|
|
|
|
|
(2.118) |
|
|
|
|
||||||||||||||||||||||||||
|
i=1 |
|
i2 |
|
4 |
9 |
16 |
6 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Euler’s |
γ |
|
lim |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
+ |
|
|
|
+ |
1 |
|
|
lnn |
|
|
(2.119) |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
γ |
|
Euler’s constant |
|
||||||||||||||||||||||||
constanta |
= n→∞ 1 + 2 |
|
|
3 |
|
|
|
· · · |
|
|
|
n − |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
aγ 0.577215664...

28 Mathematics
Power series
Binomial |
(1 + x)n = 1 + nx+ |
n(n− 1) |
x2 |
+ |
n(n− 1)(n− 2) |
x3 |
+ |
· · · |
|
|
(2.120) |
|||||||||||||||||||||||||||||
seriesa |
|
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Binomial |
n |
|
n |
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Cr ≡ r ≡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.121) |
|||
coe cientb |
|
r!(n− r)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Binomial |
|
n |
|
n |
|
|
|
n |
k |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
theorem |
(a+ b) |
= k=0 |
k a − b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.122) |
|||||||||
Taylor series |
|
|
|
|
|
|
|
|
(1) |
|
|
|
|
|
|
x2 |
|
(2) |
|
|
|
|
|
|
|
xn−1 |
|
|
|
(n |
1) |
|
|
|||||||
(about a)c |
f(a+ x) = f(a) + xf |
|
(a) + |
|
|
f |
|
|
(a) + · · · + |
|
|
|
|
f |
|
− |
|
(a) + · · · |
(2.123) |
|||||||||||||||||||||
|
2! |
|
|
(n |
− |
1)! |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Taylor series |
f(a + x) = f(a) + (x |
|
)f |
a + |
(x · )2 |
f |
a + |
(x · )3 |
f |
a |
+ |
· · · |
|
(2.124) |
||||||||||||||||||||||||||
(3-D) |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
· |
| |
|
|
|
|
|
2! |
| |
|
|
|
3! |
|
|
|
| |
|
|
|
|
|
|
||||||||||
Maclaurin |
|
|
|
|
(1) |
|
|
|
|
|
x2 |
(2) |
|
|
|
|
|
|
|
xn−1 |
|
|
|
(n |
|
1) |
|
|
|
|
||||||||||
series |
f(x) = f(0) + xf |
|
|
(0) + |
|
f |
|
|
(0) + · · · |
+ |
|
|
|
|
f |
|
− |
|
|
(0) + · · · |
(2.125) |
|||||||||||||||||||
|
|
2! |
|
|
(n |
− |
1)! |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
aIf n is a positive integer the series terminates and is valid for all x. Otherwise the (infinite) series is convergent for
|x| < 1.
bThe coe cient of xr in the binomial series.
cxf(n)(a) is x times the nth derivative of the function f(x) with respect to x evaluated at a, taken as well behaved around a. (x · )nf|a is its extension to three dimensions.
Limits
ncxn → 0 |
as |
n → ∞ |
if |x| < 1 (for any fixed c) |
|
(2.126) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
xn/n! → 0 as |
n → ∞ (for any fixed x) |
|
|
|
|
(2.127) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(1 + x/n)n → ex |
as |
n → ∞ |
|
|
|
|
|
|
|
(2.128) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
xlnx → 0 |
as x → 0 |
|
|
|
|
|
|
|
|
|
(2.129) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sinx |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
→ 1 |
as |
x → 0 |
|
|
|
|
|
|
|
|
|
(2.130) |
|
x |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
∞ |
|
f(x) |
= |
f(1)(a) |
(l’Hopital’sˆ rule) |
(2.131) |
|||
If |
f(a) = g(a) = 0 or |
then |
lim |
|
|
|
|
||||||||
|
g(1)(a) |
||||||||||||||
|
|
|
|
|
|
|
x→a g(x) |
|
|
|
|||||

2.3 Series, summations, and progressions |
29 |
|
|
Series expansions
exp(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(for all x) |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 + x+ 2! + 3! + · · · |
|
|
|
|
|
|
|
|
|
|
(2.132) |
2 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
ln(1 + x) |
|
|
|
|
|
|
|
x2 |
|
|
|
x3 |
|
|
|
|
x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x− |
|
|
|
|
|
+ |
|
|
|
|
− |
|
|
+ · · · |
|
|
|
|
|
|
|
|
|
(2.133) |
(−1 < x ≤ 1) |
|
|
||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
3 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
ln |
1 + x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
x5 |
|
|
|
|
|
x7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
x+ |
|
+ |
|
|
|
|
+ |
|
|
|
|
|
+ · · · |
|
|
(2.134) |
(|x| < 1) |
|
|||||||||||||||||||||||||||||||||
1 − x |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
5 |
7 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
cos(x) |
|
|
|
|
|
|
|
x2 |
|
|
|
|
x4 |
|
|
|
|
|
x6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(for all x) |
|
|
|||||||||||
|
1 − 2! + |
4! − |
6! + · · · |
|
|
|
|
|
|
|
|
|
(2.135) |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
sin(x) |
|
|
|
|
|
|
|
x3 |
|
|
|
x5 |
|
|
|
|
|
x7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(for all x) |
|
|
||||||||||||
|
x− 3! + |
5! − |
7! + · · · |
|
|
|
|
|
|
|
|
|
(2.136) |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
tan(x) |
|
|
|
|
|
|
|
x3 |
|
|
|
2x5 |
|
|
17x7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
x+ |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
· · · |
|
|
|
|
|
|
(2.137) |
(|x| < π/2) |
|
|||||||||||||||||||||
|
3 |
|
|
15 |
|
|
|
315 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
sec(x) |
|
|
|
|
|
|
|
x2 |
|
|
|
5x4 |
|
61x6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
1 + |
|
|
|
|
+ |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
+ · · · |
|
|
|
(2.138) |
(|x| < π/2) |
|
|||||||||||||||||||||||||||
|
2 |
|
|
24 |
|
|
720 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
csc(x) |
|
1 |
|
|
|
x |
|
|
|
7x3 |
|
|
31x5 |
|
+ · · · |
|
|
|
(|x| < π) |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
(2.139) |
|
|||||||||||||||||||||||||||
|
|
x |
6 |
|
|
360 |
15120 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
cot(x) |
|
1 |
|
|
|
x |
|
|
|
x3 |
|
|
|
|
2x5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
− |
|
|
|
|
|
− |
|
|
|
|
− |
|
|
|
− · · · |
|
|
|
|
|
|
(2.140) |
(|x| < π) |
|
||||||||||||||||||||||||||
|
|
x |
3 |
|
|
45 |
945 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
arcsin(x)a |
x+ |
1 |
|
|
x3 |
+ |
|
1 · 3 |
x5 |
+ |
|
|
1 · 3 · 5 |
|
x7 |
|
(2.141) |
( x |
< 1) |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 3 2 |
· |
4 5 2 |
· |
4 |
· |
6 7 · · · |
|
| | |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
x5 |
|
|
|
x7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
x− |
|
|
|
|
|
+ |
|
− |
|
|
|
+ · · · |
|
|
|
|
|
|
(|x| ≤ 1) |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
5 |
|
7 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
π |
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
arctan(x) |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.142) |
(x > 1) |
|
|
|||||||||||||||||||
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
· · · |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
2 |
|
x |
|
|
|
3x |
|
|
5x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
π |
|
|
|
1 + 13 |
|
|
|
|
|
|
|
15 + |
|
|
|
|
(x < −1) |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
− |
2 |
− |
x |
|
3x |
− |
5x |
|
|
|
|
· · · |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
x |
4 |
|
|
|
|
|
x |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
cosh(x) |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(for all x) |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 + 2! + |
4! + |
6! + · · · |
|
|
|
|
|
|
|
|
|
(2.143) |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
sinh(x) |
|
|
|
|
|
|
|
x3 |
|
|
|
x5 |
|
|
|
|
|
x7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(for all x) |
|
|
||||||||||||
|
x+ 3! + |
5! + |
7! + · · · |
|
|
|
|
|
|
|
|
|
(2.144) |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
tanh(x) |
|
|
|
|
|
|
|
x3 |
|
|
|
2x5 |
|
|
17x7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
x− |
|
+ |
|
− |
|
|
+ · · · |
|
|
|
(2.145) |
(|x| < π/2) |
|
||||||||||||||||||||||||||||||||||||||||
|
3 |
15 |
|
315 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
aarccos(x) = π/2 − arcsin(x). Note that arcsin(x) ≡ sin−1(x) etc. barccot(x) = π/2 − arctan(x).

30 Mathematics
Inequalities
Triangle |
|a1| − |a2| ≤ |a1 + a2| ≤ |a1| + |a2| ; |
|
|
(2.146) |
|||||||||||
inequality |
|
|
|
|
|ai| |
|
|
|
|
|
|
(2.147) |
|||
n |
ai |
≤ |
n |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
if |
a1 |
|
a2 |
≥ |
a3 |
≥ |
... |
≥ |
an |
|
|
(2.148) |
||
|
|
|
|
≥ |
|
|
|
|
|
|
|
|
|||
Chebyshev |
and |
|
|
b1 ≥ b2 ≥ b3 |
≥ ... ≥ bn |
bi |
|
(2.149) |
|||||||
inequality |
then |
|
n |
n |
aibi ≥ |
n |
|
ai n |
|
(2.150) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
i=1 |
|
|
|
i=1 |
i=1 |
|
|
|
||
|
n |
|
|
|
2 |
|
n |
|
n |
|
|
|
|
||
Cauchy |
|
|
|
|
|
|
|
|
|
||||||
inequality |
|
|
aibi ≤ |
|
ai2 |
|
bi2 |
|
|
(2.151) |
|||||
|
i=1 |
|
|
|
|
i=1 |
|
i=1 |
|
|
|
||||
inequality |
a |
f(x)g(x) dx |
≤ a |
[f(x)]2 dx a |
[g(x)]2 dx |
(2.152) |
|||||||||
Schwarz |
b |
|
|
|
|
|
|
2 |
|
|
b |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.4 Complex variables Complex numbers
|
|
|
|
|
|
|
z |
|
complex variable |
|||
Cartesian form |
z = x+ iy |
(2.153) |
i |
|
i |
2 |
= −1 |
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
x,y |
real variables |
||||
|
|
|
|
|
r |
|
amplitude (real) |
|||||
Polar form |
z = reiθ = r(cosθ + isinθ) |
(2.154) |
|
|||||||||
|
|
|
|
|
|
|
θ |
|
phase (real) |
|||
|
|
|
|
|
|
|
|
|||||
Modulusa |
|z| = r = (x2 + y2)1/2 |
(2.155) |
z |
| |
modulus of z |
|||||||
|
|z1 · z2| = |z1| · |z2| |
(2.156) |
| |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
|
θ = argz = arctan |
y |
|
(2.157) |
|
|
|
|
|
|||
Argument |
x |
argz |
argument of z |
|||||||||
|
|
|
|
|||||||||
arg(z1z2) = argz1 + argz2 |
(2.158) |
|||||||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
Complex |
z = x |
− |
iy = re−iθ |
(2.159) |
z |
|
|
|
||||
arg(z ) = − argz |
(2.160) |
complex conjugate of |
||||||||||
conjugate |
|
|
z = reiθ |
|||||||||
|
z · z = |z|2 |
(2.161) |
|
|
|
|
|
|||||
Logarithmb |
lnz = lnr + i(θ + 2πn) |
(2.162) |
n |
|
integer |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
aOr “magnitude.”
bThe principal value of lnz is given by n = 0 and −π < θ ≤ π.
2.4 Complex variables |
31 |
|
|
Complex analysisa
|
|
if |
f(z) = u(x,y) + iv(x,y) |
|
|
||||||||||||||||
Cauchy– |
|
then |
|
∂u |
= |
∂v |
|
|
|
|
|
|
|
|
(2.163) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Riemann |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
∂x |
|
∂y |
|
|
|
|
|
|
||||||||||
equationsb |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
∂u |
|
|
|
|
|
|
∂v |
|
|
|
|
|
|
||||||
|
|
|
|
= − |
|
|
|
|
|
(2.164) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
∂y |
∂x |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cauchy– |
|
c f(z) dz = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Goursat |
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.165) |
|||||||
theoremc |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Cauchy |
|
f(z0) = |
1 |
|
|
|
|
f(z) |
|
dz |
|
(2.166) |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
integral |
|
|
|
2πi c z − z0 |
|
|
|||||||||||||||
formulad |
|
f(n)(z0) = |
n! |
|
c |
|
|
f(z) |
|
|
|||||||||||
|
|
|
|
|
|
dz |
|
(2.167) |
|||||||||||||
|
2πi |
(z − z0)n+1 |
|
||||||||||||||||||
|
|
f(z) = |
|
|
∞ |
|
an(z − z0)n |
|
(2.168) |
||||||||||||
Laurent |
e |
|
|
|
|
|
|||||||||||||||
|
|
n=−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
expansion |
|
|
|
|
|
|
1 |
|
|
c |
f(z ) |
dz |
|
||||||||
|
|
where |
|
|
an = |
|
|
(2.169) |
|||||||||||||
|
|
|
|
2πi |
(z − z0)n+1 |
||||||||||||||||
Residue |
|
c f(z) dz = 2πi enclosed residues |
(2.170) |
||||||||||||||||||
theorem |
|
||||||||||||||||||||
z |
complex variable |
|
i |
i2 = −1 |
2 |
x,y |
real variables |
|
f(z) |
function of z |
|
u,v |
real functions |
|
(n) |
nth derivative |
|
|
an |
Laurent coe cients |
a−1 |
residue of f(z) at z0 |
z |
dummy variable |
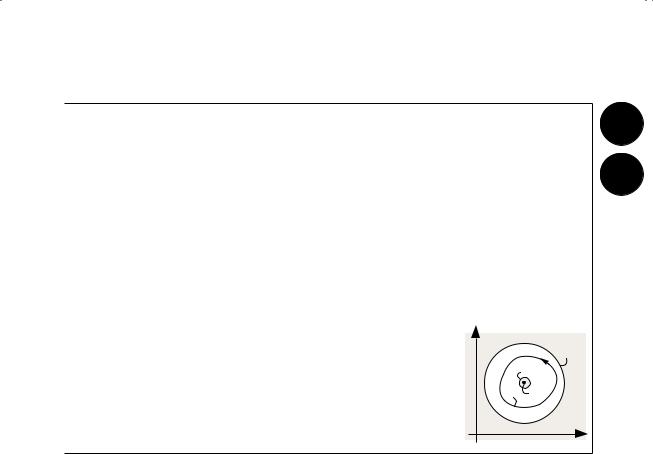
y
c2
c1
cz0
x
aClosed contour integrals are taken in the counterclockwise sense, once. bNecessary condition for f(z) to be analytic at a given point.
cIf f(z) is analytic within and on a simple closed curve c. Sometimes called “Cauchy’s theorem.” dIf f(z) is analytic within and on a simple closed curve c, encircling z0.
eOf f(z), (analytic) in the annular region between concentric circles, c1 and c2, centred on z0. c is any closed curve in this region encircling z0.
