
- •Оглавление
- •Аннотация
- •Задачи курса
- •§1. Множества, действия над множествами
- •1.1. Общие свойства множеств
- •1.2. Натуральные числа
- •1.2. Целые числа
- •1.3. Рациональные числа
- •1.4. Иррациональные числа
- •1.5. Действительные числа
- •1.6. Модуль действительного числа
- •1.7. Подмножества множества R
- •1.8. Свойства множества R
- •§2. Функции действительного переменного
- •2.1. Способы задания функции
- •2.2. Элементарные свойства функций
- •Свойства возрастающих и убывающих функций
- •2.3. Элементарные функции
- •§3. Числовая последовательность. Предел числовой последовательности
- •3.1. Расширенная числовая прямая. Окрестности точек расширенной числовой прямой
- •3.2. Определение числовой последовательности и ее предела
- •3.3. Основные свойства предела последовательности
- •3.4. Бесконечно малые последовательности и их свойства
- •3.5. Арифметические действия над пределами последовательностей
- •3.6. Вычисление пределов последовательностей
- •§4. Предел функции
- •4.1. Определения предела функции
- •4.2. Свойства пределов функций
- •4.3. Замечательные пределы.
- •4.5. Односторонние пределы
- •§5. Непрерывность функции
- •5.1. Определение непрерывности функции в точке
- •5.2. Точки разрыва функции и их классификация
- •5.3. Свойства функций, непрерывных на отрезке.
- •§6. Производная функции одной переменной
- •6.1. Определение производной функции в точке
- •6.3. Правила вычисления производной. Таблица производных
- •6.4. Таблица производных
- •6.5. Физический и геометрический смысл производной
- •6.7. Дифференцируемость функции в точке. Дифференциал.
- •6.8. Производные высших порядков
- •6.9. Производная функции, заданной параметрически
- •6.10. Производная функции, заданной неявно
- •6.11. Дифференциалы высших порядков
- •§7. Основные теоремы дифференциального исчисления. Формула Тейлора
- •7.1. Основные теоремы дифференциального исчисления
- •7.2. Правила Лопиталя
- •7.3. Формулы Тейлора и Маклорена для многочлена
- •7.4. Формулы Тейлора и Маклорена для произвольной функции
- •7.5. Разложение по формуле Тейлора (Маклорена) некоторых элементарных функций
- •7.6. Приложения формулы Тейлора
- •§8. Исследование функций с помощью производной
- •8.1. Условия постоянства функции на промежутке
- •8.2. Условия монотонности функции на промежутке
- •8.3. Экстремум функции
- •8.4. Выпуклость функции
- •8.5. Точки перегиба
- •8.6. Асимптоты функции
- •8.7. Полное исследование функции и построение её графика
- •Наибольшее и наименьшее значения функции
- •§9. Кривые на плоскости и в пространстве
- •9.1. Понятие кривой
- •9.3. Натуральный параметр
- •9.4. Кривизна кривой и радиус кривизны
- •9.5. Вычисление кривизны плоской кривой
- •9.6. Центр и круг кривизны. Эволюта и эвольвента
- •9.7. Формулы для координат центра кривизны
- •9.8. Эволюта и эвольвента кривой
- •Список литературы
§3. Числовая последовательность. Предел числовой последовательности
3.1. Расширенная числовая прямая. Окрестности точек расширенной числовой прямой
|
|
|
Расширенная |
числовая прямая |
|
– это |
множество R действительных чисел, к |
|||||||
|
|
|
R |
|||||||||||
которым добавляются символы бесконечности + ∞ |
, − ∞ и ∞ : |
|||||||||||||
|
|
|
|
|
|
|
|
|
= R {+ ∞ ,− ∞ ,∞ }. |
|||||
|
|
|
|
|
|
|
|
R |
||||||
|
|
|
Символ ∞ означает + ∞ или − ∞ . |
|
|
|
|
|||||||
|
|
|
Действия с символом бесконечности определяются следующим образом (здесь C — |
|||||||||||
любое действительное число): |
|
|
|
|
|
|||||||||
|
|
∞ + C = ∞ , (+ ∞ ) + (+ ∞ ) = + ∞ , (− ∞ ) + (− ∞ ) = − ∞ ; |
||||||||||||
|
|
¥ |
× C = ¥ |
(при C ¹ 0), ¥ × ¥ = ¥ ; |
|
|
|
|
|
|||||
|
|
(+ ¥ )+ ∞ = + ¥ , (+ ¥ )− ∞ = 0; |
|
|
|
|
|
|||||||
|
|
C |
= 0, |
C = ¥ , |
|
0 |
= 0 (при C ¹ 0). |
|
|
|
|
|
||
|
|
¥ |
|
|
|
|
|
|
|
|||||
|
|
|
0 |
|
C |
|
|
|
|
|
||||
Не определены следующие действия: |
|
|
|
|
|
|||||||||
∞ |
|
0 |
|
|
), (+ ¥ ) - (+ ¥ ),1∞ , ¥ |
0 |
|
|
0 |
|
||||
¥ |
, |
0 , 0× ¥ , (+ ¥ ) + (- ¥ |
|
, 0 |
- неопределенности. |
|||||||||
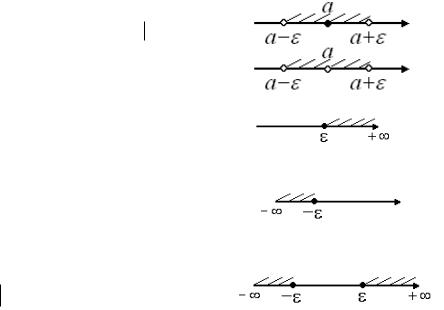
Понятие ε-окрестности точки а расширенной числовой прямой
I.a R
Uε (a) = {x Î R | a - ε < x < a + ε } = {x Î R | x - a |< ε }
U˚ a ={x R 0 x−a } - выколотая окрестность (ε – маленькое).
II.a = + ∞
Uε (+ ∞ ) = {x R | x > ε }
(ε – большое).
III.a = − ∞
Uε (− ∞ ) = {x R | x < − ε }
(ε – большое).
IV. a = ∞
Uε (∞ ) = {x R | x |> ε }
(ε – большое).
3.2. Определение числовой последовательности и ее предела
Определение. Числовая последовательность – это функция натурального аргумента, принимающая действительные (или комплексные) значения. При этом каждому натуральному числу по некоторому правилу сопоставляется действительное (или
комплексное) число: f : N → R , n ǀ® f(n) = f n.
20

Последовательностью называют также множество значений этой функции. Обычно ее записывают в виде { fn}n N или { f1, f2 ,..., fn ,...} , где f1 – первый член последовательности, f2 –
второй член последовательности, fn – общий (n-й) член последовательности.
xn = |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
n + 1 |
|
|
|
|
|
|
|
|
|
|
|
||
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
||
1 , x |
|
= 2 |
|
|
|
= 3 |
|
|
|
= 4 |
|
|||
x = |
2 |
, |
x |
3 |
, |
x |
4 |
, ... |
||||||
1 |
2 |
|
3 |
|
|
4 |
|
|
5 |
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
Определение. Предел числовой последовательности {xn}n N - это точка a расширенной
числовой прямой, такая что для любой её окрестности все члены последовательности, начиная с некоторого, попадают в эту окрестность.
Запись на языке символов: ε > |
0 n0 = n0 (ε ) N : n > n0 xn Uε (a) . |
|
Обозначение предела: |
lim xn=a |
или xn®a (n®¥). |
n ∞ |
||
Поскольку а – это либо число, либо одна из бесконечностей, определение предела можно уточнить, рассмотрев следующие 4 случая.
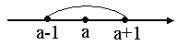
1 случай. a – число ( a R ).
lim xn = a ε > 0 n0 = n0 (ε ) N : n > n0 | xn − a |< ε .
n→ + ∞
Когда предел последовательности конечен, для любого ε > 0 внутрь интервала (a - ε, a + ε) попадут все члены последовательности, начиная с некоторого номера n0+1. Вне этого интервала может находиться только конечное число членов последовательности (не более n0). С уменьшением ε номер n0 может увеличиваться.
Пример. xn = |
|
n |
|
, |
|
lim |
xn = 1. |
|
|
|
|||||||
n + |
1 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
n→ + ∞ |
|
|
|
|
|
|
||||
ε > 0 n0 = n0 (ε ) N : n > n0 |
| xn − 1|< ε |
|
|||||||||||||||
Зафиксируем e и найдем n0: |
|
|
|
|
|
|
|||||||||||
|
n |
|
- 1 |
|
< e |
|
- |
1 |
|
< e |
|
1 |
|
< e |
1 |
< n + 1 |
|
|
|
|
|
|
|||||||||||||
|
n + |
1 |
n + |
1 |
|
n + 1 |
e |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
Если e = 0,01 , то n0 = 99; если e = 0,001 , то n0 = 999
n > |
1 |
- 1 |
n0 = |
é |
1 |
ù |
e |
ê |
e |
- 1ú . |
|||
|
|
|
ë |
û |
и так далее.
2 случай. |
a = + ∞ . |
lim xn = + ∞ |
ε > 0 n0 = n0 (ε ) N : n > n0 xn > ε . |
n→ + ∞ |
|
Пример. xn = 2n + 5.
3 случай. |
a = − ∞ . |
lim xn = − ∞ |
ε > 0 n0 = n0 (ε ) N : n > n0 xn < − ε . |
n→ + ∞ |
|
Пример. xn = -n2.
4 случай. |
a = |
∞ . |
lim xn = ∞ |
ε |
> 0 n0 = n0 (ε ) N : n > n0 | xn |> ε . |
n→ + ∞ |
|
|
Пример. xn = (-1)n×n.
Не каждая последовательность имеет предел:
Пример последовательности, не имеющей ни конечного, ни бесконечного предела: xn = (- 1)n .
21
Определения.
1). Последовательность сходится, если у нее существует конечный предел (число).
2). Последовательность называется бесконечно большой, если ее предел равен бесконечности (с любым знаком: + ∞ , − ∞ или ∞ ).
3). Последовательность называется бесконечно малой, если ее предел равен нулю.
4). Последовательность возрастает, если "nÎN an+1>an (или an+1/an > 1 для положительной последовательности).
5). Последовательность убывает, если "nÎN an+1<an (или an+1/an < 1 для положительной последовательности).
6). Последовательность ограничена сверху, если существует MÎR, такое что "nÎN an £
M.
7). Последовательность ограничена снизу, если существует mÎR, такое что "nÎN an ³ m. 8). Последовательность ограниченна, если она ограничена и сверху и снизу (то есть
существуют m, M Î R, такие что "nÎN m £ an £ M.
3.3. Основные свойства предела последовательности
Теорема 1. Если последовательность сходится, то ее предел единственный. Доказательство (методом от противного).
Пусть lim xn = a , lim xn = b , и предположим, что a ¹ b. Зафиксируем e |
= |
| b − a | |
> 0 . |
||||||||||||||||||
n→ + ∞ |
n→ + ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| b − a | |
2 |
|
|||
По определению предела |
lim xn = a |
: |
$ n Î |
N : |
" n > |
n |
| x |
n |
- a |< |
. (*) |
|
||||||||||
|
|
|
|
||||||||||||||||||
n→ + ∞ |
|
1 |
|
|
|
|
1 |
|
|
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Аналогично, поскольку lim xn = b , то $ n2 Î |
N : |
" n > |
|
n2 |
| xn - b |< |
|
| b − |
a | |
. (**) |
|
|||||||||||
2 |
|
|
|||||||||||||||||||
|
n→ + ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда при |
n > max{n1, n2} верны |
оба |
неравенства (*) |
и (**). Поэтому |
при таких n |
||||||||||||||||
выполняются соотношения: |
|
|
|
|
| b − a | |
|
|
| b − a | |
|
|
|
|
|
|
|
|
|||||
| b - a |= | b - xn + xn - a |£ | b - xn | + | xn - a |< |
+ |
|
= | b - a |. |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
Получили противоречие: |b-a| < |b-a|. Значит предположение a¹b не верно, и двух разных пределов у последовательности быть не может. ¨
Теорема 2. |
Если |
последовательность сходится, |
то |
|
она ограничена (то есть если |
||||
lim xn = |
a R , то m R, M |
R : |
n N m ≤ |
x |
n |
≤ M ). |
|||
n→ + ∞ |
|
|
|
|
|
|
|
|
|
Доказательство. Пусть ε |
= 1 . Тогда, по определению предела, |
||||||||
$ n0 Î N : " n > n0 |
a - 1 < |
xn < a + 1, то |
есть, |
начиная |
с |
номера n0+1, все члены |
|||
последовательности ограничены числами a-1 и a+1. Вне |
|||||||||
окрестности |
(a-1, a+1) |
могут находиться |
только элементы |
||||||
x1 , x2 , ..., xn0 . |
|
|
|
|
|
|
|
|
|
Положим |
M = max{a + 1, x1 , x2 , ..., xn0 } , |
m = |
min{a - 1, x1 , x2 , ..., xn0 }. Тогда n N |
||||||
выполнены неравенства xn £ M и xn ³ m. Таким образом, последовательность ограничена и сверху и снизу. ■
Обратное утверждение (если последовательность ограничена, то она сходится) не верно: Пример ограниченной последовательности, не имеющей предела: xn = (- 1)n .
Хотя при всех nÎN -1£xn£1, но lim xn не существует.
n→ + ∞
22
Определение. Подпоследовательностью последовательности {xn} называется последовательность xn1 , xn2 ,...xnk ,... , где n1<n2<…<nk<… .
Несмотря на то, что ограниченная последовательность не всегда сходится, верна следующая теорема:
Теорема 3 (Больцано-Вейерштрасса). Из любой ограниченной последовательности можно выбрать сходящуюся подпоследовательность.
Без доказательства.
Пример. |
Ограниченная |
последовательность |
xn = (− 1)n |
имеет |
сходящиеся |
подпоследовательности x2n = 1 (сходится к 1) и x2n-1 = −1 (сходится к −1). |
|
||||
Определение.
1)Частичный предел последовательности – предел любой из ее подпоследовательностей.
2)Верхний предел последовательности {xn} – это наибольший из всех ее частичных
пределов. Он обозначается lim xn . n→ + ∞
3) Нижний предел последовательности {xn} – это наименьший из всех ее частичных
пределов. Обозначается |
|
lim xn . |
|||
|
|
|
|
n→ + ∞ |
|
|
|
|
(− 1)n = 1 |
, lim (− 1)n = − 1. |
|
Пример. |
lim |
||||
|
n→ + ∞ |
|
n→ + ∞ |
||
Теорема 4. (Критерий Коши сходимости последовательности.)
Последовательность сходится тогда и только тогда, когда выполняется условие Коши
ε > 0 n0 = n0 (ε ) N : n > n0 , m > n0 | xn − xm |< ε
(т.е. далекие члены последовательности близки между собой).
Без доказательства.
Теорема 5. (О существовании предела монотонной ограниченной последовательности.)
Любая неубывающая и ограниченная сверху последовательность сходится к своей точной
верхней грани (то есть если { |
xn |
} |
и ограничена сверху, то |
|
lim |
xn |
= sup xn |
R |
). |
|
|
n→ + ∞ |
|
n N |
|
Доказательство. Так как по свойству 1 множества действительных чисел любое непустое ограниченное сверху подмножество R имеет точную верхнюю грань, то существует
sup xn = ξ R . Покажем, что ξ и есть предел последовательности { xn }. |
||||
n N |
|
|
|
|
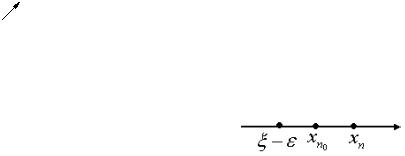
По определению sup имеем: |
|
|
|
|
n N xn ≤ ξ , ε > 0 n0 : xn > ξ − ε . |
|
|
|
|
0 |
|
|
|
|
А так как { xn } – неубывающая, то n > n0 xn > |
xn > |
ξ − |
ε . |
|
|
0 |
|
|
|
Поэтому при любом n > n0 выполнено ξ−ε < xn < ξ. |
n > |
n0 |
| xn − ξ |< ε . |
|
Значит по любому ε > 0 нашли номер n0, такой что |
||||
lim xn = ξ |
. ■ |
|
||
По определению предела это означает, что n→ + ∞ |
|
|
||
Ниже мы применим эту теорему для доказательства существования числа е.
Теорема 6. (О предельных переходах в неравенствах.)
Пусть n N x |
n |
≤ y |
n |
, и |
lim xn = a , |
lim yn = b . Тогда a ≤ b . |
|
|
|
n→ + ∞ |
n→ + ∞ |
23
Доказательство (методом от противного).
Допустим, что a > b. По определению предела последовательности для ε |
= a − |
b > 0 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a − b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
$ n1 Î |
N : |
|
" n > |
n1 |
|
|
| xn - a |< |
, |
|
|
|
|
|
|
|
(*) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
$ n2 Î |
N : |
|
" n > |
n2 |
|
| yn - b |< |
a − b . |
|
|
|
|
|
|
|
(**) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n > max{n1, n2} |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
таких n |
|||||||||||||||
Тогда |
|
при |
|
верны |
оба |
неравенства |
(*) и |
(**). Поэтому |
при |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
выполняются соотношения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a − b |
+ a − b = a - b . |
|
|
||||||||||||||||||||||||||||||||||||||||
a - b = a - xn + xn - b £ a - xn + yn - b £ | a - xn | + | yn - b |< |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Получили противоречие: a−b < a−b. Значит допущение a > b не верно, и a ≤ b . ■ |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Нужно обратить внимание на то, что при переходе к пределу в неравенствах строгое |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
неравенство может перейти в нестрогое. Например, |
1 |
< |
|
|
2 |
|
, но |
lim |
1 |
|
= |
|
lim |
2 . |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
n |
|
|
n |
n |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n→ ∞ |
|
|
|
n→ ∞ |
n |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Число е определяется как предел последовательности xn |
= |
æ |
|
1 ö |
n |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
ç 1+ |
|
÷ |
: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
n ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение. |
|
|
|
|
|
|
|
|
|
|
|
|
e = |
lim |
æ |
1+ |
1 |
ö n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
n |
÷ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n→ ∞ |
è |
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Число е в математике играет особую роль. Оно, в частности, является основанием |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
натуральных логарифмов. Число е – иррационально, а значит |
|
|
представимо |
в виде |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
бесконечной десятичной непериодической дроби: е = 2,718281828459045… |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Докажем существование предела последовательности |
|
|
xn = |
æ |
1+ |
1 ö |
n |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ç |
n |
÷ |
|
|
. Согласно теореме 5, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
ø |
|
|
|
|
|
|
|
|
|
||
достаточно доказать, что последовательность ограничена сверху и возрастает. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1) Ограниченность сверху. Применим бином Ньютона: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
æ |
|
|
|
1 |
ö |
n |
|
|
|
n |
k |
n k æ 1 |
ö |
k |
|
|
|
|
|
|
1 |
|
|
n × (n - 1) 1 n × (n - 1) × (n - 2) 1 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
ç |
1+ |
|
|
|
÷ |
|
= |
|
å |
|
Cn × 1 − |
|
× ç |
|
|
|
÷ = |
1+ |
n × |
|
+ |
|
|
|
|
|
× |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
|
|
|
+ |
...+ |
|
|
|||||||||||||
n |
|
|
|
|
|
n |
n |
|
2! |
|
|
n |
2 |
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
n |
3 |
|
|
|
|||||||||||||||||||||||||||||||||||||
è |
|
|
|
ø |
|
|
|
|
k = 0 |
|
|
|
|
|
|
è |
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поэтому |
||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
× n - 1 + |
|
1 |
|
|
n - 1 |
× n - |
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
(n - 1)! |
|
1 |
|
|
|
|
n! |
|
|
||||||||||||||||||
+ |
|
n × |
|
|
|
+ |
|
1× |
= |
2 + |
|
|
|
|
|
× |
+ ... + |
|
|
|
|
|
|
|
|
× |
+ |
|
× |
|
|
. |
|
|
|
|||||||||||||||||||||||||||||||||||
|
nn− 1 |
|
|
|
nn |
2! |
3! |
|
n |
|
|
|
|
(n - 1)! |
|
n! |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
nn− 2 |
|
|
|
|
nn |
|
|
|
||||||||||||||||||||||||||||||
xn = |
|
|
|
|
1 |
|
æ |
|
|
1 ö |
|
1 |
|
|
æ |
|
|
1 |
ö æ |
|
|
|
2 ö |
|
|
|
|
1 |
|
|
|
|
|
|
æ |
|
1 |
ö |
|
|
|
æ |
|
|
n - 2 |
ö |
|
|
|
|
|
|
|
|||||||||||||||||
2 + |
|
|
× ç |
1- |
÷ |
+ |
|
|
|
|
× |
ç |
1- |
|
|
÷ × |
ç 1- |
|
|
÷ |
+ |
...+ |
|
|
|
|
|
|
|
× |
|
ç 1 |
- |
|
÷ |
× |
...× ç 1 |
- |
|
|
|
|
|
÷ |
+ |
|
|
|
|
|
||||||||||||||||||||
2! |
3! |
|
n |
|
n |
|
(n - 1)! |
|
n |
|
|
n |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
è |
|
|
n ø |
|
|
è |
|
|
|
ø |
è |
|
|
|
ø |
|
|
|
|
|
è |
|
ø |
|
|
|
è |
|
|
|
|
ø |
|
(*) |
|
|
|||||||||||||||||||||||||
|
1 |
|
æ |
|
|
1 |
ö |
|
|
æ |
|
n - 1ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
+ |
|
|
|
× ç |
1- |
|
|
|
÷ × ...× |
ç 1 |
- |
|
|
|
|
|
|
|
÷. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
n! |
|
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
è |
|
|
|
ø |
|
|
è |
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Каждая скобка положительна и ограничена сверху единицей, поэтому произведение скобок также ограничено сверху единицей. Отсюда
xn < |
2 + |
|
1 |
+ |
|
1 |
+ |
... + |
1 |
|
= 2 + |
|
1 |
+ |
|
|
1 |
|
|
|
+ |
... + |
|
|
1 |
|
|
|
< |
|
|
|
|
|
||||||||
|
|
|
3! |
n! |
1× 2 |
1× 2 × |
3 |
1× 2 × ...× |
n |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||||||||||||||||||
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|||
< 2 + |
+ |
+ |
|
+ ... + |
|
|
< 2 + |
+ |
|
+ |
|
+ |
... + |
|
+ |
+ ... = 2 + |
|
2 |
|
= 3 |
||||||||||||||||||||||
2 |
22 |
23 |
|
|
|
2n− 1 |
2 |
22 |
|
|
23 |
|
2n− 1 |
|
|
2n |
|
- |
1 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
24
