Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Университет им. Н.И. Лобачевского

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

15-10-2013_17-20-24 / Мои лекции по матем анализу 1 часть.pdf

Скачиваний:

151

Добавлен:

27.03.2015

Размер:

2.72 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2513 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

§6. Производная функции одной переменной

6.1. Определение производной функции в точке

Рассмотрим функцию f, заданную на множестве X, и принимающую действительные значения. Пусть х0 - внутренняя точка из области определения, т.е. она лежит в области определения

вместе с некоторой своей окрестностью ( $ U (x0 ) :U (x0 ) Ì X ).

Если х − точка из Х, то величина x = x − x0 называется

приращением переменной в точке х0, а величина

D f = f (x0 + D x) - f (x0 ) — приращением функции в точке х0.

Определение. Производной функции f (х)в точке x0

называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:

f '(x0 ) = lim			f (x0 +	x) − f (x0 )	.
f '(x0 ) = lim				x	.
x	→	0		x
	→

Замечание. Производная может быть как конечной, так и бесконечной. Пример . Функция y(x) = 3 x в точке х0 = 0 имеет бесконечную производную:

y'(0) = limx→ 0 3 0 + DDxx - 0 = + ¥ .

Примеры вычисления по определению производных некоторых основных элементарных функций

При вычислении следующих пределов используются известные эквивалентности. 1) Производная от константы f(x) = c.

f ¢(x) =

lim

c − c

= 0 .

x→ 0

D x

c′

2) Производная степенной функции f(x) = xα.

D x ö

- 1

D x

ç 1

× α ×

(x + D x)

- x

x ø

f ¢(x) =

lim

= lim

= α

× xα

− 1

D x

x→ 0

x→

(xα )′ = α × xα − 1

3) Производная показательной функции

f(x) = ax.

f ¢(x) =

lim

ax+ x - ax

= lim

ax × (a x - 1)

lim

× D x × ln a

× ln a

D x

x→ 0

x→

(a x )′

= a x × ln a;

(ex )′

= ex

4) f(x) = sin x.

D x ö

D x

D x ö

f ¢(x) = limsin(x +

D x) - sin x =

2 × cosç x +

× sinç

2 ×

cosç

cos x

lim

2 ø

lim

D x

→

D x

→

(в силу непрерывности функции cos x).

(sin x)′ = cos x

f(x) = cos x.

x +

D x ö

cos(x +

D x) -

cos x

2× sinç

× sinç

f ¢(x) = lim

lim

2 ø

D x

x→

D x

x +

D x ö

2×

× sinç

lim

= - sin x.

D x

x→ 0

(cos x)′ = − sin x .

6.2.Односторонние производные. Связь непрерывности функции в точке

ссуществованием конечной производной

Пусть f : X → R , x0 X.

Определение. 1) Если функция определена в левосторонней окрестности точки x0 , то

f−¢ (x0 ) = lim	f (x0 + D x) - f (x0 )	- производная слева функции f	в точке x0 .
	D x
x→ 0− 0

2). Соответственно, если функция определена в правосторонней окрестности точки x0 , то

f+¢ (x0 ) = lim	f (x0 + D x) - f (x0 )	- производная справа функции f	в точке x0 .
	D x
x→ 0+ 0

По теореме о связи существования предела и односторонних пределов: $ f ′(x0 ) = A Î R Û $ f−′ (x0 ) = f+′ (x0 ) = A .

Теорема (о связи непрерывности функции в точке с существованием конечной производной).

Если функция имеет конечную производную в точке, то она непрерывна в этой точке.

Доказательство. По условию $ lim

f (x0 +

D x) - f (x0 )

= A Î R .

Поэтому

x→

D x

limD f

= lim( f (x0

+ D x) -

f (x0 )) =

lim

f (x0 + D x) -

f (x0 )

× D x =

A × 0 = 0.

D x

x→ 0

x→

x→ 0

Значит, по определению, f (x)

непрерывна в точке x0 . ■

Обратное не верно. Как показывает следующий пример, функция, непрерывная в

точке, может не иметь производной в этой точке.

Пример 1. Функция

f(x) = |x| в точке x0 = 0 непрерывна, т.к.

lim f (x) = 0

lim f (x) =

f (0) =

0 .

x→ 0− 0

x→ 0+ 0

Найдем ее односторонние производные в этой точке:

f−¢ (0) =

lim

f (D x) -

f (0)

lim

D x

lim

D x ö

ç -

÷ =

- 1;

D x

x→ 0− 0

D x ø

f+¢ (0) =

lim

f (D x) -

f (0)

lim

D x

lim

D x

= 1.

D x

x→ 0+ 0

D x

x→ 0− 0

f ′(0) .

Так как

f−′ (0) ¹

f+′ (0) , то не существует производной

x × sin

x ¹ 0

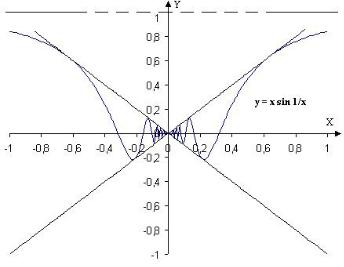
Пример 2. y(x) =

x =

lim y(x) =

1 ö

= 0

limç x × sin

x→ 0

x→ 0è

x ø

(так как

x — б.м., а

sin 1

- ограничена).

Так как

lim y(x) =

y(0) Þ

, то

x→ 0

y(x) непрерывна в точке x0 =

0 .

В то же время,

y(D x) - y(0)

D x × sin

= lim sin

не существует.

y'(0) = lim

lim

D x

x→ 0

D x

При x → ∞ у функции y(x) существует асимптота y = 1.

6.3. Правила вычисления производной. Таблица производных

	Правила вычисления производной
Пусть	f ′(x) R, g′(x) R . Тогда
1) (c × f (x))′ =	c( f (x))′ , где c – число.

2)( f (x) + g(x))′ = ( f (x))′ + (g(x))′ .

3)( f (x) × g(x))′ = ( f (x))′ × g(x) + f (x) × (g(x))′ .

4)	æ	f (x) ö		′	( f (x))¢ × g(x) - f (x) × (g(x))¢		, где g(x)¹0.
	ç		÷	=
						2
	ç	÷			(g(x))
	è	g(x) ø

5) Производная сложной функции

( f (g(x)))′ = f ¢(g(x)) × g¢(x) .

6)Производная обратной функции

( f − 1 )′ ( y0 ) =

где y0 = f (x0 )

, f’(x0)¹0, f − 1( y)

непрерывна в точке y0 .

f ¢

(x0 )

Доказательство.

Свойства 1) и 2) предлагается проверить самостоятельно.

( f (x)× g(x))¢ =

lim

f (x +

D x)× g(x +

D x) -

f (x)× g(x)

D x

x→

lim

f (x +

D x)× g(x +

D x) -

f (x)× g(x +

D x) +

f (x) × g(x +

D x) -

f (x)× g(x)

D x

x→ 0

lim

g(x +

D x) × (

f (x +

D x) -

f (x))

+ lim

f (x) × (g(x + D x)

g(x))

D x

x→ 0

D x

lim g(x +

D x) × lim

f (x + D x) - f (x)

lim f

(x)× lim

g(x +

D x)

g(x)

D x

x→ 0

D x

x→ 0

= ( f (x))′ × g(x) + f (x) × (g(x))′ .

Здесь использовалось то, что если функция g(x) имеет конечную производную в точке, то она

непрерывна в этой точке и

lim g(x + x) = g(x) .

x→ 0

f (x) ö ¢

f ( x +

f (x)

g( x + D x)

g(x)

lim

D x

g(x) ø

x→ 0

		æ	1		f ( x + D x) × g( x) - f (x) × g( x + D x) ö
	limç					÷
=		ç		×			÷	=
	x→ 0	è	g( x + D x) × g(x)		D x	ø
		æ	1		f ( x + D x) × g( x) - f (x) × g(x) + f (x) × g(x) - f (x) × g( x + D x) ö
	limç							÷
=		ç		×					÷	=
	x→ 0	è	g( x + D x) × g(x)			D x		ø

f ( x + D x) - f (x) ö

g( x + D x) - g(x) ö ö

lim

ç lim

g(x) ×

lim

f (x) ×

x→ 0 g

( x + D x) ×

D x

÷ -

D x

÷ ÷ =

g(x) è

x→ 0 è

ø ø

( f (x))¢

× g(x) -

f (x) × ( g(x))¢

, ч.т.д.

( g(x))2

( f ( g(x)))¢

= lim

f ( g( x +

x)) −

f ( g(x))

D x

→ 0

g →

Обозначим

g =

g( x +

x) − g(x) . Тогда

при

x → 0

в силу непрерывности

функции g(x) . Поэтому

lim

f ( g( x + D x))

- f ( g(x))

f ( g(x + D x)) - f ( g(x))

x + D x) - g(x) ö

limç

÷ =

x→ 0

D x

x→ 0 è

g( x + D

x) - g(x)

D x

lim

f ( g(x) +

g) − f ( g(x))

× lim

g( x + x) −

g(x)

f ¢(g(x))× g¢(x) .

D x

g→ 0

D g

x→ 0

6) (

f − 1 )¢ ( y0 ) =

lim

f − 1 ( y0 +

D y) -

f − 1 ( y0 )

(*)

D y

y→ 0

Так

как

y0 = f ( x0 ) ,

то

f − 1 (y0 ) =

x0 .

Обозначим

x = x − x0 =

f − 1(y0 +

y) −

f − 1(y0 ) →

при

y →

0 , т.к.

При этом Dy = f(x) - f(x0). Поэтому из (*):

( f −

1 )¢( y0 ) = lim

f (x0 )

f (x0 + D x) - f

(x0 )

f ¢( x0 )

x→ 0 f (x) -

lim

D x

x→ 0

x = f − 1 ( y0 + D y) .	Тогда
f − 1 Непрерывна.

. ■

Примеры.

(tgx)′

cos2 x

По правилу 4) получаем:

Доказательство.

(tgx)

sin x ö

′

(sin x)′ × cos x - sin x × (cos x)′

cos2

x +

sin 2 x

. ■

cos2 x

cos

2 x

cos2

cos x ø

(ctgx)′

−

sin2

Также по правилу 4):

Доказательство.

(ctgx)

cos x

ö ′

(cos x)′ × sin x -

cos x × (sin x)′

- sin2

x - cos2 x

= -

. ■

sin x

sin

2 x

sin 2 x

sin2

(loga x)¢ =

(ln x)¢

1 .

x ×

ln a

Доказательство. По правилу 6):

f ¢( x0 ) =

нас

f (x) =

log

x =

y ,

( f − 1 )¢

( y0 )

значит x =

− 1

( y) . Поэтому

(loga

x)¢

. ■

(a y

)¢

a y × ln a

x ×

ln a

(arctgx)′ =

Снова

применяя

правило

для

функции

f (x) = arctg x = y ,

Доказательство.

x = tg y =

f − 1 ( y) , получаем:

(arctgx)¢ =

(tgy)¢

1+ tg2 y

+ x2 . ■

cos2

(arcctgx)′

−

1 +

Доказательство.

Опять

по

правилу

для

f (x) = arcctg x =

y ,

x =

ctg y =

f − 1 ( y) :

(arcctgx)¢

= -

(ctgy)¢

1+ ctg2 y

1+ x2

■

- sin 2

(arcsin x)′

1 −

Доказательство. Снова по правилу 6):

y = arcsinx ,

x = sin y при

y <

Тогда |x|<1, и

(arcsinx)¢

■

(sin y)¢

cos y

sin 2

(arccos x)¢

Доказательство.

По

правилу

6):

y = arccos x ,

x = cos y

при

0 < y < π

|x|<1

(arccos x)¢

(cos y)¢

sin y

cos2

x2 .

■

8)(shx)′ = chx .

				æ	ex - e− x ö		′	ex + e− x
	Доказательство. (shx)¢		=	æ	ex - e− x ö		′	ex + e− x	=	chx .	■
	Доказательство. (shx)¢		=	ç		÷	=		=	chx .	■
				ç	2	÷		2
				è	2	ø		2
9)	(chx)′ = shx	.
				æ	ex + e− x ö		′	ex - e− x
	Доказательство. (chx)¢		=	æ	ex + e− x ö		′	ex - e− x	=	shx .	■
	Доказательство. (chx)¢		=	ç		÷	=		=	shx .	■
				ç	2	÷		2
				è	2	ø		2

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2513 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке 15-10-2013_17-20-24

#
27.03.201529.7 Кб32Коллоквиум1.doc
#
27.03.20152.72 Mб151Мои лекции по матем анализу 1 часть.pdf