Пример: limx2

=

+ ¥

x→ ∞

> δ Þ x2 > ε

" ε > 0

$ δ > 0 : " x Î R

x

x

>

δ

=

.

ε

ε

Случай 15. a = ¥,

A = -¥.

lim f (x) = - ¥

Û

[" ε > 0

$ δ = δ (ε ) > 0 : " x Î X

| x |> δ

Þ

f (x)< - ε ] .

x→ ∞

Здесь ε и δ - большие числа.

Пример. lim(- x2 + 5) = - ¥

x→ ∞

> δ Þ (- x2 + 5) < - ε

" ε > 0

$ δ > 0 : " x Î R

x

x2 > ε + 5

x

>

δ =

ε + 5

ε + 5.

Случай 16. a = ¥,

A = ¥.

lim f (x) = ¥

Û [" ε

> 0

$ δ = δ (ε ) > 0 : " x Î X

| x |> δ

Þ

| f (x) |> ε ] .

x→ ∞

Здесь ε и δ - большие числа.

Пример. limx3

=

¥

x→ ∞

" ε > 0

$ δ > 0 : " x Î R

x

> δ Þ

x3

> ε

x

>

3

δ

= 3

.

ε

ε

функции f

в точках xn сходится к A , то есть

lim f (x) =

A Û [" {xn } Ì X \ {a} xn ® a (n ® ¥ ) Þ f (xn ) ® A (n ® ¥ )] .

x→ a

Пример. Используя определение предела по Гейне, докажем, что lim(x2

+ 3x) = 4 .

x→ 1

имеем xn

2 ® 1, 3 × xn ® 3, xn

2 + 3× xn ® 4 , то есть f (xn) ® 4.

4.2. Свойства пределов функций

Доказательство. Пусть lim f (x) = A и lim f (x) = B . Тогда, согласно определению предела

x→ a

x→ a

по Гейне: " {xn } Ì X \{a} xn ®

a (n ® ¥ ) Þ f (xn ) ® A (n ® ¥ ) и f (xn ) ® B (n ® ¥ ) .

Пример. Покажем, что предел

lim

sin x

не существует.

x ∞

Возьмем последовательность

xn =

π

+ 2π n, nÎ N . Тогда xn →

+ ∞ ( n → ∞ ), и

π + 2π n) = 1 ® 1 (n ®

2

sin(xn ) = sin(

¥ ) .

2

~

~

Теперь возьмем другую последовательность xn

= π n, nÎ N . Тогда тоже xn ® + ¥ (n ® ¥ ) , но

~

¥ ) .

sin(xn ) = sin(π n) = 0 ® 0 (n ®

~

lim sin(xn ) ¹ limsin(xn )

, то общего предела у функции sin x при x®+¥ нет.

Так как n→ ∞

n→ ∞

Теорема 2. (Об ограниченности функции, имеющей конечный предел.)

Функция, имеющая конечный предел в точке из расширенной числовой прямой

,

R

ограничена в некоторой окрестности этой точки.

lim f (x) =

AÎ R

Доказательство. Пусть aÎ R ,

. Покажем, что найдется окрестность U(a)

x→ a

точки a, в которой функция f ограничена, то есть $ m,M Î R :

" x Î X Ç U (a)

m £ f (x) £

M .

В силу определения предела по Коши для ε = 1

$ Uδ (a) : " x Î (X \{a}) Ç Uδ (a)

f (x)Î Uε

(A) ,

то есть " x Î

X Ç Uδ (a) x ¹

a Þ

A - 1 <

f (x) <

A + 1.

lim

f x B

(или

lim

f

x B

). Тогда

Теорема 3. Пусть x a

x a

$ U (a) : " x Î X

B (соответственно

f(x) > B).

Ç U (a) f (x) <

Доказательство. По определению предела, если

lim f (x) = A , то для ε

= B - A > 0

x→ a

$ U (a) : " x Î X

- A |<

B -

A . Поэтому f(x) < A + (B-A) = B. Ч.т.д. ■

Ç U (a) | f (x)

Теорема 4 (о переходе к пределу в неравенстве).

$ lim f (x) = A

$ lim g(x) = B

Пусть

$ U (a) : " x Î U (a) Ç X f

Ç X g

f (x) £

g(x)

, и

,

.

x

→ a

x→ a

Тогда A £ B.

Доказательство (методом от противного).

A +

B

Допустим, что A > B. Тогда, так как lim f (x) =

A >

, то по предыдущей теореме

$ U1 (a) : " x Î U 1 (a) f (x) > A + B .

x→ a

2

2

A +

B

Аналогично, так как lim g(x) = B <

, то по предыдущей теореме

2

x→ a

$ U2 (a) : " x Î U 2 (a) g(x) < A + B .

2

f (x) >

A +

B

> g(x) , то есть f(x)> g(x).

Поэтому " x Î U (a)Ç U 1 (a) Ç U 2 (a)

2

f (x) £

g(x) , значит A £

B . ■

Получили противоречие с условием " x Î U (a)

Пусть $ U (a) : " x

lim f (x) =

lim h(x) =

A

.

Î U (a) Ç X f Ç

X g Ç Xh f (x) £ g(x) £ h(x) , и x→ a

x→ a

Тогда $ lim g(x) =

A .

x→ a

Доказательство. Зафиксируем e > 0. Тогда, по определению предела lim f (x) = A ,

x→ a

$ U1 (a) : " x Î X Ç U

1 (a)

| f (x) -

A |< e

, а значит f(x) > A-e.

Аналогично, по определению предела

lim h(x) = A ,

x→ a

$ U2 (a) : " x Î X Ç U

2 (a)

| h(x) -

A |< e

, а значит h(x) < A+e.

Поэтому " x Î X

(a) Þ

A - e < f (x) £

g(x) £ h(x) < A + e , то есть

x Î U (a) = U 1 (a) Ç U 2

lim g(x) =

A

" x Î

X Ç U (a) | g(x) - A |< e . Следовательно,

. ■

x→ a

Теорема 6 (об арифметических действиях над пределами).

Пусть lim f (x) =

AÎ R,

lim g(x) = B Î R . Тогда

x→ a

x→ a

1)

lim( f (x) +

g(x)) =

A +

B

x→ a

2)

lim( f (x)×

g(x)) =

A×

B

x→ a

3)

lim

f (x)

=

A

, если B ¹ 0 .

x→ a g(x)

B

Теорема 7

(о пределе композиции).

Пусть f : X →

Y,

g : Y → Z ,

lim f (x) = A,

limg(y) = B , и при x ¹ a f(x) ¹ A. Тогда

lim g( f (x)) =

x→ a

y→ A

B .

x→ a

последовательность {xn} из Х\{a}, сходящуюся к a. Тогда, так как

lim f (x) = A , то

x→ a

f (xn ) ® A (n ® ¥ ) . Отсюда, так как

yn = f(xn) →

A и lim g(y) =

B , получаем, что

y→

A

g( f (xn )) → B (n → ∞ ) .

Итак, " {xn } Ì X \{a} xn ® a (n ® ¥ )

Þ f (xn ) ®

A (n ®

¥ ) .

limsin x

= 1

.

x→ 0

x

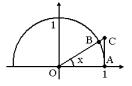
Доказательство. Пусть 0 < x <

π

. На окружности радиуса 1 с центром O в начале координат

2

S OAB <

Sсектора OAB <

S OAC .

1

sin x <

1

2

x

1

× 1× tg x .

2 ×1× 1×

2

×1 ×

<

2

Умножив это неравенство на

2

> 0 , получим:

sin x

1<

x

<

1

,

откуда

cos x <

sin x

< 1.

sin x

cos x

x

π < x < 0 .

Так как в каждой части неравенства функции четные, оно выполняется и при −

Итак, $ U (0) = (- π ,

π

) : " x Î U (0)

cos x <

sin x

2

< 1 , и limcos x = 1. Тогда, согласно теореме 5

2

2

x

x→ 0

о трех функциях,

$ lim sin x

= 1. Ч.т.д. ■

x→ 0

x

Полезные пределы, следующие из I замечательного предела.

1)

lim tg x =

1.

x→ 0

x

tg x

1

sin x

Доказательство. lim

=

lim

æ

×

ö

= 1 . Ч.т.д. ■

ç

÷

x

cos x

x

x→

0

x→

0

è

ø

2)

lim arcsin x

=

1

x→ 0

x

Доказательство. Замена x = sin y , y =

arcsin x →

0 при x → 0 .

lim arcsin x

= lim

y

= 1 .Ч.т.д. ■

sin y

x→ 0

x

y→ 0

3)

lim arctg x = 1

x→ 0

x

Доказательство аналогично пункту 2). ■

Второй замечательный предел

1)x = e;

1

lim(1+

lim(1+ x) x

=

e.

x→ ∞

x

x→

0

Доказательство.

1)

Докажем сначала для x →

+ ∞ . Для любого xÎR из неравенства [x] ≤ x ≤

[x] + 1

(где [x] – целая часть числа x) вытекает неравенство

æ

1

ö

[ x]

æ

1 ö x

æ

1

ö [ x]+ 1

,

ç 1+

÷

<

ç

1+

÷

< ç

1+

÷

ç

÷

è

x ø

ç

÷

откуда

è

[x] + 1ø

è

[x] ø

æ

1

ö [ x]+ 1

æ

1

ö − 1

æ

1

ö

x

æ

1 ö [ x]

æ

1 ö

(*)

ç 1

+

÷

×

ç 1

+

÷

<

ç 1+

÷

<

ç

1+

÷

× ç 1 +

÷