Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Университет им. Н.И. Лобачевского

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

15-10-2013_17-20-24 / Мои лекции по матем анализу 1 часть.pdf

Скачиваний:

151

Добавлен:

27.03.2015

Размер:

2.72 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2512 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

§5. Непрерывность функции

5.1. Определение непрерывности функции в точке

Пусть функция f задана на множестве D Ì R и принимает действительные значения, x0 - точка из D.

Определение. Функция f непрерывна в точке x0 тогда и только тогда, когда предел

функции в этой точке равен значению функции в этой точке, т.е. $ lim f (x) = f (x0 ) . В этом

x→ x0

случае x0 называется точкой непрерывности.

В противном случае, а также, если функция не определена в этой точке, функция f называется разрывной в точке x0 (а сама x0 - соответственно, точкой разрыва).

Подставляя сюда определения предела по Коши или по Гейне, получим: Определение непрерывности функции в точке по Коши:

f (x)

непрерывна в точке x0

" ε > 0

$ δ >

0 : " x Î D

x - x0

< δ Þ

f (x) - f (x0 )

< ε .

Определение непрерывности функции в точке по Гейне:

f (x)

непрерывна в точке x0

" {xn }n N Ì D

xn ® x0 Þ

f (xn ) ® f (x0 ) .

Из связи существования предела и односторонних пределов получаем:

Критерий непрерывности функции в точке через односторонние пределы.

f (x) непрерывна в точке x0 Û существуют f (x0 - 0) и f (x0 + 0) , равные f (x0 ) .

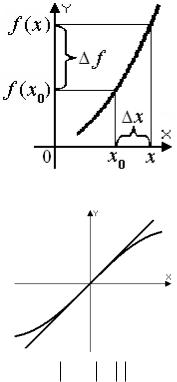
Разность D x = x - x0 называется приращением переменной.

Разность D f = f (x) - f (x0 ) - называется приращением функции.

Критерий непрерывности функции в точке через приращения.

f (x) непрерывна в точке x0

limD

0 .

x→ 0

Пример 1.

f (x) = c =

const непрерывна в любой точке x0 R , так как

" ε > 0

$ δ

> 0 : " x Î

x -

< δ Þ

c - c

ε - верно.

Пример 2.

f (x) = sin x

также непрерывна в любой точке x0 R ,

так как

" ε

> 0

$ δ >

0 : " x Î

x -

< δ

sin(x) - sin(x0 )

< ε .

Чтобы доказать это, оценим последний модуль, используя

тригонометрию и неравенства |sin t| £ |t|

|cos t| £1 для

t R :

sin(x) - sin(x0 )

2× sin

x - x0

× cos

x +

2×

x - x0

×1 =

x - x0

Поэтому в качестве δ можно взять δ

. ■

sin t < t

Определение непрерывности функции на множестве.

Функция f : D → R непрерывна на множестве G Ì D тогда и только тогда, когда она непрерывна в каждой точке множества G.

Свойства непрерывных функций

Верна следующая теорема:

Теорема 1. Все основные элементарные функции непрерывны на своей области определения.

Теорема 2 (об арифметических действиях над непрерывными функциями).

Пусть функции f и g непрерывны в точке x0 . Тогда функции f + g, f · g и	f	(если g(x0)¹0)
	g	(если g(x0)¹0)
	g
также непрерывны в точке x0 .

Примеры.

1)Многочлен Pn(x) = anxn +…+ a1x + a0 непрерывен в любой точке действительной оси, так как он является суммой непрерывных функций (одночленов).

2)Рациональная функция – это отношение двух многочленов:

	P (x)		a	n	xn + ... +	a x +	a	0
R(x) =	n	=		n		1		0	. Она непрерывна в тех точках x, где Qm(x)¹0.
R(x) =	Q (x)	=	b xm + ... +			b x +	b		. Она непрерывна в тех точках x, где Qm(x)¹0.
	Q (x)		b xm + ... +			b x +	b
	m		m			1		0

Теорема 3 (о непрерывности композиции).

Пусть функция f задана на множестве X и принимает значения во множестве Y, а функция g задана на множестве Y. Тогда если функция f непрерывна в точке x0ÎX, и функция g

непрерывна в точке f (x0)ÎY, то функция g( f ) также непрерывна в точке x0. Доказательства теорем 2 и 3 следуют из соответствующих теорем о пределе функции. ■

Теорема 4. Если функция задана, возрастает и непрерывна на промежутке X, то множество Y ее значений также является промежутком. На Y определена обратная функция, которая также возрастает и непрерывна.

Без доказательства .

Приведем еще одну важную для вычисления пределов теорему:

Теорема 5 (о пределе степенно-показательного выражения).

Пусть существуют конечные пределы	lim f (x) = A > 0	и	lim g(x) = B . Тогда существует
	x→ x0		x→ x0

предел lim f (x)g( x) = AB .

x→ x0

Доказательство. Функцию f(x)g(x) можно представить в виде e g x ln f x . Так как f(x)®A (x®x0), и логарифмическая функция непрерывна, то ln f (x) ® ln A (x®x0). Тогда, по теореме 2, g(x)×ln f(x) ® B×ln A при x®x0. Откуда, в силу непрерывности показательной функции,

e g x ln f x eB ln A=AB при x®x0. ■

Следствие. Если функции f(x) и g(x) непрерывны в точке x0, и f(x0 )>0, то функция f(x)g(x)

также непрерывна в точке x0, то есть	lim f (x)g ( x) =	f (x )g ( x0 )	.
	x→ x0	0

5.2. Точки разрыва функции и их классификация

Пусть функция f определена в некоторой окрестности точки x0 , кроме, быть может, самой точки x0 . Точка x0 называется точкой разрыва функции f, если f либо не определена в этой точке, либо x0 не является точкой непрерывности. Классифицируем точки разрыва в зависимости от поведения в них односторонних пределов:

Определение. Точка x0 называется точкой разрыва I рода, если в этой точке существуют конечные односторонние пределы (возможно разные), т.е. f ( x0 − 0 ), f ( x0 + 0 ).

При этом величина

f ( x0 +

0 ) − f ( x0 −

0 ) называется скачком функции f в точке x0 .

Пример 1. Определим тип точки разрыва x0

= 0 у функции

x >

- 1,

x <

0 .

y = sign x = í

x =

y(x0

− 0) =

− 1

. Следовательно, x0 =

0 - точка разрыва I рода.

y(x0

+ 0) = 1Î R

Пример 2. Определим тип точки разрыва

= 0 у функции y = arctg

1 .

Если x ®

0 - 0, то

- ¥ Þ

arctg

, y(0 - 0) = -

;

Если x ®

0 + 0 то

+ ¥ Þ

arctg

y(0 + 0) =

Поэтому x0

= 0 - точка разрыва I рода.

Частный случай точки разрыва I рода:

Определение. Если пределы в точке слева и справа одинаковы, то она называется точкой устранимого разрыва.

Если x0

- точка устранимого разрыва, то достаточно изменить (или определить)

функцию лишь в этой точке, чтобы функция стала непрерывной в точке x0 (устранить

разрыв).

ì 1,

x ¹

Пример 3.

y =

signx

= í

x =

x0 =

î 0,

0 - точка устранимого разрыва.

Для устранения разрыва достаточно взять y(0) = 1.

Определение. Точка разрыва x0

называется точкой разрыва II рода, если она не является

точкой разрыва I рода, то есть хотя бы один из односторонних пределов бесконечен или

вообще не существует.

Пример 4.

y =

2 x , x0

= 0. Выше было вычислено, что

при x → 0 − 0

y →

0 , а при x → 0 + 0

y → + ∞ .

Поэтому y(0-0) = 0, y(0+0) = +¥. Значит x0

= 0 - точка разрыва II рода.

Пример 5.

y =

sin 1 ,

x0 =

Покажем по определению Гейне, что предел y(0+0) не существует.

Возьмем xn

, n Î N . Тогда xn Î (0,+ ¥ ), xn ® 0 (n ® ¥ ) , и

+ 2π n

y(xn ) = sin(

+ 2π n) = 1 ® 1 (n ®

¥ ) . Теперь возьмем другую последовательность

xn =

, n Î

. Тогда тоже

xn Î

(0,+ ¥ ), xn

® 0 (n ® ¥ ) , но y(xn ) = sin(π n) = 0 ® 0 (n ® ¥ ) .

π n

Так как

lim y(xn ) ¹ lim y(xn )

, то предел справа y(0+0) не существует.

n→ ∞

Значит x0 =

0 - точка разрыва II рода.

5.3. Свойства функций, непрерывных на отрезке.

Напомним, что функция f (x) называется непрерывной на отрезке [a,b], если она

непрерывна в каждой точке этого отрезка. Множество всех функций, непрерывных на отрезке [a,b], обозначается C [a,b].

Теорема 1 (Первая теорема Больцано-Коши).

Если функция непрерывна на отрезке и принимает на концах этого отрезка значения разных знаков, то внутри этого отрезка найдется точка, в которой функция обращается в нуль (т.е.

если f (x)

непрерывна на [a,b] ,

f (a) × f (b) <

0 , то $

c Î (a,b) : f (c) = 0 ).

Доказательство.

Шаг 1. Поделив отрезок [a,b] пополам, получим два отрезка:

a + bù

é a + b

æ a + b ö

с =

a + b

, теорема

ê a,

и ê

,bú . Если

f ç

÷ = 0 , то

доказана. А если нет, то из двух половинок обязательно найдется отрезок, на концах

которого функция принимает значения разных знаков. Обозначим его [a1 ,b1 ] . Тогда

f (a1 ) ×

f (b1 ) <

0 , длина отрезка [a1 ,b1 ] равна

b −

æ a1

+ b1 ö

Шаг 2. Теперь делим пополам отрезок [a1 ,b1

] . Если

0 , то

с =

+ b1

, теорема

f ç

доказана. А если нет, то выбираем из двух половинок такой отрезок [a2 ,b2 ] , на концах

которого значения функции имеют разные знаки: f (a2 ) ×

f (b2 ) <

0. Длина [a2 ,b2 ]

равна

b1 − a1

b −

Далее продолжаем процесс деления. На n -м шаге снова: либо найдем с, либо получим

отрезок [an ,bn ] , такой что

f (an )× f (bn ) < 0 . Длина [an ,bn ] равна

b − a

0 при n →

∞ .

Таким образом, либо найдем с на каком-либо шаге, либо получим систему вложенных

отрезков [a,b] É [a1 ,b1 ] É [a2 ,b2 ] É

... É [an ,bn ] É

[an+ 1 ,bn+ 1 ] É

... со стремящимися к нулю

длинами. В первом случае теорема доказана.

Во втором случае из теоремы Кантора о вложенных отрезках следует, что $ !c :

" n Î N c Î [an ,bn ] . Так как длины отрезков стремятся к нулю, то

® c

и b

® c .

Поэтому, в силу непрерывности функции f,

f (an ) ®

f (c) и

f (b

) →

f (c) . Значит

f (an )×

f (bn ) ®

f 2 (c) . Так как" nÎ

N f (an )×

f (bn ) < 0 , то

f 2 (c) = lim f (an )× f (bn ) £

0 .

n→ ∞

Следовательно, f (c) = 0 . ■

Замечание 1. Точек, в которых функция обращается в ноль, может быть несколько (см. рисунок).

Замечание 2. Если функция монотонно возрастает, то такая точка единственна.

Геометрический смысл этой теоремы очень прост: непрерывная линия, соединяющая две точки, лежащие по разные стороны оси ОХ, обязательно пересекает эту ось.

Приведенное доказательство ценно тем, что в нем содержится метод приближенного поиска корней уравнения f(x)=0 (метод половинного деления).

где a2n +1

+a2nx2n +…+a0,

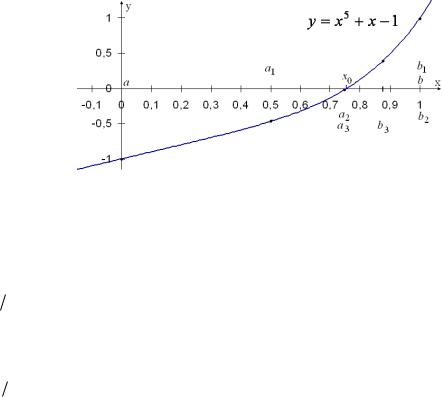
Пример. Приближенно решить методом половинного деления уравнение x5 + x − 1 = 0 . Решение. Возможные рациональные корни: 1 и -1. Ни один из них не подходит. Поэтому все

корни, если они есть,

иррациональны.

Положим f (x) = x5 + x - 1. Функция

возрастает, как сумма двух

возрастающих функций, поэтому

уравнение имеет не более одного

действительного корня.

Так как f непрерывна на R и

f (0) =

- 1, f (1) = 1, то по доказанной

теореме внутри отрезка [0; 1]

найдется точка x0 , в которой функция обращается в нуль. Вычислим ее.

0 + 1

Шаг 1.

Середина отрезка:

; значение функции: f ç

- 1 <

0 ,

значит x0 Î [1 ,1] .

1 2 + 1

3 ö

243

- 13

Шаг 2.

Середина отрезка:

; значение функции: f ç

- 1 =

0 ,

1024

x0 Î [3

значит

,1] .

3 4 + 1

7 ö

16807

12711

Шаг 3.

Середина отрезка:

- 1

> 0

; значение функции: f ç

32768

значит

x0 Î [

, 7], то есть 0,75 <

x0 < 0,875 .

И т.д. В качестве приближенного значения можно взять середину последнего отрезка:

(0,75+0,875)/2=0,8125, поэтому x0 =

0,8125 ± 0,0625 . ■

Пример 2. Любой многочлен нечетной степени P(x) = a2n +1x2n +1

¹0, имеет хотя бы один действительный корень.

Доказательство. Запишем P(x) в виде x2n +1(a2n +1 + a2n /x + …+ a0/x2n +1). Отсюда видно, что при достаточно больших положительных значениях переменной х знак P(x) совпадает со знаком a2n +1, а если х - достаточно большое отрицательное, то знак P(x) противоположен знаку a2n +1. Поскольку многочлен непрерывен на всей действительной прямой, то по первой теореме Больцано-Коши найдется промежуточная точка с, в которой P(x) обращается в ноль. ■

Теорема 2 (Вторая теорема Больцано-Коши).

Если функция непрерывна на отрезке [a,b], то она принимает любое промежуточное

значение между	f (a)	и f (b) .	f (a) < f (b) . Покажем, что k ( f (a), f (b))
Доказательство. Допустим, что
$ c Î [a,b]: f (c) =	k ). Введем вспомогательную непрерывную функцию g(x) = f (x) - k .
Тогда g(a) = f (a) - k <		0 , g(b) =	f (b) -	k > 0 . Поэтому по Теореме 1 $ c Î [a,b]: g(c) = 0 ,
значит f (c) - k =	0 Þ	f (c) = k . Случай		f (a) больше f (b) рассматривается аналогично. ■

Теорема 3 (первая теорема Вейерштрасса).

Если функция определена и непрерывна на отрезке, то она ограничена на этом отрезке ( т.е. если fÎC[a,b], то $ M Î R,$ m Î R : m £ f (x) £ M " x Î [a,b] ).

Доказательство. От противного. Допустим, что функция не ограничена сверху.

Тогда n N xn [a , b]: f xn ≥n . Последовательность xn ограничена, так как лежит на

отрезе [a , b]			. По теореме Больцано-Вейерштрасса из нее можно выбрать сходящуюся
подпоследовательность xnk x0 , где x0 [a ,b ] . Поскольку функция f непрерывна в точке
x	0 , то	f xn	f x0	. Но это противоречит тому, что	n N	f xnk ≥nk	. Поэтому
		k			k
функция ограничена сверху.
		Аналогично доказывается ограниченность снизу. ■

Теорема 4 (вторая теорема Вейерштрасса).

Если функция определена и непрерывна на отрезке, то она достигает на нем своих точной верхней и точной нижней граней.

Доказательство. Пусть функция f определена и непрерывна на отрезке [a , b] . По первой

теореме Вейерштрасса функция ограничена, поэтому существуют конечные	m = inf f (x)	и
	x [a,b]

M = sup f (x) . Нужно показать, что они достигаются в некоторых точках отрезка, то есть
x [a,b]
x1 [a,b], x2 [a,b]: f (x1) = M , f (x2 ) = m .			M = sup f (x)
Докажем это методом от противного. Предположим, что значение			M = sup f (x)	не
			x [a,b]
достигается. Тогда x [a , b] f x M . Поэтому функция x =			1
достигается. Тогда x [a , b] f x M . Поэтому функция x =			M − f x
			M − f x
на отрезке [a ,b] непрерывна и положительна. По предыдущей теореме она ограничена,
поэтому K : x[a ,b] 0 x =	1	≤K . Отсюда x[a ,b] f x ≤M −			1	,
поэтому K : x[a ,b] 0 x =	M − f x	≤K . Отсюда x[a ,b] f x ≤M −			K	,
	M − f x				K

значит число М не является наименьшей верхней границей, то есть супремумом. Полученное противоречие показывет, что наше предположение неверно, и супремум достигается. ■

Можно привести другое доказательство этих теорем:

Теорема 3-4 (первая и вторая теоремы Вейерштрасса).

Если функция непрерывна на отрезке, то она ограничена на этом отрезке и достигает на нем

своих точных верхней и нижней граней ( т.е. если f C[a,b], то M = sup					f (x) R , и
c [a,b] : f (c) = M ).				x [a,b]
c [a,b] : f (c) = M ).
Доказательство. 1) Сначала докажем, что M = sup f (x)				(либо конечный, либо + ∞ )
достигается, т.е. c [a,b]: f (c) = M .			x [a,b]
достигается, т.е. c [a,b]: f (c) = M .					n N an < M
Возьмем последовательность	{a	}	n N , сходящуюся к М, такую что		n N an < M	.
Возьмем последовательность	n		n N , сходящуюся к М, такую что			.

Поскольку М - наименьшая верхняя граница, то n an не является верхней границей, значит xn [a,b]: f (xn ) > an .

По теореме Больцано-Вейерштрасса из ограниченной последовательности xn можно

выбрать сходящуюся подпоследовательность			xn k с , где с[a ,b] . Поскольку функция f
непрерывна в точке с, то f xn k f с при k →				+ ∞ .
Так как при всех k ank < f (xnk		)	≤ M , то по теореме о трех последовательностях
получаем: f xn k M при k → + ∞ .
Итак, f (c) = M =	sup f (x) .
	x [a,b]
2) Теперь докажем, что	sup f (x) конечен:	sup		f (x) = f (c) R , поэтому конечен. Ч.т.д. ■
	x [a,b]	x [a,b]

Замечание. Из теорем 2 и 4 следует, что непрерывная функция на отрезке, принимает все промежуточные значения между

m =	inf	f (x)	и	M = sup	f (x)	.
	x [a,b]		и	x [a,b]		.

Следствие. Непрерывный образ отрезка есть отрезок. Пусть fÎC[a,b],							m = inf f (x) и
							x [a,b]
M =	sup	f (x) , тогда значения функции заполняют отрезок [m,M].
	x [a,b]

Понятие равномерной непрерывности.

Пусть функция непрерывна на промежутке X. Это значит, что для любой точки x0 X

илюбого ε > 0 найдется δ > 0, δ = δ(x0, ε), зависящее от точки x0 и от ε, такое что x - x0 < δ Þ f ( x) - f ( x0 ) < ε .

Понятие равномерной непрерывности – это более сильное ограничение на функцию. Определение. Функция f(x) равномерно непрерывна на промежутке X, если для

любого ε > 0 найдется δ > 0, δ = δ(ε), зависящее только от ε, такое что " x1 Î

X , " x2 Î X , что

x - x0

< δ Þ

f ( x) - f ( x0 )

< ε .

Если функция равномерно непрерывна на промежутке X, то она также является

непрерывной на нем. Обратное неверно, как видно из следующего примера.

Пример. f (x) = sin

X =

ú .

; x¢

(2n + 1)π

n .

f ( x

) =

sinæ

+ π n

= (- 1)n

f ( x′

)

;

= sin πn = 0.

( x

) - f

( x¢

)

= 1

| x

x¢

n(2n +

1)× π

Для ε £ 1 нельзя найти единого δ

> 0 для всех точек изç

ú .

Однако, если функция непрерывна на отрезке, то ситуация меняется.

Теорема Кантора. Если функция непрерывна на отрезке, то она равномерно

непрерывна на этом отрезке.

Доказательство (от противного).

Пусть функция f(x) не является равномерно непрерывной на [a, b]. Тогда

$ ε 0 > 0 " δ > 0 $ x1 Î [a,b], $ x2 Î [a,b]

x1 - x2

< δ Þ

f ( x1 ) - f ( x2 )

³ ε 0 .

При каждом n N возьмем δ

. Тогда

< 1

f (x(n) )- f (x(n) )

$ x(n)

Î [a,b], $ x(n)

Î [a,b]:

x(n) - x(n)

³ ε

0 .

{x( n) } можно

По теореме Больцано-Вейерштрасса, из ограниченной последовательности

выделить сходящуюся к некоторой точке x0 Î [a, b] подпоследовательность.

Чтобы не усложнять обозначений, будем считать, что уже сама последовательность x1(n) ® x0 .

Тогда x2(n) ® x0 , т.к.	x1( n)	- x2( n)	<	1	. Поскольку функция непрерывна в точке x0, то

				n
f (x1( n) ) ® f ( x0 ) при n →					f (x2( n) ) ® f ( x0 ) .
		∞ , тогда

Отсюда

f (x( n) ) - f (x( n) )

® 0

, а это противоречит тому, что

f (x( n) ) - f (x( n) )

³ ε

. Значит,

предположение неверно, и функция равномерно непрерывна на отрезке [a, b]. ■

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2512 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке 15-10-2013_17-20-24

#
27.03.201529.7 Кб32Коллоквиум1.doc
#
27.03.20152.72 Mб151Мои лекции по матем анализу 1 часть.pdf