§ 4.4. Другий закон термодинаміки. Енергія гіббса

Перший закон термодинаміки за своєю суттю є законом збереження. Він дозволяє розраховувати енергетику процесу, однак не вирішує питання про можливість перебігу процесу та його напрямленість . Наприклад, такі нереальні явища, як самочинне стиснення газу чи перехід тепла від холодного тіла до гарячого, не суперечать першому закону термодинаміки.

З досвіду відомо, що самочинно всі процеси проходять з певною спрямованістю, наприклад, самовільно газ поширюється на весь об’єм(Рис. 7).

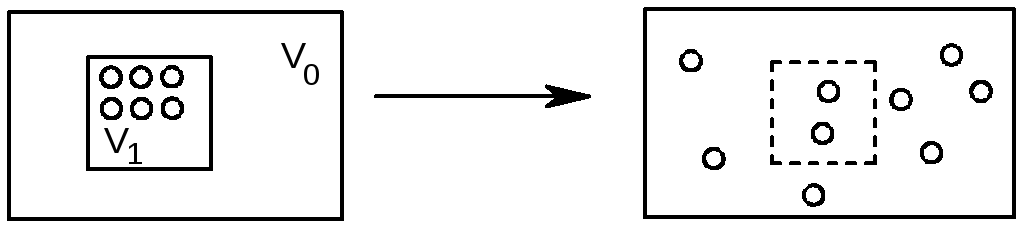
Рис. 7

Cамовільно теплота може переходити від гарячого тіла (Т₂) з більшою енергією до холодного (Т₁) з меншою енергією до рівноважного стану (Т

₁=Т₂=Т_сер). (Рис. 8).

Рис. 8

Відповідь на питання про можливість перебігу процесу та його напрямок дає другий закон термодинаміки. У підручниках для другого принципу термодинаміки звичайно наводиться безліч формулювань, наприклад:

«Теплота не може самовільно передаватися від більш холодного тіла до більш гарячого» (Клаузіус).

«Теплота найбільш холодного з тіл, що беруть участь у процесі, не може служити джерелом роботи» (Томсон).

«Коефіцієнт корисної дії парової машини завжди менше одиниці» та ін.

Але вони у здебільшого важливі для фізичних процесів. А для хімічних важливо те, що другий принцип термодинаміки дає критерії того, які процеси можуть проходити самовільно, а які не можуть.

Для характеристики більш імовірних процесів у термодинаміці використовують поняття – термодинамічна імовірність, W.

Термодинамічна імовірність W – це кількість мікростанів системи, якими реалізується макростан системи.

Мікростан системи – це таке розташування окремих частинок (молекул) у даний момент часу, що відповідає найбільш стійкому стану системи.

Отже, як критерій можливості перебігу процесу можна використовувати W - термодинамічну імовірність. Вона є функцією стану і максимальна при рівновазі. ОднакWзв'язана з механічними характеристиками системи: швидкістю руху молекул, їх положенням у просторі і т. д. А для хімічної термодинаміки важливо знайти критерій напрямку процесу, обумовлений термодинамічними параметрами:Т, Р, V(температура, тиск, об’єм).

Другий принцип термодинаміки вводить у розгляд новий критерій – ентропію S, що служить мірою енергетичного безладдя в системі.Ентропія зв'язана з термодинамічною імовірністю співвідношенням: S= k^.lnW, де k=R/N_A 1,381^.10^-23Дж/град– це константа Больцмана, має розмірність енергії, віднесеної до температури і одній частці. Отже, з її допомогою здійснюється перехід від просто «безладдя» системи до «енергетичного безладдя». У розрахунку на 1 моль часток: S=R^.lnW.

Зміна ентропії (S) в процесі визначається зміною числа мікростанів системиS = S₂ – S₁ = R^.ln W₂/W₁.

Досвід показує, що більшість самовільних процесів проходять з виділенням теплоти (Н0). Але серед них зустрічаються також ендотермічні(Н0). Прикладом є розчинення амонію нітрату у воді:

NH₄NO_{3 (Т)}  NH₄NO_{3 (Р)}; Н⁰_х.р. = + 27 кДж/моль.

Виходить, тепловиділення не є вирішальним критерієм можливості самовільного перебігу процесів.

Так само можуть самовільно проходити процеси зі зменшенням ентропії (S0): С_(Т) + О_2(Г)  СО_2(Г).Між молекулами карбонуСі киснюО₂встановлюється зв'язок, і тому ступінь енергетичного безладдя зменшується.

Який же критерій самовільності – ентальпія(Н)чи ентропія(S)?

Критерієм, що визначає можливість перебігу процесу, є баланс дії ентальпії (Н) і ентропії (S). Тому можливі самовільні процеси з поглинанням теплоти (якщо ріст енергетичного «безладдя» є більш вагомим), і процесиз S0 (якщо це супроводжується більш сильним виділенням теплоти).

Вимірюється зміна ентропії приведеною теплотою оборотногопроцесу, що зв'язує відповідні стани системи:

S = Q_обор./Т.

Для необоротнихпроцесів:S  Q_{необор.}/Т(алгебраїчна сума приведених теплот для необоротних процесів:Q_{необор.проц.}  Q_{обор .проц.}

Математичне формулювання II закону термодинаміки (узагальнена формула) виглядає таким чином:

S  Q/T

Для ізольованих систем, де обмін енергією з навколишнім середовищем виключений,Q=0,другий принцип термодинаміки виглядає:S 0.

Таким чином, для ізольованих систем залишається тільки один критерій самовільного перебігу процесів – збільшення ентропії. Самовільними є лише процеси, що ведуть до збільшення загальної ентропії. Отже:

1.Ентропія – це функція стану системи, тому обчислювати зміну ентропії можна аналогічно наслідку із закону Гесса. Ентропія хімічної реакції дорівнює різниці між сумами ентропій продуктів реакції ( S_прод)і ентропій вихідних речовин ( S_вих.р),з урахуванням стехіометричних коефіцієнтів.

S_х.р. =  S_прод. -  S_вих.р., з урахуванням стехіометричних коефіцієнтів.

Задача.Розрахувати зміну ентропії хімічних реакцій(S_х.р.) для процесу:3С₂Н_2(Г)  С₆Н_{6 (Р).}

Розв’язок.

S_х.р. = S⁰ (C₆H_{6 (Р)}) – 3 S⁰ (С₂Н_{2 (Г)}).

S_х.р. = 269,2 – 3 ^. 200,8 = - 333,2 Дж/моль^.К.

2.Ентропія виміряється приведеною теплотою.

Задача.Чому дорівнює збільшення ентропії моляFeприТ_пл=1536⁰С (1809К) при переході з кристалічного в рідкий стан, якщо ентальпіяН_пл= 13765Дж/моль.

Розв’язок.

При температурі плавлення Fe_кр  Fe_р( у рівновазі

T=const = Т_пл.).

S_пл = S (Fe (р)) -S (Fe (_T)) =Н_пл/Т_пл= 13765/1809= 7,61 Дж/ моль^.К.

S0  процес при Т_пл відбувається самовільно.

3. Ентропія є критерієм самовільного перебігу процесів тільки для ізольованих систем. Самовільно проходять в ізольованих системах тільки ті процеси, що йдуть зі збільшенням ентропії.

Рис. 9

4. Sзв'язана з числом можливих мікростанів у системі (тобто з термодинамічною імовірністюW), характеризує міру енергетичного безладдяS= klnWу системі.

5. S – це термодинамічна функція, що на відміну від термодинамічної імовірностіWзв'язана з термодинамічними величинамиQ;T, тобто більш прийнятна для хімічної термодинаміки.

Однак у природних процесах і в техніці частіше зустрічаються системи, що взаємодіють з навколишнім середовищем, тобто неізольовані. Ентропія S мало підходить для характеристики процесів у цих умовах.

Для ізохорно-ізотермічнихумов перший закон термодинаміки має таку математичну форму запису:Q_V = U (A= РV; V= const  A=0).

З II -го закону термодинаміки випливає: S  Q_V /T  Q_V  ТS.

Поєднуючи дві математичні форми запису, одержимо: TS  U;

U - TS  0.

Позначимо різницю U - TSчерез нову термодинамічну функцію стану –вільну енергію Гельмгольца, U - TS =F.

Отже, II закон термодинаміки стосовно ізохорно-ізотермичних процесівможна записати так: F 0.

Введення даної функції дозволяє користатися лише одним критерієм напрямку процесу (який для ізольованих систем є S). Однак цей чисто формальний прийом не скасовує того факту, що насправді для самовільних процесів залишаються ті ж критерії: НіS.ЧерезFпозначений їхній баланс.

Отже:1. Для ізохорно-ізотермічних умов Fє сумарним критерієм самовільного перебігу процесів

F=U - TS (це вираження об'єднаних I і II законів термодинаміки).

2. Самовільними є такі процеси для ізохорно- ізотермічних умов, у яких енергія Гельмгольца зменшується (F 0).

Стан рівноваги

Закриті системи за постійних V і T

F 0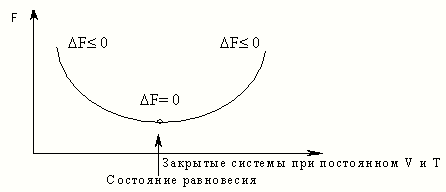

Рис. 10

F0,процеси можуть йти самовільно;

F= 0,процеси займають прикордонне положення, що

характеризується мінімальним значенням F;

F  0, процеси у прямому напрямку самостійно проходити не

можуть.

3.Енергія Гельмгольца є функцією стану системи, тому обчислити зміну енергії Гельмгольца можна також використовуя наслідок із закону Гесса.

Енергія Гельмгольца хімічної реакції дорівнює різниці між сумами енергій Гельмгольца продуктів реакції (F⁰_f,прод) і енергій Гельмгольца вихідних речовин (F⁰_f,вих.р) з урахуванням стехіометричних коефіцієнтів.

F_х.р. = F⁰_f,прод. - F⁰_f,вих.р, з урахуванням стехіометричних коефіцієнтів.

Для ізобарно-ізотермічних умов I-й закон термодинаміки можна записати у вигляді:Q_P = U + РV; тобто теплота при ізобарно-ізотермічних умовах дорівнює зміні ентальпіїQ_P = U + pV = H(за умови, що не відбувається ніякої іншої роботи, як проти тиску). ПоєднуючиS  Q_P/T-вираження II закону термодинаміки, одержимо:Н - ТS 0.Якщо вираженняН - ТSпозначити через нову термодинамічну функцію стану –вільну енергію Гіббса, G :

Н - ТS = G,

отже, II -ий принцип термодинаміки, стосовно ізобарно-ізотермічних процесів можна записати так: G 0. G – енергія Гіббса, так само як і енергія Гельмгольца, є лише балансом усіх тих же двох критеріїв самовільного перебігу процесів: виділення теплоти і зростання ентропії. Отже:

1. Для ізобарно-ізотермічних умов Gє сумарним критерієм самовільного перебігу процесівG = Н - ТS( об'єднаний ( I і II ) закон термодинаміки).

2.Процеси, у яких:

 G  0, можуть йти самовільно;

G = 0, займають прикордонне (рівноважне) положення;

G  0, самочинний перебіг процесів у прямому напрямку неможлив.

Закриті системи за постійних Т і Р

Стан рівноваги

G  0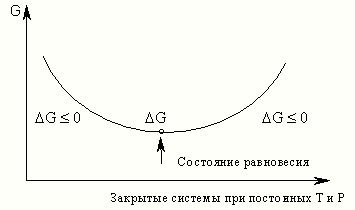

Рис. 11

3. Gє функцією стану системи, тому обчислити зміну енергії Гіббса хімічних реакцій можна аналогічно наслідку із закона Гесса.

Енергія Гіббса хімічних реакцій дорівнює різниці між сумами енергій Гіббса продуктів реакції (G⁰_{f,298 прод.}) і енергій Гіббса вихідних речовин ( G⁰_{f,298 вих.р.}) з урахуванням стехіометричних коефіцієнтів.

G_х.р= G⁰_{f,298 прод.} -  G⁰_{f,298 вих.р.},з урахуванням стехіометричних коефіцієнтів;

G⁰_f,298(Х)– стандартна енергія Гіббса речовиниХза стандартних умов і у певному агрегатному стані.

Для простих речовин і елементів G⁰_f,298(Х) як і Н⁰_f,298(Х))дорівнюють нулю.

Задача:спиртове шумування відбувається за рівнянням реакції:

С₆Н₁₂О_6(Р)  2С₂Н₅(ОН) _(Р) + 2СО_2(Г)

G⁰_f,298, кДж/моль -915 -174 -394.

Розв’язок.

G⁰_х.р. = 2(-174) + 2(-394) – (-915)= -221 кДж/моль.

Н⁰_х.р. цього процесу становить – 79 кДж/моль. Отже, за рахунок ентропійного внеску здатність шумування робити корисну роботу збільшується майже втроє. Це дуже важливо, тому що подібні процеси є найважливішим джерелом енергії як у багатьох так званих анаеробних організмів, так і у тварин і людини за інтенсивного м'язового навантаження.

4. Функція Gназивається енергією, тому що визначаєпрацездатністьвідповідного процесу. А самеG чисельно дорівнює корисній максимальній роботі, що могла б бути зроблена в ході ізобарно-ізотермічного процесу (дивись с.82).

Питання для самоконтролю

1. Як визначається термодинамічна імовірність?

2. Що за функція стану – ентропія?

3. Сформулюйте II закон термодинаміки.

4. Який має вираз II закон термодинаміки для ізобарних хімічних процесів?

5. Що визначають за зміною енергії Гіббса?

6.За допомогою якого критерію можно стверджувати про можливість

перебігу реакцій в ізольованих системах ?

7.Як можно порахувати зміну ентропії реакції?

8.Як можно порахувати зміну енергії Гіббса реакції?

Р о з д і л 5

ХІМІЧНА КІНЕТИКА