algebra10_нелін_дворівн

§ 5. Графіки функцій синуса, косинуса, тангенса і котангенса та їх властивості

Приклад 2 Розташуйте в порядку зростання числа: sin 1,9; sin 3; sin (–1); sin (–1,5).

К о м е н т а р Для розміщення заданих чисел у порядку їх зростання з’ясуємо, які з них

додатні, а які від’ємні, а потім порівняємо між собою окремо додатні числа і окремо від’ємні, користуючись відомими проміжками зростання і спадання функції sin х.

Р о з в ’ я з а н н я

XЧисла sin 1,9 і sin 3 — додатні (точки Р1,9 і Р3 знаходяться в ІІ чверті), а числа sin (–1) і sin (–1,5) — від’ємні (Р–1 і Р–1,5 знаходяться в ІV чверті).

2π; π спадає, з нерівності 1,9 < 3 одержуємо sin 1,9 > sin 3.

тає. Враховуючи, що –1 > –1,5, одержуємо sin (–1) > sin (–1,5). Отже, у порядку зростання ці числа розташовуються так:

sin (–1,5); sin (–1); sin 3; sin 1,9. Y

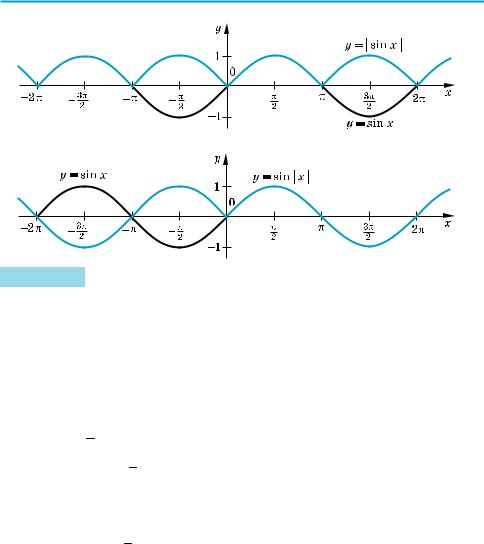
Приклад 3 Побудуйте графік функції: 1) у = | sin х |; 2) у = sin | х |.

К о м е н т а р Графіки заданих функцій можна одержати за допомогою геометричних

перетворень графіка функції f (x) = sin х. Згадаємо відповідні перетворення:

1)у = | sin х | = | f (x) | — вище осі Ox (і на самій осі) графік y = sin x залишаєть ся без зміни, нижче осі Ox — симетрично відображується відносно осі Ox;

2)у = sin | х | = f (| x |) — праворуч від осі Oy (і на самій осі) графік y = sin x — без зміни, і та сама частина графіка симетрично відображується відносно осі Oy.

Р о з в ’ я з а н н я

X Побудуємо спочатку графік функції у = f (x) = sin х:

71

РОЗДІЛ 1. Тригонометричні функції

1) у = | sin х | = | f (x) |

Y

2) у = sin | х | = f (| x |)

Y

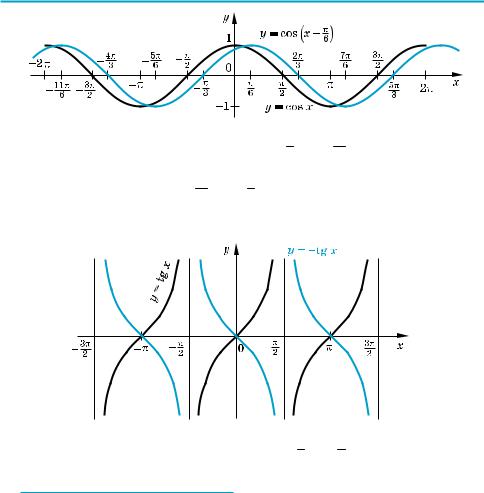
Приклад 4 Побудуйте графік функції та вкажіть проміжки її спадання

К о м е н т а р Графіки заданих функцій можна одержати за допомогою геометричних

перетворень графіків функцій:

1)f (x) = cos х;

2)ϕ (x) = tg х. Тоді одержуємо:

1) y = cos(x − 6π )= f(x − 6π ) — паралельним перенесенням графіка функції f (x) уздовж осі Ох на 6π одиниць;

2)y = –tg х = –ϕ (x) — симетрією графіка функції ϕ (x) відносно осі Ох.

Щоб записати проміжки спадання і зростання функцій, відмітимо, що

функція y = cos(x − 6π ) періодична з періодом T = 2π, а функція у = –tg х періо

дична з періодом T = π. Тому для кожної функції досить з’ясувати на одному періоді, де вона спадає і де зростає, а потім одержані проміжки повторити через період.

Р о з в ’ я з а н н я

72

§ 5. Графіки функцій синуса, косинуса, тангенса і котангенса та їх властивості

Функція спадає на кожному з проміжків 6π +2πk; 76π +2πk , k Z, і зростає

на кожному з проміжків −56π +2πk; 6π +2πk , k Z. Y

2)X Графік функції у = –tg х одержуємо симетричним відображенням графіка функції у = tg х відносно осі Ох.

Функція спадає на кожному з проміжків (− 2π + πk; 2π + πk), k Z. Y

Запитання для контролю

1.а) Побудуйте графік функції у = sin х. Користуючись графіком, охаракте ризуйте властивості цієї функці.

б*) Обґрунтуйте властивості функції у = sin х.

2.а) Побудуйте графік функції у = cos х. Користуючись графіком, охаракте ризуйте властивості цієї функції.

б*) Обґрунтуйте властивості функції у = cos х.

3.а) Побудуйте графік функції y = tg х. Користуючись графіком, охаракте ризуйте властивості цієї функції.

б*) Обґрунтуйте властивості функції y = tg х.

4.а) Побудуйте графік функції y = ctg х. Користуючись графіком, охаракте ризуйте властивості цієї функції.

б*) Обґрунтуйте властивості функції у = ctg х.

73

РОЗДІЛ 1. Тригонометричні функції

74

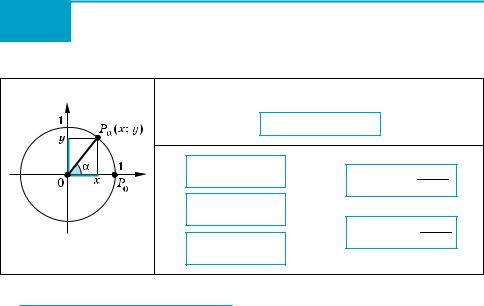
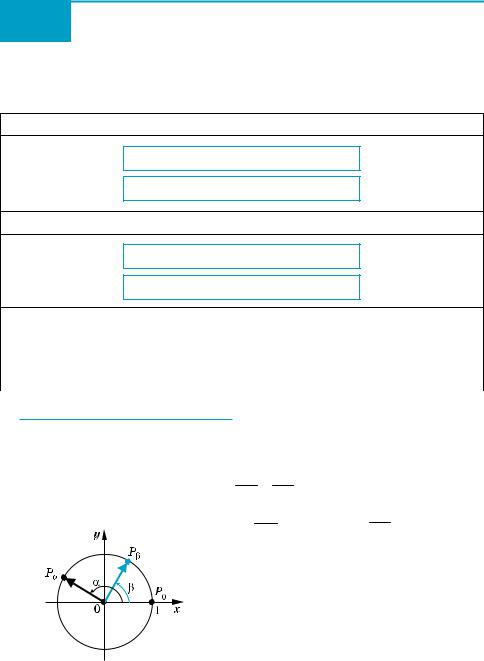
( На рисунку в таблиці 14 зображене одиничне коло, тобто коло радіуса 1 з центром в початку координат. Рівняння цього кола: x2 + y2 = 1.

Нехай при повороті на кут α точка P0 (1; 0) одиничного кола переходить у точку Pα (x; y) (тобто при повороті на кут α радіус OP0 переходить у радіус OPα). Нагадаємо, що синусом α називається ордината точки Pα (x; y) одинич ного кола, тобто sin α = y, а косинусом α називається абсциса цієї точки, тобто cos α = x. Координати точки Pα задовольняють рівнянню кола, тоді y2 + x2 = 1, отже,

sin2 α + соs2 α = 1. )

Це співвідношення називають основною тригонометричною тотожністю. Нагадаємо також, що:

tg αæ ctg α = 1 (sin α ≠ 0 і cos α ≠ 0).

За допомогою цих співвідношень і основної тригонометричної тотожності одержуємо:

75

РОЗДІЛ 1. Тригонометричні функції

Приклади розв’язання завдань

Приклад 1 Знаючи значення однієї з тригонометричних функцій та інтер вал, у якому знаходиться α, знайдіть значення інших трьох тригонометричних функцій:

76

§ 6. Співвідношення між тригонометричними функціями одного аргументу

визначити знак, який потрібно взяти в правій частині формули (це знак косинуса в ІІІ чверті).

Для знаходження sin a можна ско ристатися співвідношенням

Приклад 3 Спростіть вираз sin4 α – соs4 α + соs2 α.

К о м е н т а р

Для перетворення тригонометричних виразів поряд з тригонометричними формулами використовують також алгебраїчні формули і, зокрема, формули скороченого множення. Так, вираз sin4 α – соs4 α можна розглядати як різни цю квадратів: (sin2 α)2 – (соs2 α)2. Тоді його можна розкласти на множники (як добуток суми і різниці sin2 α та соs2 α), а після цього вже використати основну тригонометричну тотожність: sin2 α + соs2 α = 1.

Р о з в ’ я з а н н я

Xsin4 α – соs4 α + соs2 α = (sin2 α + соs2 α)(sin2 α – соs2 α) + соs2 α = =1æ(sin2 α – соs2 α) + соs2 α = sin2 α – соs2 α +соs2 α = sin2 α. Y

К о м е н т а р

Спочатку використаємо означення тангенса і котангенса: tg α = sinα ,

cos α

ctg α = cos α , а після перетворення знаменника дробу — основну тригономет

sinα

77

РОЗДІЛ 1. Тригонометричні функції

ричну тотожність: sin2 α + соs2 α = 1, далі спрощуємо одержаний дріб. У кінці враховуємо, що a2 = a . Для розкриття знаку модуля знаходимо знак коси нуса в заданому проміжку і враховуємо, що при a < 0 значення | a | = –a.

Р о з в ’ я з а н н я

К о м е н т а р Доведемо, що ліва частина рівності дорівнює правій. Для цього в знамен

нику використаємо формулу tgα = sinα , а в чисельнику піднесемо вираз у дуж

cos α

ках до квадрата і використаємо формулу sin2 α + соs2 α = 1. Нагадаємо, що

тотожністю називається рівність, правильна при всіх допустимих значен( нях букв, які входять до неї. Тому задана рівність є тотожністю тільки за умови tg α ≠ 0 і соs α ≠ 0.

Р о з в ’ я з а н н я

2 = 2. Отже, задана рівність є тотожністю. Y

З а у в а ж е н н я. При доведенні тотожностей найчастіше використовують такі прийоми:

1)за допомогою тотожних перетворень доводять, що одна частина рівності дорівнює іншій;

2)розглядають різницю лівої і правої частин тотожності і доводять, що ця різниця дорівнює нулю (цей прийом використовують у тих випадках, коли планується перетворювати обидві частини тотожності).

Запитання для контролю

1.Запишіть співвідношення між тригонометричними функціями одного ар гументу.

2*. Доведіть співвідношення між тригонометричними функціями одного ар гументу.

78

§7 ФОРМУЛИ ДОДАВАННЯ ТА ЇХ НАСЛІДКИ

7.1. ФОРМУЛИ ДОДАВАННЯ

Т а б л и ц я 15

1. Косинус різниці і суми

cos (α – β) = cos α cos β + sin α sin β

cos (α + β) = cos α cos β – sin α sin β

2. Синус суми і різниці

sin (α + β) = sin α cos β + cos α sin β

sin (α – β) = sin α cos β – cos α sin β

3. Тангенс суми і різниці

Пояснення й обґрунтування

1. Косинус різниці і суми.

(Щоб одержати формулу для cos (α – β), спочатку розглянемо випадок, коли α і β знаходяться в проміжку [0; π] і α > β. На одиничному колі позначимо

точки Рα і Рβ та зобразимо вектори OPα і OPβ (рис. 71). Ці вектори мають ті

самі координати, що й точки Рα і Рβ, тобто:

OPα (cos α; sin α ), OPβ (cos β; sin β ). Довжини (модулі) цих векторів до$

80