
algebra10_нелін_дворівн
.pdf
§ 1. Повторення і розширення відомостей про функцію
Наприклад, якщо x3 > 8, тобто x3 > 23, то, враховуючи зростання функції f (x) = x3, одержуємо x > 2.
4. Парні і непарні функції. Розглянемо функції, області визначення яких симетричні відносно початку координат, тобто разом з кожним числом x містять і число (–x). Для таких функцій визначені поняття парності і непар ності.
Функція f називається парною, якщо для будь!якого x з її області визна! чення f (–x) = f (x).
Наприклад, функція y = x2 (тобто функція f (x) = x2) — парна, оскільки f (–x) = (–x)2 = x2 = f (x).
(Якщо функція f (x) парна, то до її графіка разом з кожною точкою M з ко
ординатами (x; y) = (x; f (x)) входить також і точка M1 з координатами (–x; y) = (–x; f (–x)) = (–x; f (x)). Точки M і M1 розміщені симетрично віднос но осі Oy (рис. 10), тому і весь графік парної функції розміщений симет! рично відносно осі Oy. )
Наприклад, графік парної функції y = x2 (рис. 9) симетричний відносно осі Oy.
Функція f називається непарною, якщо для будь!якого x з її області ви! значення f (–x) = –f (x).
Наприклад, функція y = x1 (тобто функція f(x) = x1 ) — непарна, оскільки
f(−x) = 1 = − 1 = −f(x) .
−x x
(Якщо функція f (x) непарна, то до її графіка разом з кожною точкою M
з координатами (x; y) = (x; f (x)) входить також і точка M1 з координатами (–x; y) = (–x; f (–x)) = (–x; –f (x)). Точки M і M1 розміщені симетрично відносно початку координат (рис. 11), тому і весь графік непарної функції розміщений симетрично відносно початку координат. )
Наприклад, графік непарної функції y = x1 (див. пункт 4 табл. 1) симет ричний відносно початку координат, тобто відносно точки О.
Рис. 9 |
Рис. 10 |
Рис. 11 |
11

РОЗДІЛ 1. Тригонометричні функції
Приклади розв’язання завдань
Приклад 1 Знайдіть область визначення функції:
1) y = x2 + x; 2) |
y = |
|
x |
; 3) |
y = x + 5 . |
|
x2 |
+ x |
|||||
|
|
|
|
Ро з в ’ я з а н н я
1)XОбмежень для знаходження зна
чень виразу x2 + x немає, отже, D (y) = R.Y
2)X Область визначення функції
y = x задається обмеженням x2 + x
x2 + x ≠ 0, оскільки знаменник дробу не може дорівнювати нулю. З’ясуємо, коли x2 + x = 0. Маємо х(x + 1) = 0, x = 0 або x = –1. Тоді область визначення можна задати обмеженнями x ≠ 0, x ≠ –1,
або записати так:
D (y) = (– ; –1) (–1; 0 ) (0; + ).Y
3)X Область визначення функції
y = x + 5 задається обмеженням
x + 5 0, тобто x –5, оскільки під знаком квадратного кореня по винен стояти невід’ємний вираз.
Отже, D (y) = [– 5; + ).Y
К о м е н т а р
Оскільки всі функції задано фор мулами, то їх області визначення — це множина всіх значень змінної х, при яких формула має зміст, тобто має зміст вираз, який стоїть у правій частині формули у = f (x).
У курсі алгебри зустрічалися тіль ки два обмеження, які необхідно вра ховувати при знаходженні області визначення:
1)якщо вираз записано у вигляді дро( бу BA , то знаменник B ≠ 0;
2)якщо запис виразу містить квад(
ратний корінь A , то підкорене( вий вираз A 0.
У всіх інших випадках, які вам доводилося розглядати, областю ви значення виразу були всі дійсні чис ла*.
Приклад 2* Знайдіть область значень функції y = x2 – 3.
|
Р о з в ’ я з а н н я |
К о м е н т а р |
XСкладаємо рівняння х2 – 3 = а. Воно |
Позначимо значення заданої |
|
рівносильне рівнянню х2 = а + 3, яке |
функції f (x) (тобто х2 – 3) через a і з’я |
|
має розв’язки, якщо а + 3 0, тобто |
суємо, для яких a можна знайти від |
|
при а –3. Усі ці числа і складуть об |
повідне значення x (при цьому зна |
|
ласть значень функції. |
ченні x значення f (x) = a). |
|
Отже, область значень заданої |
Тоді всі числа a, для яких існує |
|
функції |
хоча б один корінь рівняння f (x) = a, |
|
E (f) = [–3; + ) (тобто у –3).Y |
ввійдуть до області значень функції |
|
|
|
f (x). Множина всіх таких а і складе |
|
|
область значень функції. |
|
|
|
*У подальшому курсі алгебри і початків аналізу 10 класу з’являться нові вирази
зобмеженнями: tg α, ctg α, arcsin a, arccos a, logAB, n a , aα, де α — не ціле число.
12

§ 1. Повторення і розширення відомостей про функцію
Корисно пам’ятати, що
область значень функції у = f (x) збігається з множиною тих зна! чень а, при яких рівняння f (x) = а має розв’язки.
Приклад 3* Доведіть, що при k ≠ 0 областю значень лінійної функції y = kx + b є множина всіх дійсних чисел.
Р о з в ’ я з а н н я
XЯкщо kx + b = a (де k ≠ 0), то розв’я
зок цього рівняння x = a − b існує для k
будь якого a R (k ≠ 0 за умовою). Таким чином, значенням заданої
функції може бути будь яке дійсне число, отже, її область значень
E (f) = R.Y
К о м е н т а р
Позначимо значення заданої функції f (x) (тобто kx + b) через a
із’ясуємо, для яких a можна знайти відповідне значення x, таке, що f (x) = a.
Множина всіх таких значень a
ібуде складати область значень функ ції f (x).
Приклад 4* Доведіть, що лінійна функція y = kx + b при k > 0 є зростаю!
чою, а при k < 0 — спадною.
Р о з в ’ я з а н н я
X Нехай x2 > x1 (тоді x2 – x1 > 0). Роз глянемо різницю f (x2) – f (x1) =
=kx2 + b – (kx1 + b) = k(x2 – x1). Оскільки x2 – x1 > 0, то при k > 0
маємо f (x2) – f (x1) > 0, отже,
f (x2) > f (x1) — функція зростає. При k < 0 маємо f (x2) – f (x1) < 0,
отже, f (x2) < f (x1) — функція спа дає. Y
Приклад 5* Доведіть, що:
К о м е н т а р
Для обґрунтування зростання або спадання функції корисно пам’ятати, що для доведення нерівності
f (x2) > f (x1) чи f (x2) < f (x1) досить знайти знак різниці f (x2) – f (x1).
Нам задано функцію f (x) = kx + b. Ця функція буде зростаючою, якщо з нерівності x2 > x1 буде випливати нерівність f (x2) > f (x1), а для дове дення останньої нерівності досить знайти знак різниці f (x2) – f (x1) (ана логічно обґрунтовується і спадання функції).
1)сума двох зростаючих на множині Р функцій завжди є зро! стаючою функцією на цій множині;
2)сума двох спадних на множині Р функцій завжди є спад! ною функцією на цій множині.
Р о з в ’ я з а н н я |
К о м е н т а р |
1) XНехай функції f (x) і g (x) є зрос |
Для доведення зростання суми |
таючими на одній і тій самій мно |
двох зростаючих функцій f (x) і g (x) |
|
|
13

РОЗДІЛ 1. Тригонометричні функції
жині Р. Якщо x2 > x1, то
f (x2) > f (x1) і g (x2) > g (x1). Додаючи почленно останні нерів
ності, одержуємо
f (x2) + g (x2) > f (x1) + g (x1). Це і означає, що сума функцій f (x)
і g (x) є зростаючою функцією на множині Р.Y
2)XНехай функції f (x) і g (x) є спад ними на множині Р. Тоді з нерів
ності x2 > x1 маємо f (x2) < f (x1) і g (x2) < g (x1).
Після почленного додавання ос танніх нерівностей одержуємо:
f(x2) + g (x2) < f (x1) + g (x1),
аце й означає, що сума функцій
f (x) і g (x) є спадною функцією на множині Р.Y
досить довести, що на множині Р з не рівності x2 > x1 випливає нерівність
f (x2) + g (x2) > f (x1) + g (x1). Аналогічно для доведення того, що
сума двох спадних функцій є спадною функцією, достатньо довести:
якщо x2 > x1, то
f (x2) + g (x2) < f (x1) + g (x1).
Приклад 6 Доведіть, що зростаюча або спадна функція набуває кожного
свого значення тільки в одній точці її області визначення.
Д о в е д е н н я
XНехай функція f (x) є зростаючою і
f (x1) = f (x2). (1) Припустимо, що
x1 ≠ x2.
Якщо x1 ≠ x2 , то або x1 > x2, або x1< x2. Враховуючи зростання f (x),
у випадку x1 > x2 маємо f (x1) > f (x2), що суперечить рівності (1). У випадку
x1 < x2 маємо f (x1) < f (x2), що також суперечить рівності (1).
Отже, наше припущення непра вильне, і рівність f (x1) = f (x2) мож лива тільки при x1 = x2. Тобто зрос таюча функція набуває кожного сво го значення тільки в одній точці її об ласті визначення.
Аналогічно доводиться тверджен ня і для спадної функції. Y
К о м е н т а р
Доведемо це твердження методом від супротивного. Для цього досить припустити, що виконується проти лежне твердження (функція може набувати одного й того самого значен ня принаймні у двох точках), і одер жати суперечність. Це означатиме, що наше припущення неправильне, а правильне задане твердження.
14

§ 1. Повторення і розширення відомостей про функцію
Приклад 7 Дослідіть, які з заданих функцій є парними, які непарними, а які — ні парними, ні непарними:
1) |
y = |
1 |
; |
2) y = x4; 3) y = x3 + x. |
|
x + 1 |
|||||
|
|
|
|
Ро з в ’ я з а н н я
1)X Область визначення функції
y = |
1 |
: x ≠ –1, тобто вона не си |
|
x + 1 |
|||
|
|
метрична відносно точки О (точка x = 1 входить до області визначен ня, а x = –1 — ні).
Отже, задана функція не може бути ні парною, ні непарною.Y
2)X Область визначення функції y = x4: D (y) = R, тобто вона симет рична відносно точки О.
f (–x) = (–x)4 = x4 = f (x), значить, функція парна.Y
3)X Область визначення функції y = x3 + x: D (y) = R, значить, вона симетрична відносно точки О.
f (–x) = (–x)3 + (–x) = –x3 – x =
= –(x3 + x) = –f (x), отже, функція непарна.Y
К о м е н т а р
Для дослідження функції y = f (x) на парність чи непарність досить, по перше, упевнитися, що область ви значення цієї функції симетрична від носно точки О (разом з кожною точ кою x містить і точку –x) і, по друге, порівняти значення f (–x) і f (x).
Запитання для контролю
1.Що називається числовою функцією? Наведіть приклади таких функцій.
2.На прикладах поясніть, що таке область визначення функції та область значень функції. Які обмеження необхідно врахувати при знаходженні
області визначення функції y = |
x |
? Знайдіть її область визначення. |
|
x |
|||
|
|
3.Що називається графіком функції у = f (x)? Наведіть приклади.
4.Яка функція називається зростаючою? Наведіть приклади.
5.Яка функція називається спадною? Наведіть приклади.
6.Яка функція називається парною? Наведіть приклади. Як розміщено графік парної функції на координатній площині? Наведіть приклади.
7.Яка функція називається непарною? Наведіть приклади. Як розміщено графік непарної функції на координатній площині? Наведіть приклади.
15

РОЗДІЛ 1. Тригонометричні функції
Вправи
1°. Знайдіть значення функції у вказаних точках:
1)f (x) = x + x1 у точках 2; –1; 3; а (а ≠ 0);
2)g (x) = х2 – 3 у точках 0; 1; –2; b;
3)ϕ (x) = x + 1 у точках 0; 3; –1; m (m > 0).
2.Знайдіть область визначення функції, заданої формулою:
|
|
|
|
1 |
|
|
|
|
|
x |
|
|
|||
1°) у = 2х + 3; |
2°) y = |
x + 3 ; |
3°) y = |
|
|
|
; |
|
|
4) y = |
|
|
; |
|
|
x + 1 |
|
|
x2 + 1 |
||||||||||||
5) y = x2 −1 ; |
6) y = x2 + 1 ; |
7) y = x −1 + 5 − x ; 8) y = |
|
x + 3 |
; |
||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
9*) y = x2 − 9 ; |
10*) y = |
|
x2 − x |
; 11*) y = |
|
|
x |
|
; |
12*) y = x2 + x + 1 . |
|||||
|
x + 1 |
x |
|
− |
2 |
||||||||||
x − 3 |
|
|
|
|
|
|
|
|
|
|
|
||||
3. Знайдіть область значень функції, заданої формулою: |
|
|
|||||||||||||
1) f (x) = 5; |
2) f (x) = х; |
3) f (x) = х2; |
4) f (x) = x ; |
||||||||||||
5*) у = –3х + 1; |
6*) у = х2 – 5; |
7*) у = | х | + 3 . |
|
|
|
|
|
||||||||
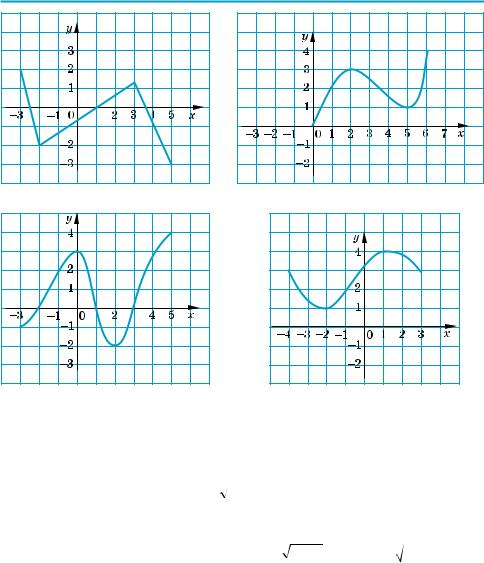
4°. Для функцій, які задані своїми графіками на рисунку 12, укажіть область визначення, область значень, проміжки зростання і спадання та значення кожної функції при х = 1.
5. Обґрунтуйте, що задана функція є зростаючою (на її області визначення):
1) у = 3х; |
2) у = х + 5; |
3*) у = х3; |
4*) у = х5; |
5*) y = x . |
|
6*. Доведіть, що на заданому проміжку функція зростає: |
|
||||
1) y = − 2 , де х > 0; |
2) |
y = − 1 , де х < 0. |
|
||
x |
|
|
x |
|
|
7. Обґрунтуйте, що задана функція є спадною (на її області визначення):
1) у = –3х; |
2) у = –х – 1; |
|
3*) у = –х3; |
4*) у = –х5. |
|
8*. Доведіть, що на заданому проміжку функція спадає: |
|
||||
1) y = 3 , де х < 0; |
2) y = |
5 |
, де х > 0. |
|
|
x |
|
|
x |
|
|
9*. Доведіть, що функція у = х2 на проміжку [0; + ) зростає, а на проміжку (– ; 0] спадає.
10*. Користуючись твердженнями, доведеними у прикладі 5 (с. 13), укажіть, які із заданих функцій є зростаючими, а які — спадними:
1) у = х3 + x; 2) у = –х – x5 ; 3) y = x + x ; |
4) у = –х3 – х5. |
16
§ 1. Повторення і розширення відомостей про функцію
а |
б |
в |
г |
|
Рис. 12 |
11*. Користуючись твердженнями, доведеними у прикладі 6 (с. 14): |
|
1)обґрунтуйте, що рівняння х3 + х = 10 має єдиний корінь х = 2;
2)підберіть корінь рівняння x + x = 6 і доведіть, що інших коренів це рівняння не має.
12.Обґрунтуйте, що задана функція є парною:
1) у = х6; |
2) y = |
1 |
+ 1; |
3) y = x2 + 1 ; |
4) y = |
|
x |
|
+ x4 . |
|||
|
|
|||||||||||
|
|
|||||||||||
|
|
x2 |
|
|
|
|
|
|
||||
13. Обґрунтуйте, що задана функція є непарною: |
|
|
|
|
|
|||||||
1) у = х5; |
2) y = − |
1 |
; |
3) у = х | х |; |
4) у = х3 – х . |
|||||||
x3 |
||||||||||||
17
|
|
РОЗДІЛ 1. Тригонометричні функції |
|
|
||||
1.2. ВЛАСТИВОСТІ І ГРАФІКИ ОСНОВНИХ ВИДІВ ФУНКЦІЙ |
|
|
||||||
|
|
|
|
|
|
|
Т а б л и ц я 2 |
|
|
|
|
|
|
|
|
|
|
Умови |
|
|
|
Властивості |
|
|
||
для |
Графік |
|
|
|
|
|
|
|
|
|
|
парність і |
|
зростання і |
|||
коефіці |
D (y) |
E (y) |
|
|
||||
|
|
|
|
|||||
єнтів |
|
|
|
непарність |
|
спадання |
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
1 |
2 |
|
3 |
4 |
|
5 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
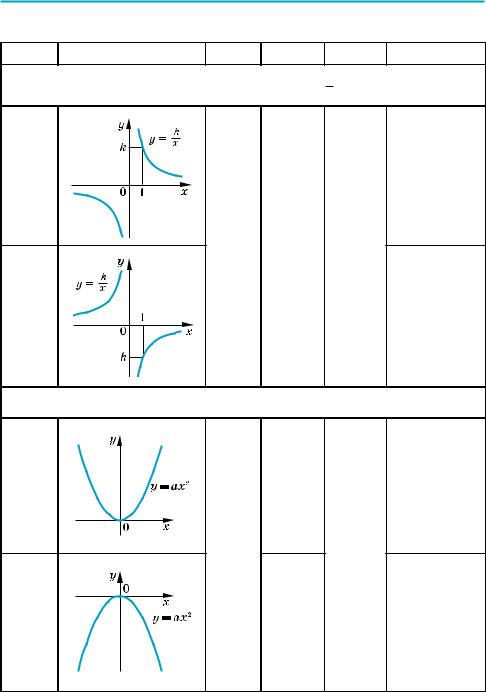
1. Лінійна функція y = kx + b |
|
|
|
|||
k > 0 |
зростає |
|
ні парна, ні непарна
k < 0 |
|
|
|
|
|
|
R |
|
спадає |
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
при k > 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зростає |
b = 0 |
|
|
|
|
|
|
|
|
|
y = kx |
|
|
|
|
|
|
|
непарна |
|
|
|
|
|
|
|
|
при k < 0 |
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
спадає |
|
|
|
|
|
|
|
|
|
|
k = 0 |
|
|
|
b |
парна постійна |
y = b |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18
|
§ 1. Повторення і розширення відомостей про функцію |
|
||||
|
|
|
|
|
П р о д о в ж. т а б л. 2 |
|
1 |
2 |
3 |
4 |
|
5 |
6 |
|
2. Обернена пропорційність, функція y = k |
(k ≠ 0) |
|
|||
|
|
|
|
x |
|
|
|
|
|
|
|
|
спадає на |
|
|
|
|
|
|
кожному з |
k > 0 |
|
|
|
|
|
проміжків |
|
|
|
|
|
|
(– ; 0) |
|
|
|
|
|
|
i (0; + ) |
|
|
x 0 |
y 0 |
непарна |
|
|
|
|
|
|
|
|
зростає на |
|
|
|
|
|
|
кожному з |
k < 0 |
|
|
|
|
|
проміжків |
|
|
|
|
|
|
(– ; 0) |
|
|
|
|
|
|
i (0; + ) |
|
|
3. Функція y = ax2 (a 0 ) |
|
|
||
|
|
|
|
|
|
спадає на |
|
|
|
|
|
|
проміжку |
a > 0 |
|
|
[0; + ) |
|
|
(– ; 0], |
|
|
|
|
зростає на |
||
|
|
|
|
|
|
проміжку |
|
|
|
|
|
|
[0; + ) |
|
|
R |
|
|
парна |
|
|
|
|
|
|
|
зростає на |
|
|
|
|
|
|
проміжку |
a < 0 |
|
|
(– ; 0] |
|
|
(– ; 0], |
|
|
|
|
спадає на |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
проміжку |
|
|
|
|
|
|
[0; + ) |
|
|
19 |
|
|
|
|
РОЗДІЛ 1. Тригонометричні функції
П р о д о в ж. т а б л. 2
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
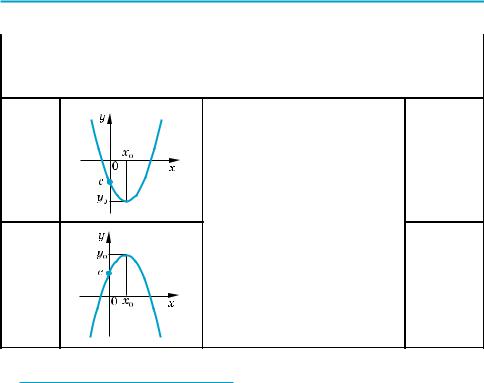
4. Kвадратична функція y = ax2 + bx + c (a ≠ 0, x0 |
= − |
b |
) |
|
2a |
||||
|
|
|
a > 0
a < 0
|
[y0; + ) |
у загально |
|
му виді — |
|
|
|
ні парна, ні |
|
|
непарна |
R |
|
при b = 0 |
|
||
|
|
|
|
|
функція |
|
(– ; y0] |
y =ax2 + c |
|
|
парна |
|
|
|
спадає на проміжку
(– ; x0], зростає на
проміжку [x0; + )
зростає на проміжку
(– ; x0], спадає на
проміжку [x0; + )
Пояснення й обґрунтування
1. Лінійна функція y = kx + b. Лінійною функцією називається функція виду y = kx + b, де k і b — деякі числа.
Обґрунтуємо основні характеристики цієї функції: область визначення, область значень, парність чи непарність, зростання і спадання.
Область визначення — множина всіх дійсних чисел: D (y) = R, оскільки формула kx + b має зміст при всіх дійсних значеннях x (тобто для будь якого дійсного x ми можемо обчислити значення kx + b).
Область значень лінійної функції буде різною залежно від значення кое фіцієнта k.
Якщо k = 0, то функція має вид y = b, тобто її область значень складається з одного числа b. У такому випадку графіком лінійної функції y = b є пряма, паралельна осі Ox, яка перетинає вісь Oy у точці b (рис. 13).
Якщо k ≠ 0, то E (y) = R (обґрунтування наведено в прикладі 3 на с. 13).
Парність і непарність лінійної функції суттєво залежить від значень ко ефіцієнтів b i k.
При b = 0 і k ≠ 0 функція y = kx + b перетворюється на функцію y = kx, яка непарна, оскільки для всіх x з її області визначення
f (–x) = k(–x) = –kx = –f (x).
20
