algebra10_нелін_дворівн

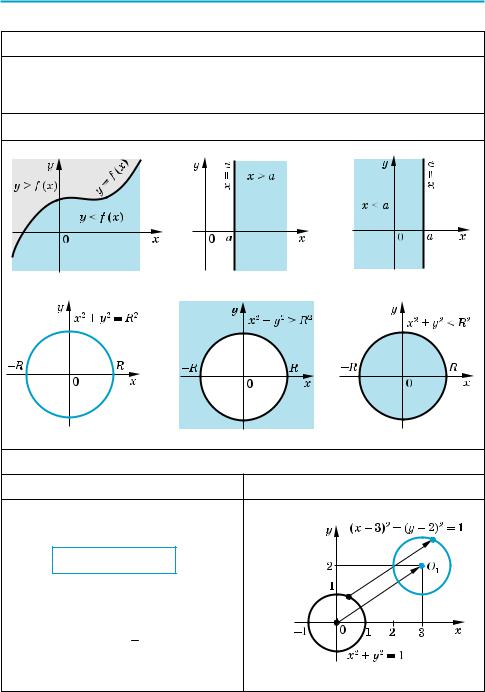
§8. Графіки рівнянь та нерівностей з двома змінними

Пр о д о в ж. т а б л. 21

2.Графіки рівнянь та нерівностей з двома змінними

Оз н а ч е н н я. Графіком рівняння (нерівності) з двома змінними х і у

називається множина всіх точок координатної площини з координатами (х; у), де пара чисел (х; у) є розв’язком відповідного рівняння (нерівності).

Графіки деяких рівнянь і нерівностей

3. Геометричні перетворення графіка рівняння F (x; y) = 0

F (x – a; y – b) = 0

Паралельне перенесення

графіка рівняння F (x; y) = 0

на вектор n(a; b).

101

РОЗДІЛ 1. Тригонометричні функції

П р о д о в ж. т а б л. 21

F (| x |; y) = 0

Частина графіка рівняння

F (х; у) = 0 праворуч від осі Оy (і на самій осі) залиша% ється без зміни, і ця сама частина відображується симетрично відносно осі Оy.

F (x; | y |) = 0

Частина графіка рівняння

F (х; у) = 0 вище від осі Ох

(і на самій осі) залишаєть% ся без зміни, і ця сама час% тина відображується си% метрично відносно осі Оx.

Пояснення й обґрунтування

1. Побудова графіків функцій виду y = f (x) + g (x). Якщо відомі графіки функцій y = f (x) та y = g (x), то можна побудувати орієнтовний вид графіка

функції y = f (x) + g (x), або y = f (x)æg (x), чи y = (1 ). Для цього досить зобра$

f x

зити в одній системі координат графіки функцій f (x) і g (x), а потім будувати шуканий графік за точками, виконуючи для кожного значення x (з області визначення заданої функції) необхідні операції над відрізками (або над дов$ жинами цих відрізків), які зображають відповідні ординати f (x) і g (x).

Приклад побудови графіка функції виду y = f (x) + g (x) наведено в таб$

зручно будувати графіки функцій y = f (x) і y = (1 ) не в одній системі коорди$

f x

нат, а в різних, розміщених так, щоб їхні осі ординат знаходилися на одній прямій).

Зауважимо, що такий спосіб побудови графіка функції не завжди дає мож$ ливість виявити всі характерні особливості поведінки графіка (часто це мож$ на зробити тільки в результаті спеціального дослідження функції, яке буде розглянуто в 11 класі), але в багатьох випадках наведений спосіб дозволяє отримати певне уявлення про вид графіка заданої функції.

102

§ 8. Графіки рівнянь та нерівностей з двома змінними

2. Графіки рівнянь та нерівностей з двома змінними. З поняттям графіка рівняння з двома змінними ви ознайомилися в курсі алгебри. Аналогічно вво$ диться і поняття графіка нерівності з двома змінними. Тому можна дати спільне означення цих графіків:

Графіком рівняння (нерівності) з двома змінними х і у називається мно жина всіх точок координатної площини з координатами (х; у), де пара чисел (х; у) є розв’язком відповідного рівняння (нерівності).

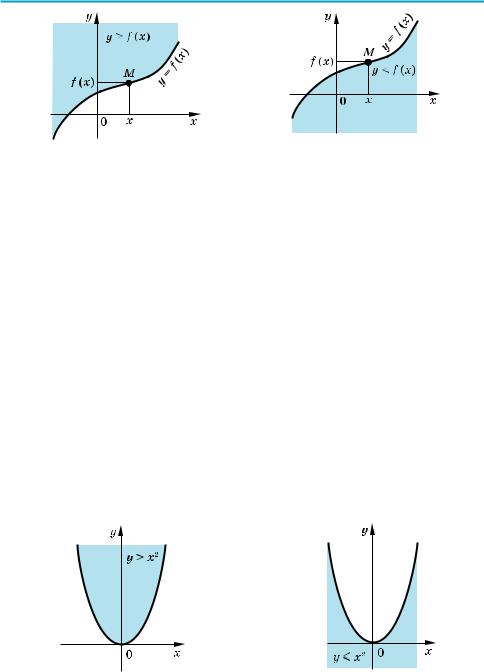
(Для побудови графіка нерівності y > f (x) (чи y < f (x)) досить мати графік функції y = f (x). Дійсно, за означенням графік функції y = f (x) складаєть$ ся з усіх точок M координатної площини з координатами (x; y) = (x; f (x)). Тоді для кожного значення x точки, координати яких задовольняють не$ рівності y > f (x), будуть знаходитися вище точки M (рис. 73, а), а точки, координати яких задовольняють нерівності y < f (x), будуть знаходитися нижче точки M (рис. 73, б). Таким чином,

графік нерівності y > f (x) складається з усіх точок координатної площи ни, які знаходяться вище від графіка функції y = f (x), а графік нерівності y < f (x) складається з усіх точок координатної площини, які знаходяться нижче від графіка функції y = f (x). )

Наприклад, на рисунку 74 зображено графік нерівності y > x2, а на рисун$ ку 75 графік нерівності y m x2. Оскільки точки графіка y = x2 не належать

103

РОЗДІЛ 1. Тригонометричні функції

графіку нерівності y > x2, то на першому графіку парабола y = x2 зображена штриховою лінією; але точки графіка y = x2 належать графіку нерівності y m x2, тому на другому графіку парабола y = x2 зображена суцільною лінією.

Аналогічно, якщо на координатній площині є пряма x = a, то

графіком нерівності x > a будуть усі точки координатної площини, які знаходяться праворуч від цієї прямої, а графіком нерівності x < a будуть усі точки координатної площини, які знаходяться ліворуч від цієї прямої.

Наприклад, на рисунку 76 зображено графік нерівності x > 2, а на рисун$ ку 77 — графік нерівності x m –1.

Зазначимо, що в тому випадку, коли на координатній площині є зобра$ ження кола x2 + y2 = R2, то

графіком нерівності x2 + y2 < R2 будуть усі точки координатної площини, які знаходяться всередині кола, а графіком нерівності x2 + y2 > R2 будуть всі точки координатної площини, які знаходяться поза колом.

(Дійсно, якщо на координатній площині розглянути точку M (x, y), то OM2 = x2 + y2 (O — початок координат). Якщо x2 + y2 = R2 (де R > 0), то OM2 = R2, отже, OM = R — точка M лежить на колі радіуса R з центром

у початку координат (рис. 78, а).

Якщо x2 + y2 < R2 , то OM2 < R2, отже, OM< R. Тобто нерівності x2 + y2 < R2 задовольняють координати всіх точок (і тільки цих точок), які знаходяться всередині круга, обмеженого колом радіуса R з центром у початку коорди$ нат (рис. 78, б).

Рис. 78

104

§ 8. Графіки рівнянь та нерівностей з двома змінними

(x – 1)2 + (y – 2)2 16

Якщо x2 + y2 > R2, то OM2 >R2, отже, OM > R . Тобто нерівності x2 + y2 > R2 задовольняють координати всіх точок (і тільки цих точок), які знаходяться поза кругом, обмеженим колом радіуса R з центром у початку координат (рис. 78, в).

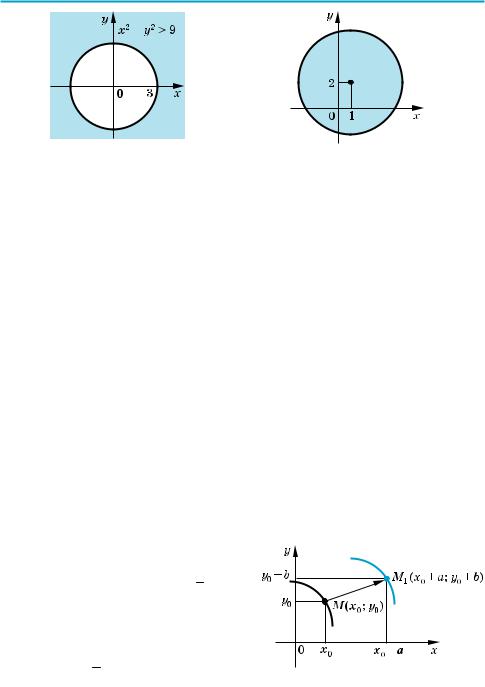
Аналогічно, якщо на площині є зображення кола (x – a)2 + (y – b)2 = R2, то графіком нерівності (x – a)2 + (y – b)2 < R2 будуть усі точки координатної площини, які знаходяться всередині кола, а графіком нерівності (x – a)2 + (y – b)2 > R2 будуть усі точки координатної площини, які знахо$ дяться поза колом. Наприклад, на рисунку 79 зображено графік нерівності x2 + y2 > 9, а на рисунку 80 — графік нерівності (x – 1)2 + (y – 2)2 16. )

3. Геометричні перетворення графіка рівняння F (x; y) = 0.

( За означенням графік рівняння

F (x; y) = 0 (1) складається з усіх точок M (x0; y0) координатної площини, координати (x0; y0) яких є розв’язками цього рівняння. Це означає, що при підста$ новці пари чисел (x0; y0) у задане рівняння воно перетворюється на пра$ вильну числову рівність, отже, F (x0; y0) = 0 — правильна рівність.

Розглянемо точку M1 (x0 + a; y0 + b). Якщо координати цієї точки підстави$ ти в рівняння

105

РОЗДІЛ 1. Тригонометричні функції

графік рівняння F (x – a; y – b) = 0 можна одержати з графіка рівнян ня F (x; y) = 0 паралельним перенесенням його на вектор n (a; b). )

(Для обґрунтування зв’язку між графіками F (х; у) = 0 і F (| x |; y) = 0 досить помітити, що при х l 0 рівняння F (| x |; y) = 0 збігається з рівнянням

F(х; у) = 0, отже, збігаються і їхні гра$ фіки праворуч від осі Оy і на самій осі.

Нехай точка M (x0; y0) (де х0 l 0 ) — одна

із спільних точок цих графіків. Тоді

F (x0; y0) = 0 — правильна рівність.

Розглянемо точку M1 (–x0 ; y0 ). Якщо ко$

ординати цієї точки підставити в рівнян$ ня F (| x |; y) = 0 і врахувати, що х0 l 0, то одержимо рівність F (x0; y0) = 0, яка є правильною. Тому координати точки M1

є розв’язками рівняння F (| x |; y) = 0, а значить, точка M1 належить гра$ фіку цього рівняння. Враховуючи, що точки M і M1 симетричні відносно осі Оy (рис. 82):

графік рівняння F (| x |; y) = 0 можна одержати з графіка рівняння F (х; у) = 0 так: частина графіка рівняння F (х; у) = 0 праворуч від осі Оy (і на самій осі) залишається без зміни, і ця ж сама частина відображується симетрично відносно осі Оy. )

Аналогічно обґрунтовується, що

для побудови графіка рівняння F (x; | y |) = 0: частина графіка рівнян ня F (х; у) = 0 вище від осі Ох (і на самій осі) залишається без зміни,

іця ж сама частина відображується симетрично відносно осі Оx.

Утаблиці 21 наведено найпростіші приклади використання геометричних перетворень графіків рівнянь. Указані співвідношення доводиться викорис$ товувати в завданнях типу: побудувати графік рівняння чи нерівності або зобразити на координатній площині множину точок, координати яких задо$ вольняють заданому рівнянню (нерівностi).

Приклади розв’язання завдань

106

§ 8. Графіки рівнянь та нерівностей з двома змінними

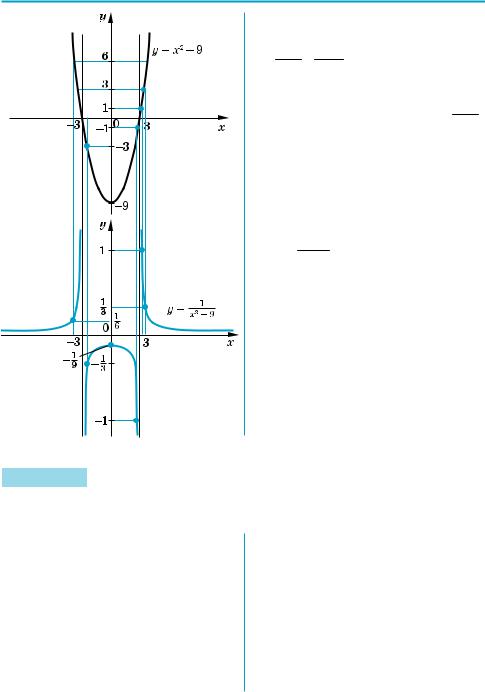
функція f (x) = x2 – 9 дорівнює нулю (x = ä 3), не існує графіка функції

y = (1 ) = 1 . Тому проведемо через

f x x2 − 9

ці точки вертикальні прямі, що не

перетинають графік функції y = (1 ).

f x

Потім для кожного значення x по$ ділимо 1 на відповідне значення ор$ динати f (x) (використовуючи те, що ординати f (x) відмічені на верхньому графіку). На рисунку синьою лінією зображено результат — графік функ$

штаб по осях Ох і Оу вибрано різний.)

Y

Приклад 2 Покажіть штриховкою на координатній площині множину то$

x2 + y m 0, чок, координати яких задовольняють системі x − y < 2.

107

РОЗДІЛ 1. Тригонометричні функції

Приклад 3 Побудуйте графік рівняння | х – у | + 2| х+у | = х +6.

О р і є н т и р

Для спрощення виразу з кількома модулями з двома змінними можна знайти нулі підмодульних виразів (тобто прирівняти їх до нуля) і роз% бити область визначення розглядуваного виразу на декілька частин, у кожній з яких знак кожного модуля розкривається однозначно.

Використовуючи цей орієнтир, одержуємо план розв’язання прикладу. Прирівняємо до нуля підмодульні вирази х – у = 0 (звідси у = х) і х + у = 0

(звідси у = – х ). Прямі у = х і у = –х розбивають координатну площину на чотири області. Укожній із цих областей знак кожного модуля розкриваєть$ ся однозначно і після перетворення одержаної рівності будується відповідна частина графіка заданого рівняння.

Р о з в ’ я з а н н я

X1. Область визначення: х R, у R.

2. х – у = 0 при у = х; х + у = 0 при у = –х.

108

§8. Графіки рівнянь та нерівностей з двома змінними

3.Прямі у = х і у = –х розбивають координатну площину на чотири частини,

укожній з яких позначено знаки першого і другого підмодульних виразів (рис. 83, а). (Будемо вважати, що кожна область береться разом з про$ менями, які її обмежують.) Дійсно, якщо точки знаходяться в області І або на її межі, то їхні координати задовольняють системі нерівностей

дульний вираз є від’ємним, а другий — додатним, і тому задане рівняння має вигляд: –(х – у) + 2(х + у) = х + 6. Звідси у = 2. Будуємо ту частину графіка цієї функції, що знаходиться в області І (рис. 83, б).

Отже, в області ІІ задане рівняння має вигляд: – (х – у) – 2(х + у) = х + 6. Звідси у = –4х – 6. Будуємо ту частину графіка цієї функції, що знаходить$ ся в області ІI.

ного рівняння маємо (х – у) + 2(х + у) = х + 6. Звідси у = –2x + 6. Остаточний вигляд графіка рівняння наведено на рисунку 83, б. Y

109

РОЗДІЛ 1. Тригонометричні функції

Запитання для контролю

1. Поясніть на прикладах, як можна, маючи графіки функцій y = f (x) та

y = g (x), побудувати ескіз графіка функції y = f (x) + g (x) та функції y = (1 ).

f x

2.Що називається графіком рівняння з двома змінними? Що називається графіком нерівності з двома змінними? Наведіть приклади.

3.Як, знаючи графік функції y = f (x), побудувати графік нерівності y > f (x) та нерівності y < f (x)? Наведіть приклади.

4.Як, знаючи графік рівняння F (x; y) = 0, можна побудувати графік рівнян$ ня F (x – a; y – b) = 0 та рівнянь F (|x|; y) = 0 і F (x; | y |) = 0? Наведіть приклади.

5*. Обґрунтуйте правила геометричних перетворень графіка рівняння

F(x; y) = 0 для одержання графіків рівнянь F (x – a; y – b) = 0, F (| x |; y) = 0,

F(x; | y |) = 0.

6.Поясніть на прикладі, як можна знайти на координатній площині множи$ ну точок, координати яких задовольняють системі нерівностей з двома змінними.

Вправи

4) (x – 2)2 + (y + 3 )2 > 4.

4.Покажіть штриховкою на координатній площині множину точок, коор$ динати яких задовольняють системі:

110