algebra10_нелін_дворівн

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Криворожский национальный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

x = (−1)n arcsin

+ πn, n Z.

.pdf

Скачиваний:

Добавлен:

22.03.2015

Размер:

5.24 Mб

Скачать

☆

<<< < Предыдущая 5 6 7 8 9 10 11 12 13 14 15 1617 / 4517 18 19 20 21 22 23 24 25 26 27 28 29 > Следующая >>>

§ 14. Розв’язування найпростіших тригонометричних рівнянь
2x − π = ± π + 2πn,			дження значення виразу 2x − π, який
	3	4			3
x = π ± π + πn, n Z.			стоїть під знаком косинуса. Після
x = π ± π + πn, n Z.			цього з одержаного лінійного рівян$
6	8		цього з одержаного лінійного рівян$
6	8		ння знaходимо х.
Відповідь: π ± π + πn, n Z. Y			ння знaходимо х.
Відповідь: π ± π + πn, n Z. Y
	6	8
14.2. РІВНЯННЯ sin x = a
				Т а б л и ц я 31
	1. Графічна ілюстрація і розв’язки рівняння sin x = a
		Графічна ілюстрація
	Розв’язки			Приклади
	sin x = a		1. X sinx = 1 ,
			2
\| a \| > 1		\| a \| m 1	x = (−1)n arcsin 1 + πn, n Z.
				2
Коренів немає				n π
Коренів немає			x = (−1) 6 + πn, n Z. Y
			x = (−1) 6 + πn, n Z. Y
x = (–1)n arcsin a + πn, n Z			2. X sinx =	3.	3 > 1. Y
			Коренів немає, оскільки		3 > 1. Y
	2. Окремі випадки розв’язування рівняння sin x = a
			sin x = 0 x = πk, k Z
			sin x = 1	x = π + 2πk, k Z
				2
			sin x = –1	x = − π + 2πk,	k Z
				2
			161

РОЗДІЛ 2. Тригонометричні рівняння і нерівності

Пояснення й обґрунтування

1. Розв’язки рівняння sin x = a. При | a | > 1 рівняння не має коренів, оскільки | sin x | m1 для будь$якого x (пряма y = a на рисунку 94 при a > 1 або при a < –1 не перетинає графік функції y = sin x).

Нехай | a | m 1. Тоді пряма у = а перетинає графік функції y = sin x. На проміжку −2π; 2π функція y = sin x зростає від –1 до 1, тому рівняння

sin x = a має тільки один корінь x 1 = arcsin a на цьому проміжку (рис. 94) (і для цього кореня sin x = a).

На проміжку 2π; 32π функція y = sin x спадає від 1 до –1, тому рівняння

sin x = a має на цьому проміжку теж тільки один корінь x2 = π – arcsin a (рис. 94). Для перевірки правильності запису значення другого кореня x2 заз$

начимо, що x2 = π – x1, тоді sin x2 = sin (π – x1) = sin x1 = a. Тобто х2 — корінь рівняння sin x = a.

Отже, на проміжку −2π; 32π (довжиною 2π) рівняння sin x = a при | a | m 1

має тільки корені x1 = arcsin a, x2 = π – arcsin a.

Враховуючи, що функція y = sin x періодична з періодом 2π, усі інші корені відрізняються від знайдених на 2πk (k Z), тобто одержуємо такі формули

коренів рівняння sin x = a при \| a \| m 1:
x = arcsin a + 2πk;	(1)
x = π – arcsin a + 2πk, k Z.	(2)

Усі значення коренів рівняння sin x = a при | a | m 1, які дають формули (1) і (2), можна записати за допомогою однієї формули

x = (–1)n arcsin a + πn, n Z

(3)

Дійсно, з формули (3) при парному n = 2k одержуємо: x = arcsin a + 2πk — формулу (1), а при непарному n = 2k + 1 — формулу: x = –arcsin a + π(2k + 1) = = π – arcsin a + 2πk, тобто формулу (2).

Рис. 94

162

§ 14. Розв’язування найпростіших тригонометричних рівнянь

	2. Окремі випадки розв’язування рів
	няння sin x = a.
	( Корисно пам’ятати спеціальні запи$
	си розв’язків при a = 0, a = –1, a = 1,
	які можна легко одержати, викорис$
	товуючи як орієнтир одиничне коло
	(рис. 95).
	Враховуючи, що синус дорівнює ор$
	динаті відповідної точки одиничного	Рис. 95
	кола, одержуємо, що sin x = 0, якщо	Рис. 95
	кола, одержуємо, що sin x = 0, якщо
	відповідною точкою одиничного кола є точка C або точка D. Тоді
	x = πk, k Z.

Аналогічно sin x = 1 тоді і тільки тоді, коли відповідною точкою одинично$

го кола є точка А, отже, x = π + 2πk, k Z.

Також sin x = –1 тоді і тільки тоді, коли відповідною точкою одиничного

кола є точка В, отже, x = − π + 2πk, k Z. )

Приклади розв’язання завдань

Приклад 1 Розв’яжіть рівняння sinx = − 3 .

Р о з в ’ я з а н н я

x = (−1)n (− π3 )+ πn, n Z.

Відповідь:

(− 1 )n (− 3π )+ π n, n Z.Y

К о м е н т а р

Оскільки − 3 < 1, то задане рів$

няння виду sin x = a має корені, які можна знайти за формулою (3).

		3
Для обчислення arcsin	−
		2

можна скористатися формулою:

arcsin (–a) = –arcsіn a.

Тоді

		3		3		π
arcsin	−		= −arcsin		= −		.
		2		2		3

З а у в а ж е н н я. Відповідь до прикладу 1 часто записують у вигляді

x = (−1)n+1 π + πn, n Z, але такий запис не є обов’язковим.

163

	РОЗДІЛ 2. Тригонометричні рівняння і нерівності
Приклад 2	Розв’яжіть рівняння sinx = π .
						2
Р о з в ’ я з а н н я						К о м е н т а р
X Оскільки 2π						π
X Оскільки 2π	>1, то коренів немає.					Оскільки 2 >1, то задане рівнян$
Відповідь: коренів немає. Y						ня не має коренів (тобто формулою (3)
Відповідь: коренів немає. Y						не можна скористатися).
						не можна скористатися).
Приклад 3	Розв’яжіть рівняння sin(2x + 4π )= 12.
Р о з в ’ я з а н н я						К о м е н т а р
X 2x + π = (−1)n arcsin 1 + πn, n Z,						Оскільки 1 <1, то можна скориста$
4				2		2
2x + π =		(−1)n π + πn,				тися формулою (3) для знаходжен$
4					6	ня значення виразу 2x + π , а потім з
n π			π		πn	ня значення виразу 2x + π , а потім з
n π			π		πn	4
x = (−1)		−		+	2 , n Z.	4
x = (−1)	12	−	8	+	2 , n Z.	одержаного лінійного рівняння зна$
n π			π	+	πn	йти змінну х.
Відповідь: (−1)	12 −		8	+	2 , n Z. Y
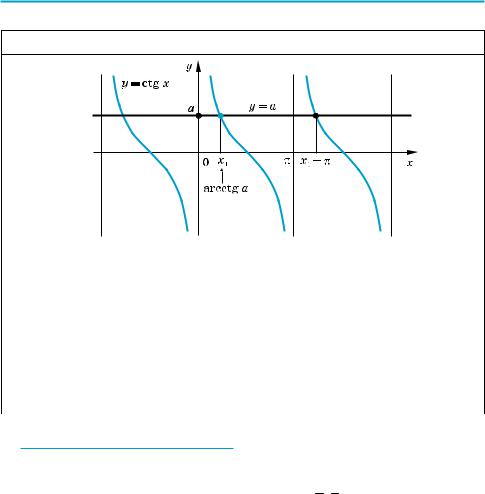
14.3. РІВНЯННЯ tg x = a і ctg x = a
						Т а б л и ц я 32
1. Графічна ілюстрація і розв’язки рівняння tg x = a
Формула						Приклад
tg x = a						tg x = 1.
x = arctg a + πn, n Z						tg x = 1.
x = arctg a + πn, n Z						X x = arctg 1 + πn, n Z.
Окремий випадок						X x = arctg 1 + πn, n Z.
Окремий випадок						x = π + πn, n Z. Y
tg x = 0						x = π + πn, n Z. Y
tg x = 0						4
х = πn, n Z
					164

§14. Розв’язування найпростіших тригонометричних рівнянь

Пр о д о в ж. т а б л. 32

2.Графічна ілюстрація і розв’язки рівняння сtg x = a

	Формула			Приклад


	сtg x = a
x = arсctg a + πn, n Z
				сtg x = 7.
	Окремий випадок			сtg x = 7.
	Окремий випадок			X x = arcctg 7 + πn, n Z. Y

	сtg x = 0
	сtg x = 0
	x =	π	+ πn, n Z
	x =		+ πn, n Z
	2

Пояснення й обґрунтування

1. Розв’язки рівнянь tg x = a і ctg x = a.

( Розглянемо рівняння tg x = a. На проміжку (− 2π; 2π )функція y = tg x зрос$

тає (від –× до +×), тому рівняння tg x = a при будь$якому значенні a має тільки один корінь х1 = arctg a на цьому проміжку (рис. з пункту 1 табл. 32). Враховуючи, що функція y = tg x періодична з періодом π, усі інші корені відрізняються від знайденого на πn (n Z), тобто одержуємо таку формулу коренів рівняння tg x = a:

x = arctg a + πn, n Z

(1)

При a = 0 arctg 0 = 0, отже, рівняння tg x = 0 має корені x = πn, n Z. )

(Розглянемо рівняння ctg x = a. На проміжку (0; π) функція y = ctg x спадає (від +× до –×), тому рівняння ctg x = a при будь$якому значенні a має тільки один корінь x1 = arcctg a на цьому проміжку (рис. з пункту 2 табл. 32).

165

РОЗДІЛ 2. Тригонометричні рівняння і нерівності

Враховуючи, що функція y = ctg x періодична з періодом π, усі інші корені відрізняються від знайденого на πn (n Z), тобто одержуємо таку формулу коренів рівняння ctg x = a:

x = arcctg a + πn, n Z

(2)

При a = 0 arcctg 0 = π , отже, рівняння ctg x = 0 має корені x =

+ πn, n Z.

Приклади розв’язання завдань

Розв’яжіть рівняння tg x = − 3.

Приклад 1

Р о з в ’ я з а н н я

К о м е н т а р

X x = arctg(− 3 )+ πn, n Z.

Рівняння tg x = амає розв’язки при

будь$якому значенні а, отже, завжди

x = −

+ πn, n Z.

можна скористатися формулою (1):

x = arctg a + πn, n Z.

Відповідь: −

+ πn, n Z. Y

Для знаходження arctg (− 3 )

можна використати формулу

arctg (–a) = –arctg a. Тоді

arctg (− 3 )= −arctg 3 = −

Розв’яжіть рівняння tg (

−

)= 1.

Приклад 2

Р о з в ’ я з а н н я

X	x	−	π	= arctg1+ πn, n Z,
X		−		= arctg1+ πn, n Z,
2		4
					x	−	π	=	π	+ πn,
		2				−		=		+ πn,
		2				4		4

x = π + 2πn, n Z.

Відповідь: π + 2πn, n Z. Y

К о м е н т а р

Спочатку за формулою (1) знайде$

мо значення виразу x2 − π4 , а потім з

одержаного лінійного рівняння знай$ демо значення змінної х.

Приклад 3 Розв’яжіть рівняння ctg x = 5.

Р о з в ’ я з а н н я

X x = arcctg 5 + πn, n Z.

Відповідь: arcctg 5 + πn, n Z. Y

К о м е н т а р

Рівняння ctg x = a має розв’язки при будь$якому значенні а, отже, зав$ жди можна скористатися форму$ лою (2):

x = arcctg a + πn, n Z.

166

§ 14. Розв’язування найпростіших тригонометричних рівнянь

Враховуючи, що arcctg 5 не є таб$ личним значенням (див. табл. 8, на$ ведену на с. 47), одержана формула дає кінцеву відповідь.

Приклад 4 Розв’яжіть рівняння ctg (3x + 6π)= −1.

Р о з в ’ я з а н н я

X 3x + π = arcctg(−1)+ πn, n Z,

3x + π = 3π + πn,

6 4

x = 7π + πn , n Z.

36 3

Відповідь: 7π + πn , n Z. Y

36 3

Запитання для контролю

К о м е н т а р

Спочатку за формулою (2) знайде$

мо значення виразу 3x + π , а потім з

одержаного лінійного рівняння знай$ демо значення змінної х.

Для знаходження arcctg (–1) можна скористатися формулою arcctg (–a) = π – arcctg a. Тоді

arcctg(−1)= π − arcctg1 = π − π = 3π .

4 4

1.Які рівняння називають найпростішими тригонометричними?

2.Назвіть формули розв’язування найпростіших тригонометричних рівнянь. У яких випадках не можна знайти корені найпростішого тригонометрич$ ного рівняння за цими формулами?

3*. Виведіть формули розв’язування найпростіших тригонометричних рівнянь.

4*. Обґрунтуйте формули розв’язування найпростіших тригонометричних рівнянь для окремих випадків (для sin x = a i cos x = a випадки a = 0; 1; –1, для tg x = a i ctg x = a випадок a = 0).

Вправи

Розв’яжіть рівняння (1–11).

1°. 1)	cosx =		2	;	2)	cosx =	3;			3)	cosx = −		1		;	4)	cosx = −	2		.
			2								2							2
2°. 1)	sinx =	1	;		2)	sinx =	3		;	3)	sinx = −	1		;		4)	sinx = −	5	.
																		5

	2						2				2							2
3°. 1) tg x = 1;					2)	tgx =	1	;		3) tg x = –1;						4)	tg x = −	3.
3°. 1) tg x = 1;					2)	tgx =	3	;		3) tg x = –1;						4)	tg x = −	3.
							3

167

РОЗДІЛ 2. Тригонометричні рівняння і нерівності

4°. 1) ctg x = 1;	2) ctgx =	1	;

	3

3) ctg x = –1;

4) ctg x = − 3.

5.	1) sin x = –0,6;																										2) cos x = 0,3;							3) tg x = –3,5;																					4) ctg x = 2,5.
6.	1)	cos 2x =											1				;										2) sin 4x = 0;							3) tg 3x = 1;																					4) tg 4x = 3.
6.	1)	cos 2x =															;										2) sin 4x = 0;							3) tg 3x = 1;																					4) tg 4x = 3.
												2
7.	1)	sin(−				t		)				= −												2			; 2) cos	t	= −	2			;	3)	tg(−					x		)=							1			;			4) ctg	x	= 1.
7.	1)	sin(−			4			)				= −												2			; 2) cos	t	= −	2			;	3)	tg(−					x		)=							1			;			4) ctg	x	= 1.
					4																			2			5			2					3														3						7
																																																	3
8°.	1)	sin 2x =										2										;					2) cos	x	= −		1	;		3)	sin	x			=						1			;							4) cos 4x = 0.
												2															3			2					4							2
9.	1)	sin(−				x			)=															2		; 2) cos(−2x) = −							3	; 3)	tg(−4x) =															1				;	4) ctg(−			x	)= 1.
9.	1)	sin(−							)=																	; 2) cos(−2x) = −								; 3)	tg(−4x) =																			;	4) ctg(−			x	)= 1.
					3							2																		2																			3						2
																																																	3
10.	1)	2 cos(					x				−					π				)=							3;							2)	3tg(								x				+ π )= 3;
10.	1)	2 cos(									−					π				)=							3;							2)	3tg(												+ π )= 3;
					2							6																														3							6
	3)	2 sin(3x −																	π						)= − 2;									4)	sin(		x				− π )+ 1 = 0.
	3)	2 sin(3x −																							)= − 2;									4)	sin(						− π )+ 1 = 0.
												4																							2							6
11.	1)	cos(π − 2x)= −1;																																2)	tg(	π		−						x				)= −1;
11.	1)	cos(π − 2x)= −1;																																2)	tg(			−										)= −1;
		6																																	4							2
	3)	2 sin(				π				−					x				)=								3;							4)	2 cos(							π				− 3x)=									2.
	3)	2 sin(								−									)=								3;							4)	2 cos(							4				− 3x)=									2.
					3							4																														4
Знайдіть корені рівняння на заданому проміжку (12–13).
12*. 1)		sin 3x =										2											,				[0, 2π];							2)	cos 3x =														3		, [–π, π];
12*. 1)		sin 3x =																					,				[0, 2π];							2)	cos 3x =																, [–π, π];
												2																														2
	3)	tg	x	=			3							,											[–3π, 3π];									4) ctg 4x = –1,																					[0, π].
	3)	tg		=										,											[–3π, 3π];									4) ctg 4x = –1,																					[0, π].
		2			3
13*. 1)		sin 3x = −																1			,						[–4, 4];							2)	sin	x			= 0,												[–12, 18];
13*. 1)		sin 3x = −																			,						[–4, 4];							2)	sin				= 0,												[–12, 18];
												2																							2
	3) cos x = 1,																								[–6, 16];									4)	cos3x = −														2				,		[1, 7].
	3) cos x = 1,																								[–6, 16];									4)	cos3x = −																		,		[1, 7].
																																																	2

168

§15	РОЗВ’ЯЗУВАННЯ ТРИГОНОМЕТРИЧНИХ РІВНЯНЬ,
	ЯКІ ВІДРІЗНЯЮТЬСЯ ВІД НАЙПРОСТІШИХ

Як правило, розв’язування тригонометричних рівнянь зводиться до роз$ в’язування найпростіших рівнянь за допомогою перетворень тригонометрич$ них виразів, розкладання на множники та заміни змінних.

15.1.ЗАМІНА ЗМІННИХ ПРИ РОЗВ’ЯЗУВАННІ ТРИГОНОМЕТРИЧНИХ РІВНЯНЬ

Слід пам’ятати загальний орієнтир, коли заміна змінних може виконува$ тися без перетворення заданих тригонометричних виразів.

Якщо до рівняння, нерівності або тотожності змінна входить в одному і тому самому вигляді, то зручно відповідний вираз із змін ною позначити однією буквою (новою змінною).

Приклад 1 Розв’яжіть рівняння 2 sin2 x – 7 sin x + 3 = 0.

Р о з в ’ я з а н н я

X Нехай sin x = t, тоді одержуємо:
2t2 – 7t + 3 = 0.
Звідси t		= 3; t =	1	.
	1
		2	2

1. При t = 3 маємо sin x = 3 — рівнян$ ня не має коренів, оскільки | 3 | > 1.

2. При t =	1	маємо sinx =	1	,
2		2

тоді x = (−1)n arcsin 1 + πn,

x = (−1)n 6π + πn, n Z.

Відповідь: (−1)n 6π + πn, n Z. Y

К о м е н т а р

Аналізуючи вигляд цього рівнян$ ня, помічаємо, що до нього входить тільки одна тригонометрична функ$ ція sin x. Отже, зручно ввести нову змінну sin x = t.

Після розв’язування квадратного рівняння необхідно виконати оберне$ ну заміну і розв’язати одержані най$ простіші тригонометричні рівняння.

обернену заміну виконувати тільки для t = 1 .

169

РОЗДІЛ 2. Тригонометричні рівняння і нерівності

Приклад 2 Розв’яжіть рівняння tg3 2x – tg 2x = 0.

К о м е н т а р

До заданого рівняння змінна входить тільки у вигляді tg 2x. Отже, зручно ввести нову змінну tg 2x = t. Після виконання оберненої заміни і розв’язуван$ ня одержаних найпростіших тригонометричних рівнянь слід до відповіді за$ писати всі одержані корені.

Р о з в ’ я з а н н я

X Нехай tg 2x = t. Тоді одержуємо t3 – t = 0. Звідси t (t2 – 1) = 0, тобто t = 0 або

t2 – 1 = 0. З останнього рівняння маємо t2 = 1, тоді t = 1 або t = –1.

Виконуємо обернену заміну:

При t = 0 маємо tg 2x = 0, тоді 2x = πn, n Z. Отже, x =

πn

, n Z.

При t = 1 маємо tg 2x = 1, тоді 2x = arctg 1 + πm, 2x =

+ πm. Отже,

πm

x =

, т Z.

При t = –1 маємо tg 2x = –1, тоді 2x = arctg (–1) + πk, 2x = −

+ πk. Отже,

πk

x = −

, k Z.

Відповідь:

πn

, n Z;

πm

, т Z; − π +

πk

, k Z. Y

При пошуку плану розв’язування більш складних тригонометричних рівнянь можна скористатися таким о р і є н т и р о м.

1.Пробуємо звести всі тригонометричні функції до одного аргументу.

2.Якщо вдалося звести до одного аргументу, то пробуємо всі тригоно% метричні вирази звести до однієї функції.

3.Якщо до одного аргументу вдалося звести, а до однієї функції — ні, то пробуємо звести рівняння до однорідного.

4.В інших випадках переносимо всі члени в один бік і пробуємо одержа ти добуток або використовуємо спеціальні прийоми розв’язування.

15.2.РОЗВ’ЯЗУВАННЯ ТРИГОНОМЕТРИЧНИХ РІВНЯНЬ ЗВЕДЕННЯМ ДО ОДНІЄЇ ФУНКЦІЇ (З ОДНАКОВИМ АРГУМЕНТОМ)

Приклад 1 Розв’яжіть рівняння соs 2x – 5 sin x – 3 = 0.

Р о з в ’ я з а н н я

XВикористовуючи формулу косину$ са подвійного аргументу та основ$ ну тригонометричну тотожність, одержуємо:

К о м е н т а р

Усі тригонометричні функції зво$ димо до одного аргументу х, викори$ стовуючи формулу

соs2 2x = cos2 x – sin2 x.

170

<<< < Предыдущая 5 6 7 8 9 10 11 12 13 14 15 1617 / 4517 18 19 20 21 22 23 24 25 26 27 28 29 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.03.20158.49 Mб8978-966-00-1063-5.pdf
#
07.03.2016315.39 Кб16ADMINISTRATIVNO_PRAVOVIJ_STATUS_MON-2.doc
#
07.03.2016359.42 Кб11AGRARNA_POLITIKA_UTsR_DIPLOMNA_ROBOTA.doc
#
21.11.2019178.18 Кб5Alekhina_glava4-97.doc
#
09.11.20194.5 Mб21Alesinskaya_Reshenie_zadach_Ekonom_metody_model...doc
#
22.03.20155.24 Mб59algebra10_нелін_дворівн.pdf
#
07.03.20161.34 Mб214AMMA.doc
#
12.11.20181.63 Mб22Angl.doc
#
30.04.201517.56 Кб45angl.docx
#
22.03.201533.28 Кб278Annotatsia_proizvedenia_Groza.doc
#
22.03.201545.11 Mб46Antichnaya_mifologia_Entsiklopedia.rtf