Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Криворожский национальный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

algebra10_нелін_дворівн

.pdf

Скачиваний:

Добавлен:

22.03.2015

Размер:

5.24 Mб

Скачать

☆

<<< < Предыдущая 11 12 13 14 15 16 17 18 19 20 21 2223 / 4523 24 25 26 27 28 29 30 31 32 33 34 35 > Следующая >>>

§ 20. Тригонометричні рівняння з параметрами

І.

x =

2 + πk,

(

)

При

, з рівняння (1) одержуємо tg

π +

2πk

= actg

+ πk ,

тобто 0 = aæ0 — рівність, правильну при будь яких значеннях a. Отже,

при всіх значеннях параметра a задане рівняння має корені

x =

+ πk, k Z

2tg x =

a ,

II. При x ≠

+ πk

одержуємо рівняння (2) :

1 − tg2 x

tgx

яке на ОДЗ рівносильне рівнянню 2 tg2 x = a – a tg2 x. Звідси

(2+ a) tg2 x = a.

(3)

1)Якщо a = –2, то коренів немає.

2)Якщо a ≠ –2, то рівняння (3) рівносильне рівнянню

tg2 x =

(4)

a + 2

а) Якщо

< 0, то коренів немає.

a +

Розв’язавши нерівність

< 0 методом інтервалів

a + 2

(див. рисунок), одержуємо –2 < а < 0.

Отже, при –2 < а < 0

коренів немає

б) Якщо

= 0 (тобто а = 0), одержуємо рівняння tg x = 0, яке має корені

a +

х = πk, k Z. Але ці корені не входять до ОДЗ заданого рівняння. Отже, і при а = 0 коренів немає .

в) Якщо

> 0

(тобто а < –2 або а > 0), то з рівняння (4) одержуємо

a +

+ πl, l Z.

tgx = ±

Звідси x = arctg

a +

a + 2

З’ясуємо, при яких значеннях а одержані корені рівняння (4) не входять до ОДЗ. Для цього досить у рівняння (4) замість аргументу х підставити «за боронені» значення. Враховуючи, що функції, які входять до запису задано

го рівняння (1), мають спільний період Т = π (tg 2x має період T = π, а ctg x

1 2

має період Т2 = π), досить підставити ці значення тільки на одному періоді, наприклад, на проміжку [0; π]. У цьому проміжку до ОДЗ не входять такі

значення: 0; π; 3π; π. При х = 0 або х = π з рівняння (4) одержуємо рівність

a			= 0, тобто а = 0. Випадок а = 0 ми вже дослідили (коренів немає). При
a +	2

x =		π		або x =	3π	з рівняння (4) одержуємо	a		= 1. Але при жодному значен

	4			4			a +	2

221

РОЗДІЛ 2. Тригонометричні рівняння і нерівності

ні а ця рівність не може виконуватися. Отже, при всіх значеннях а < –2 або

а > 0 одержані розв’язки

x =arctg

+πl,

входять до ОДЗ

a +2

початкового рівняння.

Зобразимо одержані відповіді:

1) x =

+ πk, k Z

2) x =arctg

+πl, l Z

a +2

Відповідь: 1) якщо –2 m a m 0, то x =

+ πk, k Z;

+ πk, k Z, x

+πl, l Z. Y

2) якщо a < –2 або а > 0, то x =

=arctg

a +2

20.2. ДОСЛІДНИЦЬКІ ЗАДАЧІ З ПАРАМЕТРАМИ

Крім завдань з параметрами, у яких вимагається «розв’язати рівняння або нерівність», часто пропонуються дослідницькі завдання з параметрами. Такі завдання іноді вдається розв’язати за допомогою безпосередніх обчис лень: розв’язати задане рівняння або нерівність і після цього дати відповідь на запитання задачі. Проте досить часто дослідницькі завдання не вдається розв’язати безпосередніми обчисленнями (або такі обчислення є дуже гро міздкими), і тому доводиться спочатку обґрунтувати якусь властивість зада ного рівняння або нерівності, а потім, користуючись цією властивістю, вже давати відповідь на запитання задачі.

Розглянемо деякі з таких властивостей. Наприклад, беручи до уваги парність функцій, що входять до запису заданого рівняння, використовуєть ся такий о р і є н т и р.

Якщо в рівнянні f (х) = 0 функція f (х) є парною або непарною, то разом з будь яким коренем α ми можемо вказати ще один корінь цього рівняння (–α).

Приклад 1 Знайдіть усі значення параметра а, при яких рівняння

a2 cos2 x – x2 – a = 0 (1) має єдиний корінь.

Р о з в ’ я з а н н я

X Функція f (x) = a2 cos2 x – x2 – a є парною (D(f) = R, f (–x) = f (x)). Якщо x = α — корінь рівняння (1), то x = –α теж є коренем цього рівняння. Тому

К о м е н т а р

Помічаємо, що в лівій частині за даного рівняння стоїть парна функ ція, і використовуємо орієнтир, наве дений вище. Дійсно, якщо x = α —

222

§ 20. Тригонометричні рівняння з параметрами

єдиний корінь у заданого рівняння може бути тільки тоді, коли α = –α, тобто α = 0. Отже, єдиним коренем заданого рівняння може бути тільки х = 0.

Якщо х = 0, то з рівняння (1) одер жуємо а2 – а = 0, тобто а(а – 1) = 0. Звідси а = 0 або а = 1.

При а = 0 рівняння (1) перетво рюється на рівняння х2 = 0, яке має єдиний корінь х = 0. Отже, а = 0 задо вольняє умові задачі.

При а = 1 маємо рівняння cos2 x – x2 – 1 = 0, тобто

cos2 x = 1 + х2.

(2)

Оскільки cos2 x m 1, а 1 + х2 l 1, то рівняння (2) рівносильне системі

cos x2 = 1,

+ =

1 x2 1.

З другого рівняння системи одер жуємо х = 0, що задовольняє і першо му рівнянню. Отже, ця система, а зна чить, і рівняння (2) має єдиний роз в’язок х = 0. Отже, а = 1 також задо вольняє умові задачі.

Відповідь: а = 0, а = 1. Y

корінь рівняння f (x) = 0, то f (α) = 0 — правильна числова рівність. Врахову

ючи парність функції f (x), маємо f (−α) = f (α) = 0. Отже, x = −α теж

корінь рівняння f (x) = 0. Єдиний ко рінь у цього рівняння може бути тіль ки тоді, коли корені α і − α співпада ють. Тоді x = α = −α = 0.

З’ясуємо, чи існують такі значен ня параметра а, при яких х = 0 є ко ренем рівняння (1). (Це а = 0 і а = 1.)

Оскільки значення а = 0 і а = 1 ми одержали з умови, що х = 0 — корінь рівняння (1), то необхідно перевіри ти, чи дійсно при цих значеннях а за дане рівняння матиме єдиний корінь.

Для розв’язування рівняння (2) оцінимо його ліву і праву частини:

f (x) = cos2 x, g (x) = 1 + x2.

cos2 x =	1 + x2
0 m f (x) m 1	g (x) l 1
		cosx2	= 1,
			= 1.
		1+ x2	= 1.

При розв’язуванні деяких дослідницьких задач з параметрами допомагає використання такого о р і є н т и р у.

Якщо в умові задачі з параметрами говориться про те, що задане рівнян ня чи нерівність мають розв’язками всі значення змінної з деякої множини, то іноді корисно підставити конкретні значення змінної із заданої множи ни і одержати деякі обмеження на параметр.

Приклад 2 Знайдіть усі пари чисел (a, b), для яких коренями рівняння a (cos x – 1) + b2 = cos (ax + b2) – 1 (1)

будуть всі дійсні числа.

Р о з в ’ я з а н н я

X Якщо коренями заданого рівнян ня є всі дійсні числа, то коренем буде і число нуль.

К о м е н т а р

Ми не в змозі розв’язати задане рівняння (але його і не вимагають роз в’язати), тому скористаємося тим, що

223

РОЗДІЛ 2. Тригонометричні рівняння і нерівності

При х = 0 одержуємо b2 = cos b2 – 1, тоді

1 + b2 = cos b2.

(2)

Враховуючи, що 1 + b2 l 1, а cos b2 m1, одержуємо, що рівняння (2)

1 + b2 = 1, рівносильне системі cos b2 = 1.

З першого рівняння системи одер жуємо b = 0, що задовольняє і друго му рівнянню. Отже, ця система, а зна чить, і рівняння (2) мають єдиний розв’язок b = 0.

Таким чином, умова задачі може виконуватися тільки при b = 0.

При b = 0 рівняння (1) перетво рюється на рівняння

а (cos x – 1) = cos (ax) – 1. (3) Але за умовою коренями рівняння (1), а значить, і рівняння (3) повинні бути всі дійсні числа, отже, коренем буде і число 2π. При х = 2π одержуємо 0 = cos (2πa) – 1, тоді cos (2πa) = 1, тобто 2πa = 2πk, k Z. Отже, a = k, k Z (таким чином, а — ціле число). Якщо коренями рівняння (3) є всі

дійсні числа, то коренем будеі число			π	.
дійсні числа, то коренем будеі число			2	.
			2
При x =	π	одержуємо −a = cos (π a)− 1.
При x =		одержуємо −a = cos (π a)− 1.
2		2

Оскільки cos (2π a) при цілих зна

ченнях а набуває тільки значень 1; 0; –1, то а може набувати тільки зна чень 0; 1; 2.

Якщо а = 0 (і b = 0), то рівняння

(1) має вигляд 0 (cos x – 1) = cos 0 – 1, тобто 0(cos x – 1) = 0, і його коренями є всі дійсні числа. Отже, пара чисел (a, b) = (0; 0) задовольняє умові за дачі.

Якщо а = 1 (і b = 0), то рівняння

(1) має вигляд cos x – 1 = cos x – 1,

за умовою його коренями будуть усі дійсні числа, і підставимо замість змінної х якісь конкретні значення.

Для підстановки найчастіше виби рають такі з них, які дозволяють пе ретворити якийсь вираз на нуль. Так, при х = 0 вираз у перших дужках до рівнює нулю. Розв’язуючи одержане рівняння (2) відносно b, отримуємо єдиний розв’язок b = 0.

Якщо b ≠ 0, то рівність (1) не може бути правильною при х = 0, тобто х = 0 не буде коренем заданого рівнян ня, а значить, при цих значеннях b рівняння (1) не може мати коренями всі дійсні числа.

Спробуємо ще раз перетворити ви раз у перших дужках на нуль, вико ристовуючи те, що число 2π є періо дом функції cos x, отже, через 2π зна чення в перших дужках буде повто рюватися (підставляємо х = 2π).

Потім спробуємо перетворити на нуль cos x (підставляємо x = 2π ).

При цілому а значення 2π a на оди

ничному колі зображуються на кінцях горизонтального та верти кального діаметрів, отже, значення

cos (2π a) можуть бути тільки: 1, –1

і 0.

Оскільки значення a і b ми отри мали при підстановці в задане рівнян ня тільки трьох значень х, то необхі дно перевірити, чи будуть усі дійсні числа при цих значення a і b кореня ми заданого рівняння, тобто пере вірити, чи буде рівняння (1) перетво рюватися на правильну рівність при всіх дійсних значеннях х.

224

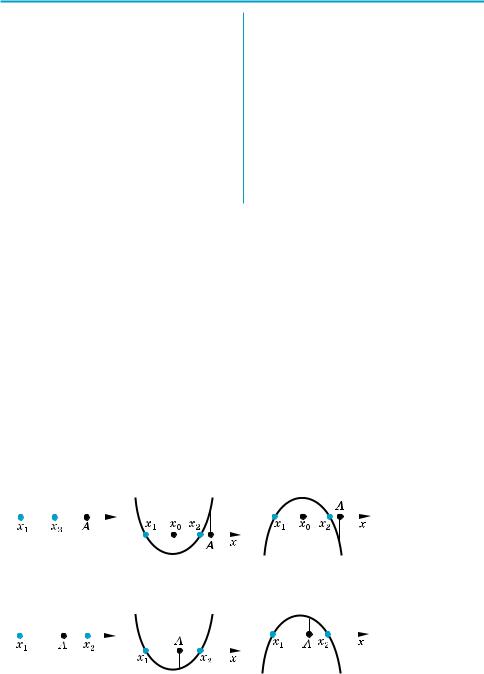
§ 20. Тригонометричні рівняння з параметрами

і його коренями є всі дійсні числа.	У випадку, коли а = 2 і b = 0, одер
Отже, пара чисел (a, b) = (1; 0) задо	жуємо, що cos 2x = 2 cos x – 1. Якби
вольняє умові задачі.	ця рівність була правильною при всіх
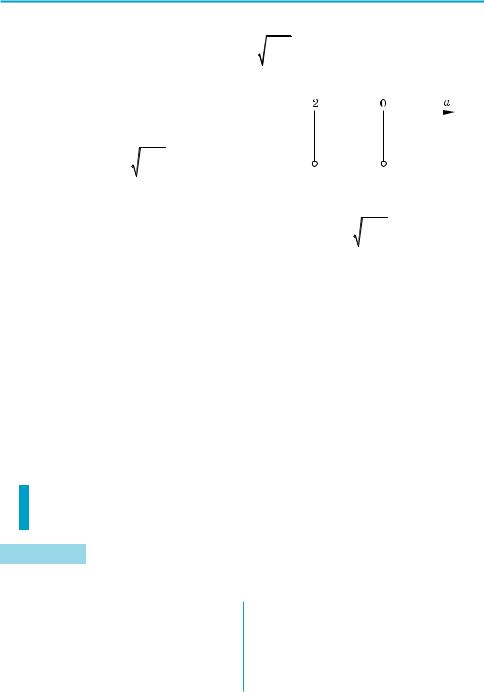
Якщо а = 2 (і b = 0), то рівняння (1)	значеннях х, то це була б ще одна фор
має вигляд 2(cos x – 1) = cos 2х – 1.	мула косинуса подвійного аргументу.
Коренями цього рівняння не можуть	Але такої формули немає, отже, мож
бути всі дійсні числа, оскільки коре	на вказати якесь значення х, при яко
нем не є x = π (при підстановці одер	му ця рівність не виконується.
жуємо неправильну рівність –4 = 0).
Отже, пара чисел (a, b) = (2; 0) не за
довольняє умові задачі.

Відповідь: (0; 0), (1; 0). Y

20.3. ВИКОРИСТАННЯ УМОВ РОЗМІЩЕННЯ КОРЕНІВ КВАДРАТНОГО ТРИЧЛЕНА f (x) = ax2 + bx + c (a ≠ 0)

ВІДНОСНО ЗАДАНИХ ЧИСЕЛ А і В

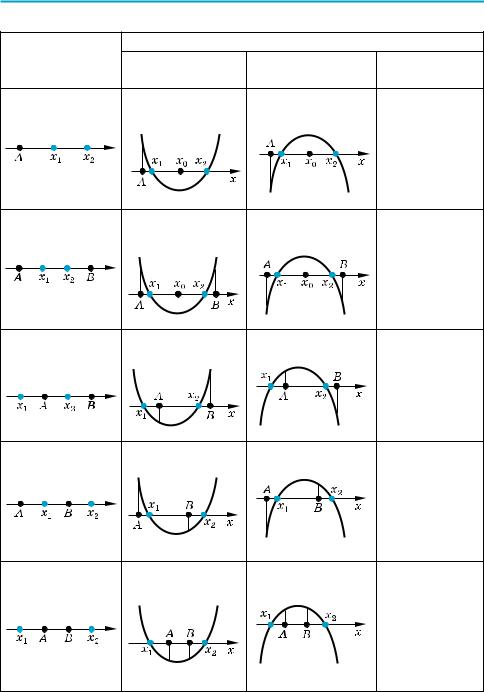
Розв’язування деяких дослідницьких задач з параметрами можна звести до використання необхідних і достатніх умов розміщення коренів квадратно го тричлена. Основні з цих умов наведено в таблиці 37 (у таблиці використано

традиційні позначення x = −

, D = b2

– 4ac).

Т а б л и ц я 37

Розміщення

Необхідні і достатні умови розміщення коренів

у загальному

коренів

при a > 0

при a < 0

випадку (а ≠ 0)

1. x1 < A;

f (A) > 0

f (A) < 0

x2 < A

D l 0; x0 < A;

D l 0; x0

< A;

a f (A) > 0,

Dl 0,

x0 < A

2. x1 < A < x2

f (A) < 0

f (A) > 0

aæf (A) < 0

225

		РОЗДІЛ 2. Тригонометричні рівняння і нерівності
			П р о д о в ж. т а б л. 37
	Розміщення	Необхідні і достатні умови розміщення коренів
	Розміщення			у загальному
	коренів	при a > 0	при a < 0	у загальному
	коренів	при a > 0	при a < 0	випадку (а ≠ 0)
				випадку (а ≠ 0)
3. x1 > A;		f (A) > 0	f (A) < 0
	x2 > A	D l 0; x0 > A;	D l 0; x0 > A;	a f (A) > 0,

				Dl 0,

				x0 > A
4. A < x1 < B;		f (A) > 0; f (B) > 0 f (A) < 0; f (B) < 0		a f (A) > 0,
	A < x2 < B	D l 0; A < x0 < B D l 0; A < x0 < B		a f (A) > 0,
	A < x2 < B	D l 0; A < x0 < B D l 0; A < x0 < B		a f (B) > 0,
				a f (B) > 0,
				Dl 0,
				A < x < B
				0
5.	x1 < A;	f (A) < 0; f (B) > 0 f (A) > 0; f (B) < 0
	A < x2 < B			a f (A) < 0,
				a f (A) < 0,
				a f (B) > 0
6. A < x1 < B;		f (A) > 0; f (B) < 0 f (A) < 0; f (B) > 0
	x2 > B
				a f (A) > 0,
				a f (B) < 0
7. x1 < A;		f (A) < 0; f (B) < 0 f (A) > 0; f (B) > 0
	x2 > B			a f (A) < 0,
				a f (A) < 0,
				a f (B) < 0
			226

§ 20. Тригонометричні рівняння з параметрами

Пояснення й обґрунтування

Для обґрунтування зазначених умов досить скористатися тим, що графік функції f (x) = ax2 + bx + c (a ≠ 0) суцільна (нерозривна*) лінія. Якщо така функція на кінцях якогось проміжку набуває значень з різними знаками (тоб то відповідні точки графіка знаходяться в різних півплощинах відносно осі Оx), то всередині цього проміжку є принаймні одна точка, у якій функція дорівнює нулю (рис. 98).

Наприклад, для того щоб два різні корені квадратного тричлена f (x) = ax2 + bx + c (a ≠ 0) при a > 0 були розміщені по різні боки від заданого числа A, достатньо зафіксувати тільки одну умову f (A) < 0 (рис. 99).

(Дійсно, графік квадратичної функції f (x) = ax2 + bx + c при a > 0 — парабо

ла, вітки якої напрямлено вгору. Тоді у випадку, коли аргумент x прямує

до +× або до –× (це позначається звичайно так: х → +× або х → –×), функція f (x) прямує до +× (f (x) → +×), отже, f (x) > 0 при х → +× або х → –×. Якщо виконується умова f (A) < 0, то при зміні значення аргумен ту x від A до +× квадратична функція f (x) змінює свій знак з «–» на «+»,

отже, f (x) має принаймні один корінь x2 > A.

Так само при зміні значення аргументу x від –× до A квадратична функція

f (x) змінює свій знак з «+» на «–», отже, f (x) має принаймні один корінь x1 < A. Але квадратний тричлен f (x) не може мати більше двох коренів, отже, при a > 0 умова f (A) < 0 необхідна і достатня для того, щоб два різні корені квадратного тричлена знаходилися по різні боки від заданого числа A. )

Аналогічні міркування при a < 0 показують, що для виконання цієї cамої вимоги необхідно і достатньо, щоб f (A) > 0. Ці дві умови можна об’єднати в одну: aæf (A) < 0.

Дійсно, aæf (A) < 0	a > 0,	a < 0,	Отже,
Дійсно, aæf (A) < 0		або	Отже,
	f ( A) < 0	f ( A)	> 0.

квадратний тричлен f (x) = ax2 + bx + c (a ≠ 0) має два різні корені, що

знаходяться по різні боки від заданого числа A тоді і тільки тоді, коли виконується умова aæf (A) < 0.

Рис. 98

Рис. 99

* Більш строго відповідну властивість буде обґрунтовано в 11 класі під час розгляду так званих неперервних функцій.

227

РОЗДІЛ 2. Тригонометричні рівняння і нерівності

Аналогічно обґрунтовуються й інші умови, наведені в таблиці 37. Зауважимо, що наведені умови можна спеціально не запам’ятовувати, а

для їхнього запису користуватися графіком квадратичної функції (зображе ним для потрібного розміщення коренів) і таким о р і є н т и р о м.

Для того щоб корені квадратного тричлена f (x) = ax2 + bx + c (a ≠ 0) були розміщені заданим чином відносно даних чисел A і B, необхідно і достатньо виконання системи умов, яка включає:

1)знак коефіцієнта при старшому члені;

2)знаки значень f (A) і f (B);

3)знак дискримінанта D;

4)положення абсциси вершини параболи (x0 = − 2ba ) відносно даних чисел A і B.

Зазначимо, що для випадків, у яких хоча б одне з даних чисел знаходить ся між коренями квадратного тричлена (див. другий, п’ятий, шостий і сьо мий рядки табл. 37), досить виконання перших двох умов цього орієнтиру, а для інших випадків доводиться розглядати всі чотири умови. Також заува жимо, що, записуючи кожну з указаних умов, слід подивитися, чи буде вико нуватися вимога задачі в тому випадку, якщо в цій умові записати знак не строгої нерівності.

Приклад 1	Знайдіть всі значення параметра a, для яких рівняння
	cos 2x + a sin x – 9 = 0	(1)
	має корені.

К о м е н т а р

Спочатку виконаємо рівносильні перетворення заданого рівняння: зведе мо до одного аргументу і до однієї функції, а потім виконаємо заміну sin x = t. Слід враховувати, що після заміни змінної іноді змінюється вимога задачі, зокрема для рівняння (2) вона буде такою: знайти всі значення параметра a, для яких це рівняння має хоча б один корінь у проміжку [–1;1] (тоді після оберненої заміни ми знайдемо корені рівняння sin x = t, а значить, і корені рівняння (1)). Це можливо в одному з трьох випадків: або обидва корені рівняння (2) знаходяться в цьому проміжку або тільки один з коренів рівнян ня (2) знаходиться в проміжку [–1;1], а другий — праворуч або ліворуч від цього проміжку. Зобразивши відповідні ескізи графіків функції f (t) = 2t2 – at + 8 (див. рисунки), за наведеним орієнтиром (або за таблицею 37) записуємо відповідні достатні умови розміщення коренів (3)–(5). При цьому враховуємо, що у випадках, коли f (–1) = 0 або f (1) = 0, то умова задачі теж виконується.

228

§20. Тригонометричні рівняння з параметрами

Укінці необхідно об’єднати всі отримані результати.

Зазначимо, що для одержання відповіді можна розв’язати рівняння (2):

t	=	a ± a2 − 64	, а потім розв’язати сукупність нерівностей: –1 m t		m 1,
				1
1, 2	4

–1 m t2 m 1, але нерівності з коренями (ірраціональні) буде розглянуто тільки в наступному розділі, та й розв’язувати їх досить складно.

Р о з в ’ я з а н н я

X Задане рівняння рівносильне рівнянням: 1 – 2 sin2 x + a sin x – 9 = 0, 2 sin2 x – a sin x + 8 = 0. Заміна sin x = t дає рівняння

2t2 – at + 8 = 0.

(2)

Рівняння (1) матиме корені тоді і тільки тоді, коли рівняння (2) матиме хоча б один корінь у проміжку [–1;1].

1) Для того щоб обидва корені квадратного тричлена f (t) = 2t2 – at + 8 знахо

	f (−1) l 0,
дилися в цьому проміжку, досить виконання умов	f (1) l 0,
	D l	(3)
		0,
	−1 m t m1.
		0

2) Для того щоб один корінь f (t) знаходився в проміжку [–1;1], а другий —

праворуч від 1 (або в точці 1), досить виконання умов f (−1) l 0,	(4)
f (1) m 0.

3) Для того щоб один корінь f (t) знаходився в проміжку [–1;1], а другий —

ліворуч від –1 (або в точці –1), досить виконання умов f (−1) m 0,										(5)
Розв’язуємо сукупність систем нерівностей (3)–(5):									f (1) l 0.
Розв’язуємо сукупність систем нерівностей (3)–(5):
10 +a l 0,
10 −a l 0,				або	+	a l0,	або	+	a m0,
a2	−64 l 0,			або	+		або	+
				10			10
				10 −a m0			10 −a l 0.
−1 m		a	m1
−1 m			m1
	4
a l −10,
Тоді a m10,			або al−10, або a m −10,
a m −8 або a l 8,				a l10		a m10.
−4 m a m 4

Перша система не має розв’язків, а з інших одержуємо a l 10 або a m –10. Відповідь: a (–×; –10] [10; +×). Y

229

РОЗДІЛ 2. Тригонометричні рівняння і нерівності

	Вправи
	Розв’яжіть рівняння (1–2).
1.	1) a sin x = 1;			2) a sin 2x = cos x;
	3) a tg x = sin x;			4) ctg x = a cos x.
2.	1) cos 2x + 2 sin x + a – 1 = 0;					2) sin 3x – sin 2x = a sin x;
	3)	tg ax	= 0;	4) asinx + tg x + 1 =			1	.

		sin bx					cos x
3.	Знайдіть всі значення параметра, при яких рівняння має корені:
	1) 2 sin x + 4 cos x = a;				2) 3 sin x – 4 cos x = b;
	3) a cos 2x – sin x = 0;				4) cos 2x + a cos x = 0;

5) arcsin2 x + (3a – 3) arcsin x + (a – 2)(5 – 4a) = 0.

4.При яких значеннях параметра а рівняння cos2 2x + (a – 3) cos 2x = 0 має

на відрізку π ; 5π рівно чотири корені?

4 4

5. Знайдіть всі пари чисел (a, b), для яких коренями рівняння

a (cos 3x – 1) + b2 – 2b = cos (3ax + (b – 1)2) – 2 будуть усі дійсні числа.

6. Знайдіть всі значення параметра а, при яких рівняння (4a + 2) sin x +

					5π
+ 2a cos x + a + 1 = 0 має точно один корінь, який належить відрізку 0;					.
7. Розв’яжіть нерівність:					6
7. Розв’яжіть нерівність:
1) 2 sin x > a;	2) (5a – 7) cos x < a + 5;
3) a sin2 x + 2 cos x – a + 1 > 0;	4)	cosx +	1	la.
3) a sin2 x + 2 cos x – a + 1 > 0;	4)	cosx +		la.
			cos x

8.При яких значеннях параметра а задана нерівність виконується при всіх значеннях х?


1) sin6 x + cos6 x + a sin x cos x l 0;													2) sin4 x + cos4 x > 3a sin x cos x.
9. При яких значеннях параметра а задані рівняння рівносильні?
1)	sinx +	1		= 0	і (sinx +	1		)(sinx −	a		)= 0;
									2
	2				2
2)	cosx −		1	= 0	і (cosx −		1	)(cosx +		a − 2		)= 0;

	2				2				2

3) sin 2x + a = sin x + 2a cos x і 2 cos 2x + a2 = 5a cos x – 2.

10.Розв’яжіть систему:

	cosxcos y = a2,
1)		sinx cosy = a,
1)		2)
	sinx siny = 1.	sinycosx = 1.

230

<<< < Предыдущая 11 12 13 14 15 16 17 18 19 20 21 2223 / 4523 24 25 26 27 28 29 30 31 32 33 34 35 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.03.20158.49 Mб8978-966-00-1063-5.pdf
#
07.03.2016315.39 Кб16ADMINISTRATIVNO_PRAVOVIJ_STATUS_MON-2.doc
#
07.03.2016359.42 Кб11AGRARNA_POLITIKA_UTsR_DIPLOMNA_ROBOTA.doc
#
21.11.2019178.18 Кб5Alekhina_glava4-97.doc
#
09.11.20194.5 Mб21Alesinskaya_Reshenie_zadach_Ekonom_metody_model...doc
#
22.03.20155.24 Mб60algebra10_нелін_дворівн.pdf
#
07.03.20161.34 Mб214AMMA.doc
#
12.11.20181.63 Mб22Angl.doc
#
30.04.201517.56 Кб45angl.docx
#
22.03.201533.28 Кб278Annotatsia_proizvedenia_Groza.doc
#
22.03.201545.11 Mб46Antichnaya_mifologia_Entsiklopedia.rtf