algebra10_нелін_дворівн

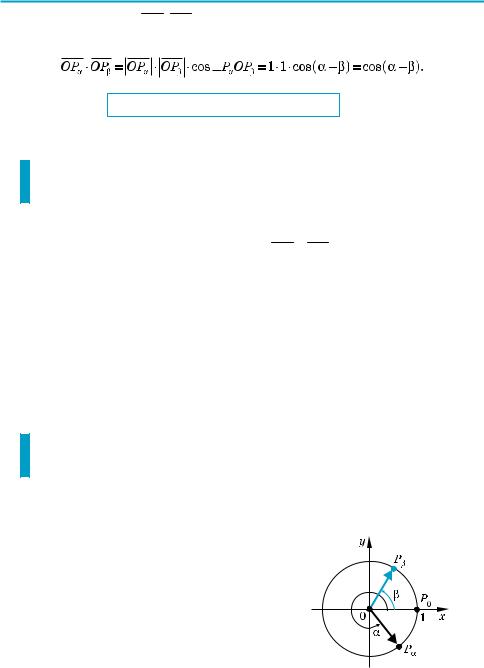
§ 7. Формули додавання та їх наслідки

OPα OPβ = cosα cos β + sinα sin β;

Одержану формулу називають формулою косинуса різниці. Словесно її мож$ на сформулювати так:

косинус різниці двох кутів (чисел) дорівнює добутку косинуса пер шого кута (числа) на косинус другого плюс добуток синуса першого на синус другого.

Щоб обґрунтувати цю формулу в загальному випадку, згадаємо, що за означенням кут між векторами ( РαOРβ) може бути тільки в межах від 0

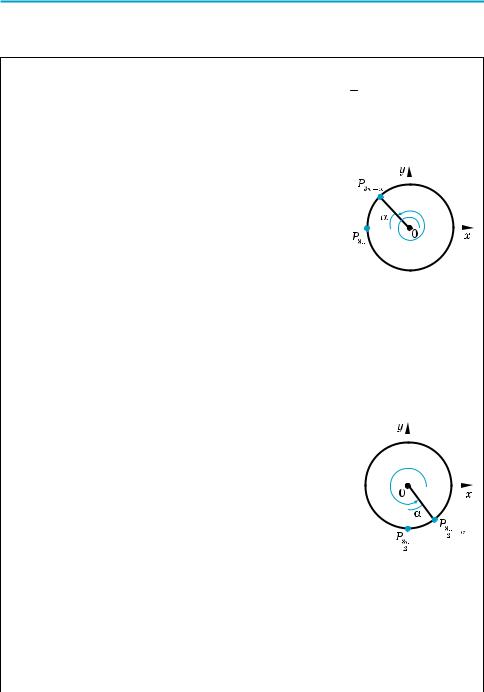
до π, тому при α > β кут між векторами OPα і OPβ може дорівнювати α – β (рис. 71), або може дорівнювати 2π – (α – β) (рис. 72), або може відрізняти$ ся від цих значень на ціле число обертів (тобто на 2πk, де k Z).

Враховуючи періодичність (з періодом 2π) та парність функції косинус, одер$ жуємо, що в будь$якому випадку cos РαOРβ = cos (α – β), отже, наведене обґрунтування залишається правильним для будь$яких значень α і β.

За допомогою формули (1) легко вивести формулу косинуса суми: cos (α + β) = cos (α – (–β)) = cos α cos (–β) + sin α sin (–β) =

= cos α cos β – sin α sin β. Отже,

Косинус суми двох кутів (чисел) дорівнює добутку косинуса першо го кута (числа) на косинус другого мінус добуток синуса першого на синус другого. )

2. Синус суми і різниці.

(Виведемо тепер формули синуса суми і синуса різниці. Спочатку за формулою (1) одержи$

мо два корисні співвідношення. А саме:

= 0 cos ϕ + 1 sin ϕ = sin ϕ. Запишемо одержану формулу спра$ ва наліво:

81

РОЗДІЛ 1. Тригонометричні функції

Cинус суми двох кутів (чисел) дорівнює добутку синуса першого кута (числа) на косинус другого плюс добуток косинуса першого на синус другого.

Для синуса різниці маємо:

sin (α – β) = sin (α + (–β)) = sin α cos (–β) + cos α sin (–β) = = sin α cos β – cos α sin β. Отже,

sin (α – β) = sin α cos β – cos α sin β .

Cинус різниці двох кутів дорівнює добутку синуса першого кута (чис ла) на косинус другого мінус добуток косинуса першого на синус другого. )

3. Тангенс суми і різниці.

(За допомогою формул додавання для синуса (5) і косинуса (2) легко одер$ жати формули додавання для тангенса чи котангенса. Наприклад,

Поділимо чисельник і знаменник останнього дробу на добуток cos α cos β (звичайно, за умови, що cos α ≠ 0 і cos β ≠ 0 ) і одержимо:

82

§ 7. Формули додавання та їх наслідки

Приклади розв’язання завдань

Приклад 1 Обчисліть: 1) sin 15°; 2) cos15°; 3) tg 15°.

cos(α + β ) + sinα sinβ

Приклад 2 Спростіть вираз cos(α − β) − sinα sinβ .

Ко м е н т а р

Учисельнику і знаменнику дробу використаємо формули косинуса суми

ікосинуса різниці та зведемо подібні члени.

Ро з в ’ я з а н н я

Приклад 3 Знайдіть значення виразу cos 37° cos 23° – sin 37° sin 23°.

83

РОЗДІЛ 1. Тригонометричні функції

К о м е н т а р Для обґрунтування цих тотожностей доведемо, що їхні праві частини до$

рівнюють лівим, використовуючи формули синуса суми і синуса різниці: sin (α ä β) = sin α cos β ä cos α sin β.

Запитання для контролю

1.Запишіть формули додавання: а) косинус суми і косинус різниці; б) синус суми і синус різниці; в) тангенс суми і тангенс різниці.

2*. Доведіть формули додавання: а) косинус суми і косинус різниці; б) синус суми і синус різниці; в) тангенс суми і тангенс різниці.

84

§ 7. Формули додавання та їх наслідки

3. За допомогою формул додавання обчисліть:

1) sin 75°; 2) cos 75°; 3) tg 75°; 4) sin 105°; 5) cos 105°; 6) tg 105°.

4.Доведіть тотожність:

1)sin (α + β) + sin (α – β) = 2 sin α cos β;

2)cos (α – β) – cos (α + β) = 2 sin α sin β;

7*) tg(34π − α)+ tg α = tg(34π − α)tg α − 1; 8*) tg(α + 4π )− tg α = 1+ tg(α + 4π )tg α;

7.2. ФОРМУЛИ ПОДВІЙНОГО АРГУМЕНТУ

Т а б л и ц я 16

sin 2α = 2 sin α cos α

cos 2α = cos2 α – sin2 α = 1 – 2 sin2 α = 2 cos2 α – 1

α = 2 tgα

tg2

1 − tg 2α

Пояснення й обґрунтування

(Щоб одержати формули подвійного аргументу, досить у формулах дода$ вання

sin (α + β) = sin α cos β + cos α sin β, cos (α + β) = cos α cos β – sin α sin β,

tg(α + β) = tgα + tgβ 1 − tgα tgβ

взяти β = α. Одержимо тотожності:

sin 2α = sin α cos α + cos α sin α = 2 sin α cos α, тобто sin 2α = 2 sin α cos α.

cos 2α = cos α cos α – sin α sin α = cos2 α – sin2 α, тобто cos 2α = cos2 α – sin2 α.

85

РОЗДІЛ 1. Тригонометричні функції

З формули cos 2α = cos2 α – sin2 α, користуючись основною тригонометрич$ ною тотожністю cos2 α + sin2 α = 1, можна одержати формули, які дозволяють виразити cos 2α тільки через sin α або тільки через cos α.

( Дійсно, з основної тригонометричної тотожності одержуємо sin2 α = 1– cos2 α, cos2 α = 1 – sin2 α. Тоді

cos 2α = cos2 α – sin2 α = cos2 α – (1– cos2 α) = 2 cos2 α – 1, тобто

З формул (1) і (2) можна одержати наслідки, які корисно запам’ятати:

Ці формули називають формулами зниження степеня.

Якщо в останніх формулах позначити 2α = x, тобто α = x , то можна запи$

2

сати такі формули:

Зазначимо, що формули синуса і косинуса подвійного аргументу справед$ ливі для будь$яких значень аргументу, тоді як формула тангенса подвійного аргументу справедлива тільки для тих значень аргументу α, для яких озна$

чені tg α і tg 2α, тобто тільки при α ≠ π + πk і 2α ≠ π + πk, де k Z.

22

Зазначимо також, що, як завжди, одержані формули можна використову$ вати як зліва направо, так і справа наліво. Наприклад, замість виразу 2 sin 3α cos 3α можна записати sin (2æ3α) = sin 6α, а замість виразу cos2 1,5α – sin2 1,5α записати cos 3α.

Приклади розв’язання завдань

86

§ 7. Формули додавання та їх наслідки

К о м е н т а р

Доведемо, що ліва частина тотожності дорівнює правій. Зазначимо, що в чисельнику дробу знаходиться вираз, який можна безпосередньо перетвори$ ти за формулою (3). Але застосування цієї формули зменшує аргумент удвічі: 1 + cos 4α = 2 cos2 2α. Бажано і в знаменнику дробу перейти до того самого аргументу 2α, який з’явився в чисельнику. Для цього розглянемо sin 4α як синус подвійного аргументу (відносно аргументу 2α): sin 4α = sin (2æ2α) = = 2 sin 2α cos 2α.

Р о з в ’ я з а н н я

К о м е н т а р

Перетворюючи тригонометричні вирази, слід пам’ятати не тільки триго$ нометричні, а й алгебраїчні формули. Зокрема, якщо використати в знамен$ нику дробу формулу косинуса подвійного аргументу: cos 2α = сos2 α – sin2 α, одержуємо вираз, який є різницею квадратів сos α та sin α. Його можна роз$ класти на множники як добуток суми та різниці цих виразів. З огляду на вираз, одержаний у знаменнику, у чисельнику розглянемо вираз sin 2α = = 2 sin α cos α як подвоєний добуток sin α на cos α. Тоді для отримання квад$ рата суми цих виразів нам потрібна ще сума sin2 α + сos2 α, але за основною тригонометричною тотожністю цю суму дає одиниця, яка стоїть у чисель$ нику.

Р о з в ’ я з а н н я

87

РОЗДІЛ 1. Тригонометричні функції

Запитання для контролю

1. Запишіть формули синуса, косинуса і тангенса подвійного аргументу. 2*. Доведіть формули синуса, косинуса і тангенса подвійного аргументу.

88

§ 7. Формули додавання та їх наслідки

9*. Знайдіть cos 2α, якщо sinα + 3cos α = 3.

sinα − cos α

10*. Знайдіть найбільше і найменше значення виразу cos 2α – | cos α |.

11. Побудуйте графік функції:

1) y = sin x cos x; 2) y = sin4 x – cos4 x; 3*) y = tg x sin 2x.

89

РОЗДІЛ 1. Тригонометричні функції

7.3. ФОРМУЛИ ЗВЕДЕННЯ

Т а б л и ц я 17

Формулами зведення називають формули, за допомогою яких триго$ нометричні функції від аргументів виду kπ ä α і (2k + 1) π ± α (k Z) зводять

90