
algebra10_нелін_дворівн
.pdf




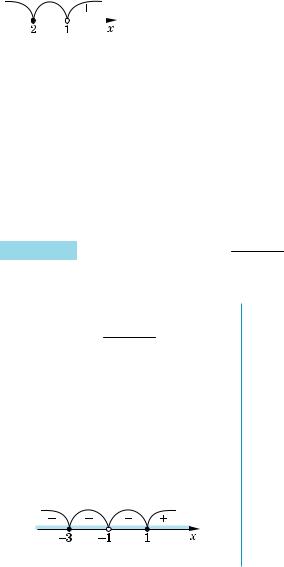

|
|
|
РОЗДІЛ 2. Тригонометричні рівняння і нерівності |
|
|
||||||||
Вправи |
|
|
|
|
|
|
|
|
|
|
|
|
|
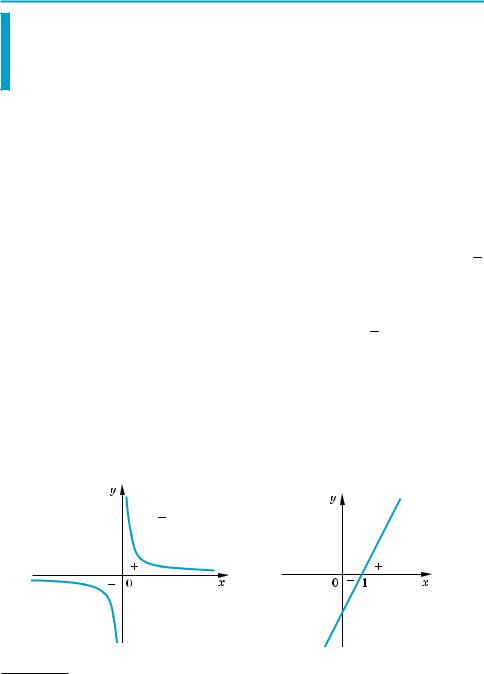
Розв’яжіть нерівність (1–2) двома способами: за допомогою рівносильних |
|||||||||||||
перетворень і за допомогою методу інтервалів. |
|
|
|
|
|||||||||
1. 1) |
x2 − 4 |
l 0; |
2) |
2 |
< |
1 ; |
3) |
x2 − 25 |
m 0; |
4) |
x2 + 12 |
l1. |
|
|
x2 − 3x − |
4 |
|
x + |
2 |
x − 3 |
|
(x + 5)(x − 4) |
|
x2 − 2x − |
8 |
||
2. 1) x4 – 5x2 + 4 m 0; |
|
2) 9x4 – 10x2 + 1 > 0; |
|
|
|
|
|||||||
3) 81x l x3; |
|
|
4) (x2 + 4x – 5)(x2 + 4x + 3) < 105. |
|
|
||||||||
3. Знайдіть область визначення функції: |
|
|
|
|
|||||||||
1) y = |
x − 4 ; 2) |
y = |
2x − x2 − 1 ; |
3) y = 5 − x − 6 ; 4) y = |
x2 − 7x + 12. |
||||||||
|
|
x2 − 4 |
|
x2 + 3x + 2 |
|
|
x |
|
x2 − 2x − 3 |
||||
21.2. РІВНЯННЯ І НЕРІВНОСТІ З МОДУЛЯМИ |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Т а б л и ц я 40 |
|
|
|
|
|
|
|
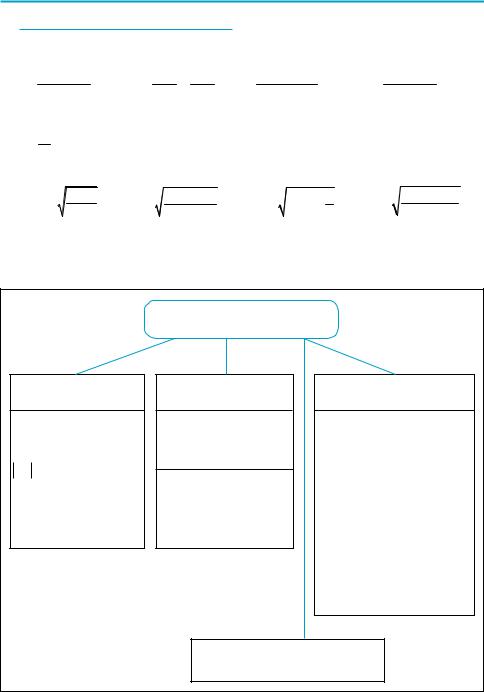
1. Розв’язування рівнянь |
|
|
|
|
|||
|
|
|
|
|
та нерівностей з модулями |
|
|
|
|||||
за означенням |
|
за геометричним |
за загальною схемою |
||||||||||
|
|
|
змістом |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
| a | — відстань на |
1. Знайти ОДЗ. |
|
||||||
|
a, |
якщо a > 0, |
числовій прямій від |
2. Знайти нулі всіх під |
|||||||||
|
точки 0 до точки а. |
модульних функцій. |
|||||||||||
|
|
|
|
|
|||||||||
a |
= 0, якщо a = 0, |
|
1. | f (x) | = a. |
|
3. Позначити нулі на |
||||||||
|
|
|
|
|
|
|
ОДЗ і розбити ОДЗ на |
||||||
|
−a, якщо a < 0. |
|
2. | f (x) | = | g (x) |. |
||||||||||
|
|
|
|
|
|
проміжки. |
|
||||||
|
|
|
|
|
|
3. | f (x) | > a. |
|
4. Знайти |
розв’язок |
||||
|
|
|
|
|
|
4. | f (x) | < a. |
|
у кожному з проміж |
|||||
|
|
|
|
|
|
|
|
|
|
ків (і перевірити, чи |
|||
|
|
|
|
|
|
|
|
|
|
входить цей розв’я |
|||
|
|
|
|
|
|
|
|
|
|
зок у розглянутий |
|||
|
|
|
|
|
|
|
|
|
|
проміжок). |
|
||
|
|
|
|
|
|
|
|
з використанням |
|
|
|
||
|
|
|
|
|
|
|
спеціальних співвідношень |
|
|
||||
|
|
|
|
|
|
|
|
240 |
|
|
|
|
|
