§ 28. Розв’язування ірраціональних рівнянь та нерівностей з параметрами
Р о з в ’ я з а н н я Задана нерівність рівносильна сукупності систем:
x + 1 l 0,
x − a > (x + 1)2
x l− 1,
або
a < −x2 − x − 1
x − a l 0,
або x + 1 < 0. Тоді:
a m x,
x < −1.
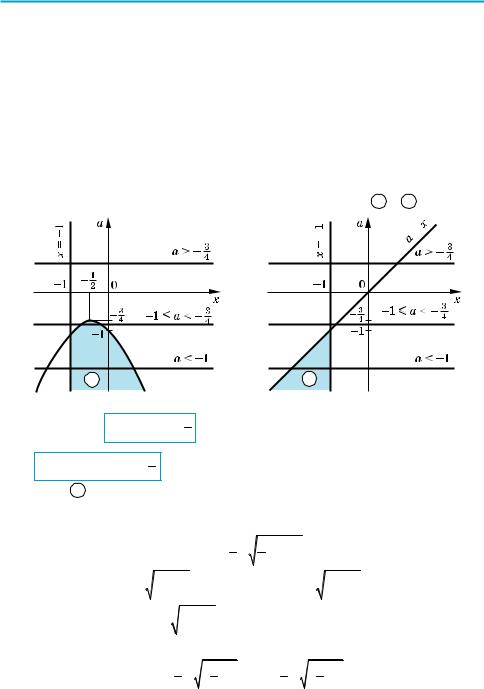
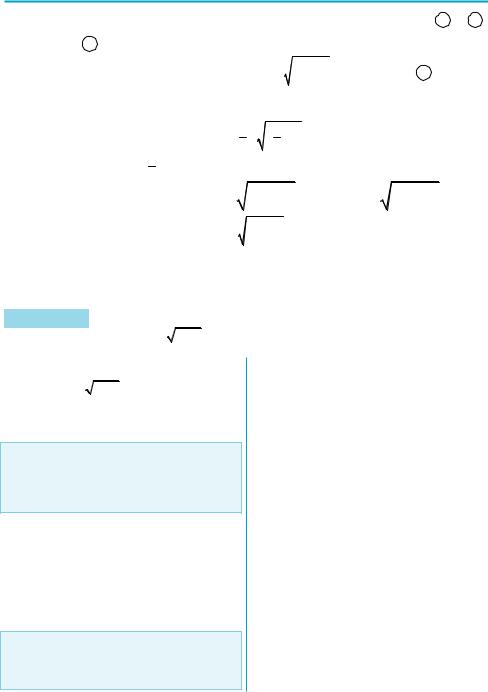
Зобразимо графічно розв’язки систем нерівностей (1) і (2) у системі коор динат xОa (на рисунках заштриховано відповідні області 1 і 2 ).
Бачимо, що: 1) при a l − 3 розв’язків немає (немає заштрихованих то
4
чок); 2) якщо −1ma < − 3 , то пряма a = const перетинає тільки заштрихова
4
ну область 1 . Причому одержаний інтервал обмежений зліва і справа вітка ми параболи а = –х2 – х – 1. Але для відповіді нам потрібно записати х через а. Для цього з рівняння х2 + х + а + 1 = 0 знаходимо х:
x = − 1 ± 1 − a − 1.
24
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Як бачимо, x = − |
1 |
+ |
− |
3 |
− a > − |
1 |
, тобто x = − |
1 |
+ |
− |
3 |
− a — рівняння правої |
|
|
|
|
|
2 |
|
4 |
2 |
2 |
|
4 |
|
вітки параболи, а x = − |
1 |
− |
− |
3 |
− a — лівої. Тоді відповідь у цьому випадку |
|
|
24
буде:
− 1 − − 3 − a < x < − 1 + − 3 − a;
2 4 2 4
РОЗДІЛ 3. Степенева функція
|
|
|
|
|
|
|
3) якщо a < –1 |
, то пряма a = const перетинає заштриховані області 1 і 2 . |
Для області 1 |
інтервал для х обмежений: зліва — прямою х = –1, а справа — |
правою віткою параболи, тобто −1mx < − |
1 |
+ |
− |
3 |
− a. Для області 2 інтервал |
|
|
|
2 |
|
4 |
|
для х обмежений зліва прямою х = а, а справа — прямою х = –1, тобто a mx < –1. Об’єднання цих інтервалів можна коротше записати так:
a mx < − 1 + − 3 − a.
24
Відповідь: 1) при a l − 3 — розв’язків немає;
4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) при −1 ma < − |
3 |
− 1 |
− |
− |
3 |
− a < x < − 1 |
+ |
− |
3 |
− a ; |
|
|
|
|
4 |
2 |
|
4 |
2 |
|
4 |
|
3) при a < –1 a mx < − |
1 |
+ |
− |
3 |
− a. |
|
|
|
|
|
|
|
|
|
|
24
Для розв’язування деяких дослідницьких завдань з параметрами можна використати властивості квадратного тричлена і, зокрема, умови розміщен ня коренів квадратного тричлена відносно заданих чисел (табл. 37, с. 225).
Приклад 6 Знайдіть всі значення параметра k, при яких має корені рівнян ня x + 2k x + 1 − k + 3 = 0.
Р о з в ’ я з а н н я
Заміна x + 1 = t, де t l 0 (тоді x = t2 – 1). Одержуємо рівняння
t2 + 2kt – k + 2 = 0. |
(1) |
Задане рівняння буде мати корені тоді і тільки тоді, коли рівняння (1) буде мати хоча б один невід’ємний ко рінь (t l 0).
Випадок t = 0 дослідимо окремо. При t = 0 з рівняння (1) маємо
k = 2. Отже, при k = 2 рівняння (1) має корінь t = 0. Тоді і задане рівнян ня має корінь x = –1, тобто k = 2 задо вольняє умові задачі.
Позначимо f (t) = t2 + 2kt – k + 2.
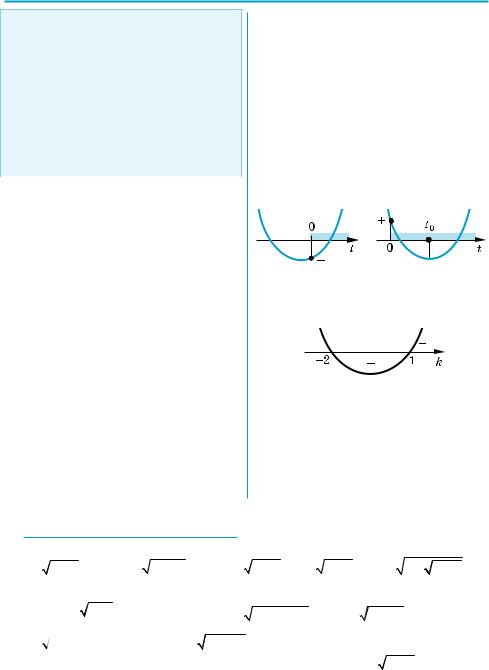
Рівняння (1) може мати хоча б один додатний корінь в одному з двох випадків:
К о м е н т а р
Якщо ірраціональне рівняння містить тільки один корінь, то інко ли можна звести таке рівняння до ра ціонального, позначивши цей корінь новою змінною. Оскільки заміна є рів носильним перетворенням (разом з оберненою заміною), то одержуємо рівняння, рівносильне даному, і тому замість дослідження заданого рівнян ня можна досліджувати одержане.
Але при цьому слід враховувати, що після заміни змінної інколи змі нюється вимога задачі, зокрема, для рівняння (1) вона буде такою: знайти всі значення параметра k, для яких це рівняння має хоча б один невід’ємний корінь (тоді після оберненої заміни ми обов’язково знайдемо корені задано го рівняння). Це можливо в одному
§ 28. Розв’язування ірраціональних рівнянь та нерівностей з параметрами
1)один корінь додатний і один від’ ємний — для цього необхідно і до статньо виконання умови f (0) < 0;
2)обидва корені додатні — для цього необхідно і достатньо виконання системи умов:
|
f (0) > 0, |
|
|
|
(2) |
|
D l 0, |
|
|
|
|
t0 > 0. |
|
Умова f (0) < 0 дає: –k + 2 < 0, |
|
тобто k > 2. |
|
|
Система (2) дає: |
|
−k + |
2 > 0, |
|
|
|
|
4k2 − 4( −k + 2) l 0, |
|
|
|
|
−k > 0. |
|
Тоді: |
|
|
k < 2, |
k < 2, |
|
|
|
|
k2 + k − 2 l 0, k m − 2 або k l1, |
|
|
|
|
k < 0. |
k < 0. |
|
|
Отже, k m –2. |
Відповідь: k m –2 або k l 2.
Вправи
1. Розв’яжіть рівняння:
з трьох випадків: або один з коренів рівняння (1) дорівнює нулю (цей ви падок легко досліджується підстанов кою в рівняння (1) t = 0), або рівняння
(1) має один додатний і один від’ємний корені, або обидва корені додатні. Зоб разивши відповідні ескізи графіків функції f (t) = t2 + 2kt – k + 2 (див. рисунок), записуємо необхідні і дос татні умови такого розміщення для коренів квадратного тричлена (або ви користовуємо табл. 37 на с. 225).
Для розв’язування квадратної не рівності k2 + k – 2 l 0 можна викорис тати графічну ілюстрацію.
У кінці необхідно об’єднати всі одержані результати. Звичайно, для одержання відповіді можна було роз в’язати задане рівняння (аналогічно прикладу 2), а потім дати відповідь на запитання задачі, але такий шлях потребує більш громіздких обчислень.
|
1) |
x − a = 2; 2) x + 2a = a; 3) x + 6 − m = x − 3; 4) a − a + x = x. |
2. |
Розв’яжіть нерівність: |
|
|
|
1) (x − 1) a − x l 0; |
2) x + 2a > 3ax + 4a2 ; |
3) 4x + a > x; |
|
|
2 − x |
|
|
|
4) |
x − a l2x + 1; |
5) a2 − x2 > 2 − x. |
|
3. |
Знайдіть всі значення параметра a, при яких рівняння 3 x + 2 = 2x + a має |
|
корені. |
|
|

РОЗДІЛ 3. Степенева функція
4. |
Знайдіть всі значення параметра a, при яких рівняння ( |
x − a)(x − |
4 |
)= 0 |
|
|
має тільки один дійсний корінь. |
|
x |
|
|
|
|
5. |
Знайдіть всі значення параметра a, при яких рівняння |
2 − ax + 2 = x має |
|
тільки один дійсний корінь. |
|
|
|
|
|
x, |
|
|
y = a + |
залежно від значення |
6. Визначіть кількість розв’язків системи |
|
параметра a. |
2x + y −1 = 0 |
|
|
|
|
ДОДАТКОВІ ВПРАВИ ДО РОЗДІЛУ 3
1. Звільніться від ірраціональності в знаменнику дробу:
1) |
|
|
|
2 |
|
|
|
|
|
; |
|
|
|
|
|
|
|
2) |
|
|
|
|
3 |
|
|
|
; |
|
|
|
|
|
3) |
2 |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) |
|
|
|
|
|
3 |
. |
|
|
|
|
|
|
3 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 + |
2 |
|
|
|
|
|
|
|
|
|
|
2. Обчисліть: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
)2 |
|
|
3 |
( |
|
|
|
|
|
|
|
|
|
)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5 3 + |
|
|
|
|
50 )(5 − |
|
|
24 ) |
|
|
|
|
|
|
|
|
1) |
|
|
|
5 − 2,5 |
|
|
|
− |
|
|
1,5 − |
|
5 |
|
|
− 1; |
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
75 − 5 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
( |
2 − 1,5 |
)2 |
− |
3 (( |
|
− |
2 |
)3 )2 |
|
|
|
|
|
|
|
|
|
|
|
|
4) |
2 6 − |
|
20 |
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
+ 0,75; |
|
|
|
|
|
|
|
2 |
|
|
5 + |
|
24 |
|
|
11+ 2 |
30 . |
|
|
|
Спростіть вираз (3–5). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
+ 2 |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
2 |
|
|
a − |
2 |
|
|
a a + b b |
|
− |
|
|
|
|
|
|
|
|
|
|
a + b |
|
2 |
|
|
|
|
|
3. 1) |
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ab |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
2a |
|
|
|
|
2a + 2 |
|
a − |
|
|
|
|
|
a + |
2 |
|
|
|
a + b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a − b |
|
|
|
|
|
|
|
|
|
x + 1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
− |
|
|
1 |
|
|
|
2 |
|
|
|
|
c − 1 |
− |
|
|
c + |
1 |
|
|
|
|
|
|
|
3) |
|
|
|
: |
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + x + x x2 − x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 c |
|
|
|
c + 1 |
|
|
|
|
|
c − 1 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
3 |
|
+ 1 |
|
−1 |
|
|
|
4 |
|
3 |
+ |
|
|
k |
|
|
|
|
|
|
( |
a + |
|
|
|
|
b |
)2 |
− |
( |
2 |
b |
)2 |
|
|
|
|
|
a − |
|
|
b |
|
|
|
32b b |
|
4. 1) |
k − |
|
|
|
|
k |
|
|
− |
|
|
k |
|
|
; |
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
: |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a − b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k + 1 |
|
|
|
|
|
|
|
|
k − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a + b |
|
|
|
a + b |
|
|
4 |
x |
3 |
− |
4 |
y |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
a |
3 |
+ |
|
|
ab |
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
b |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
|
|
|
|
|
|
|
|
− (4 x + |
4 y ) |
4 |
|
+1 ; |
4) |
|
|
|
|
|
|
|
|
|
− a b − |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
4 b3 + 4 a4b − 4 ab4 − 4 a3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
x − 1 |
|
|
|
|
x |
+ 1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ab |
|
|
|
|
|
|
|
(ab)4 − b2 |
|
|
|
|
|
|
|
|
5. 1) |
|
|
|
|
|
: |
|
|
|
+ |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
2) |
a |
2 |
b |
2 |
|
− |
|
|
|
|
|
|
|
|
|
|
: |
|
; |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1,5 |
|
|
|
|
−0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
a − b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + x2 + 1 |
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a + a 2b 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 |
−1 |
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− c |
−2 |
|
|
|
|
|
1 |
|
|
|
|
|
c |
−2 |
− c |
|
|
|
|
|
2 |
|
−2 |
|
|
2x + x2 y2 |
|
|
|
x |
2 − y2 |
|
|
|
|
|
x − y |
|
|
|
1 |
|
|
|
|
− |
|
2x 2 |
|
+ |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
. |
3) |
|
3x |
|
|
|
|
|
|
|
|
|
|
|
|
1 1 − |
|
|
|
|
|
|
1 ; |
|
4) |
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
− 1 |
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
− |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − x2 y2 |
|
|
|
|
x2 + y2 |
|
|
|
c |
2 |
− c |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
c2 − c |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Додаткові вправи до розділу 3
Розв’яжіть рівняння (6–10):
6. |
1) ( x2 − 7x + 10)2 = 2x2 − 9x + 7; |
2) x2 + x2 − 1 − (x + x2 − 1) = 0; |
|
3) |
(x + 1)(2x + 3) = x + 3; |
4) |
x + 1 |
2x + 3 = x + 3. |
7. |
1) ( 1+ x + 1)( 1+ x + 2x − 5) = x; |
2) |
2x2 + 3x + 2x2 − 3x − 5 = 3x; |
|
3) |
x2 + 3x − 4 = 2x + 2; |
4) |
x2 − 7x + 1 = 2x2 − 15x + 8. |
8. |
1) |
5x + 7 − 3x + 1 = x + 3; |
2) |
2x + 3 + 3x −1 = 5x + 2; |
|
3) |
x + 3 − 4 x − 1 + x + 8 − 6 x − 1 = 1; |
|
|
|
|
|
|
|
|
4) |
x + 11 − 6 x + 2 + x + 18 − 8 x + 2 = 1. |
|
|
|
|
|
|
9. |
1) 3 2x − 8 + 3 x − 8 = 2; |
2) 3 8x + 4 + 3 8x − 4 = 2; |
|
3) |
x + 3 + 3 5 − x = 2; |
4) 3 2 − x = 1− x − 1. |
|
|
|
10. |
1) |
3 x + 3 x − 16 = 3 x − 8; |
2) |
3 x − 1 + 3 x − 2 − 3 2x − 3 = 0; |
|
3) |
x5 x − 1 |
+ |
5 x3 − 1 |
= 16; |
4) |
1 |
+ |
1 |
|
= |
1 |
. |
|
x + 3 x |
x − 3 x |
|
|
|
|
|
|
5 x3 − 1 |
5 x − 1 |
|
|
3 |
|
Розв’яжіть систему рівнянь (11–12).
11. 1) |
|
x + y = 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − y + 2 = 2y − 2; |
|
|
|
7 |
− |
|
4 |
|
= |
5 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
x − 7 |
|
y + 6 |
3 |
|
3) |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
3 |
|
|
13 |
|
|
|
− |
|
|
= |
; |
|
|
|
x − 7 |
|
y + 6 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + y |
+ 4 |
2x − 1 |
= 5, |
|
|
|
12. 1) |
|
|
|
|
|
2x − 1 |
|
x + y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = y + 1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
2x + y − 1 − x + y = 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x + 2y = 4; |
|
|
|
|
|
Розв’яжіть нерівність (13–21). 13. 1) 3x2 + 13 l1− 2x;
3)3x − x2 < 4 − x;
14. 1) x2 + 3x + 2 − x2 − x + 1 < 1;
|
|
|
x + 3y + 1 = 2, |
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x − y |
+ 2 = 7y − 6; |
|
|
|
5 |
|
+ |
|
|
4 |
|
= |
31 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
x − 9 |
|
|
|
y + 9 |
|
|
|
4) |
|
|
3 |
|
|
|
|
2 |
|
|
7 |
|
|
|
|
|
|
+ |
|
|
|
= |
. |
|
|
|
|
x − 9 |
|
|
y + 9 |
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − y |
+ |
|
|
x + y |
= |
10 |
|
|
|
|
|
|
|
, |
2) |
|
|
|
|
|
|
|
|
|
|
x + y |
|
|
|
x − y |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xy − 2x − 2y = 2; |
|
|
|
|
|
|
3 |
x + 2y |
+ |
3 |
x − y + 2 = 3, |
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x + y = 7. |
|
|
|
|
|
|
|
2)x2 + x > 1− 2x;
4)x2 − x − 2 < 2x + 6.
2)3x2 + 5x + 7 − 3x2 + 5x + 2 > 1;

РОЗДІЛ 3. Степенева функція
|
3) |
|
|
|
|
|
x − 7 |
|
|
|
|
|
|
< 0; |
|
|
|
|
|
4) |
|
17 − 15x − 2x2 |
|
|
> 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x2 − 19x + 12 |
|
|
|
|
|
|
|
x + 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15. |
1) |
|
|
x − 2 |
x − 1 + x + 2 x − 1 m2; |
2) |
|
x + 4 x − 4 − x − 4 |
x − 4 l 3; |
|
3) |
|
|
x + 3 > x − 1 + x − 2; |
4) |
|
x + 6 > |
2x − 4 + x + 1. |
16. |
1) |
|
|
|
1 |
− |
1 |
> 1 |
|
− |
1; |
|
|
|
|
|
|
|
2) |
|
|
1 |
− 3 < |
1 − |
1; |
|
|
|
|
|
|
|
|
|
2 |
4 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
x |
|
|
x |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
x |
4 |
|
x |
2 |
|
|
|
|
|
|
|
3) (x − 1) x2 − x − 2 l0; |
4) (x − 3) x2 + x − 2 l 0. |
17. |
1) |
( |
x |
) |
x |
2 |
+ 1 |
|
> x |
2 |
− 1; |
2) (x − 3) x2 + 1 mx2 − 9; |
|
|
|
+ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
|
|
|
6 + x − x2 |
l |
|
6 + x − x2 |
; |
|
4) |
|
12 + x − x2 |
l |
|
12 + x − x2 |
. |
|
|
|
|
|
2x + 5 |
|
|
|
|
|
|
|
|
x + 4 |
|
|
|
|
|
|
x − 11 |
|
|
|
|
|
|
2x − 9 |
|
|
18. |
1) |
|
|
|
51 − 2x − x2 |
|
< 1; |
|
|
|
|
|
|
|
2) |
|
|
2 − x + 4x − 3 |
l 2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
|
|
x + 5 < 1+ −x − 3 + (x + 5)( −x − 3); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) |
|
|
(x − 5)( −x + 7) + 1 > −x + 7 − x − 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19. |
1) |
|
|
x + 6 > x + 1 + |
|
2x − 5; |
2) |
|
x + 3 > |
x −1 + 2x −1; |
|
3) |
|
|
x2 − 8x + 15 + x2 + 2x − 15 > |
4x2 − 18x + 18; |
|
|
|
|
|
|
|
|
|
|
|
|
20. |
1) |
|
(1 − x) |
1 − x + (1 + x) |
1 + x l1; |
2) |
|
|
x |
x + (1 − x) |
|
|
1 − x |
|
> 1; |
|
|
|
4 − 4x2 + 2(1 − x2 ) |
|
|
|
|
x2 − 2(x2 − x) |
x − x2 |
|
|
|
|
|
1 − x2 |
|
|
|
|
|
|
3) |
|
|
|
1 + x |
+ |
|
|
|
|
1 − x |
l0; |
4) |
|
1 |
|
− |
|
2 |
|
|
|
|
|
m 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − x |
|
2 1 + x − 1 |
|
|
|
|
|
|
|
1 − x 1 − 1 + x |
|
|
21. |
1) |
|
|
1 |
|
|
|
− |
|
|
|
1 |
|
|
|
m |
a |
|
(a > 0); |
2) |
|
1 |
|
+ |
|
1 |
|
|
|
l |
a |
. |
|
|
|
|
|
x − 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − 1 |
|
|
|
|
|
|
|
|
|
|
x + 2 |
|
x |
|
|
|
|
|
|
x + 1 |
|
|
x |
|
|
22. |
Розв’яжіть нерівність |
|
1 − x2 l |
4 |
(x − a) при а = 0 і переконайтеся, що мно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жиною її розв’язків є відрізок. При яких значеннях а множиною розв’язків данної нерівності є відрізок довжиною 59 ?
23.При яких значення параметра а множина розв’язків нерівності a + x2 + ax l x не перетинається з проміжком [–1; 0]?
24.При яких значення параметра а у множині розв’язків нерівності x + x2 − 2ax > 1 міститься проміжок 14 ; 1 ?
ВІДОМОСТІ З ІСТОРІЇ
Поняття степеня виникло в давнину. Збереглися глиняні плитки древніх вавилонян (близько 1700 р. до н. е.), які містять записи таблиць квадратів і кубів та їх обернених значень. До множення рівних множників приводить розв’язування багатьох задач. Вираз квадрат числа виник внаслідок обчис лення площі квадрата, а куб числа — внаслідок знаходження об’єму куба. Але сучасні позначення (типу а4, а5) введені в XVII ст. Р. Д е к а р т о м (1596— 1650).
Дробові показники степеня і найпростіші правила дій над степенями з дро бовими показниками зустрічаються в XIV ст. у французького математика Н. О р е м а (бл. 1323—1382). Відомо, що Н. Ш ю к е (бл. 1445—бл. 1500) розглядав степені з від’ємними і нульовим показниками.
1
С. С т е в і н запропонував розуміти під an корінь n a . Але систематично дробові і від’ємні показники першим став застосовувати Ньютон.
Німецький математик М. Ш т і ф е л ь (1487—1567) дав позначення а0 =1, якщо a ≠ 1, і ввів назву показник (це переклад з німецької Ехроnеnt). Німець ке potenzieren означає піднести до степеня. (Звідси походить і слово потен ціювати, яке буде застосовуватися в наступному розділі для позначення пе реходів від так званих логарифмів (log) виразів f (x) і g (x) до відповідних сте
пенів, тобто від рівності loga f(x) = loga g(x) до рівності aloga f (x) = aloga g (x) . У свою
чергу, термін eхроnеnten виник внаслідок не зовсім точного перекладу з грецької слова, яким Д і о ф а н т А л е к с а н д р і й с ь к и й (близько ІІІ ст.) позначав квадрат невідомої величини.
Терміни радикал і корінь, уведені в XII ст., походять від латинського radix, що має два значення: сторона і корінь. Грецькі математики замість «добути корінь» казали «знайти сторону квадрата за його даною величиною (пло щею)». Знак кореня у вигляді символу 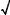 з’явився вперше в 1525 р. Сучас ний символ введений Декартом, який додав горизонтальну риску. І. Н ь ю т о н (1643—1727) вже позначав показники коренів: 3 , 4 .
з’явився вперше в 1525 р. Сучас ний символ введений Декартом, який додав горизонтальну риску. І. Н ь ю т о н (1643—1727) вже позначав показники коренів: 3 , 4 .
Термін логарифм походить від сполучення грецьких слів «логос» (у зна ченні «відношення») і «аритмос» (число) і перекладається як відношення чисел. Вибір винахідником логарифмів Дж. Непером такої назви (1594 р.) пояснюється тим, що логарифми виникли внаслідок зіставлення двох чисел, одне з яких є членом арифметичної прогресії, а друге — геометричної. Лога рифми з основою e увів С п е й д е л (1619 р.), який склав перші таблиці для функції ln х. Назву натуральний (природний) для цього логарифма запропо нував Н. М е р к а т о р (1620—1687), який виявив, що ln х — це площа під
гіперболою y = 1 .
x
327
Рис. 118
§29. Показникова функція, її властивості та графік
Пр о д о в ж. т а б л. 49
6.Проміжки знакосталості: у > 0 при всіх значеннях x R .
7.Найбільшого і найменшого значень функція не має .
8.Для будь!яких дійсних значень u і v (a > 0, b > 0) виконуються рівності:
|
|
|
|
|
|
|
|
аuæаv = аu + v |
|
au |
= au−v |
(au)v = auv |
|
av |
|
|
|
|
|
(ab)u = aubu |
( |
a |
)u = |
au |
|
b |
bu |
|
Пояснення й обґрунтування
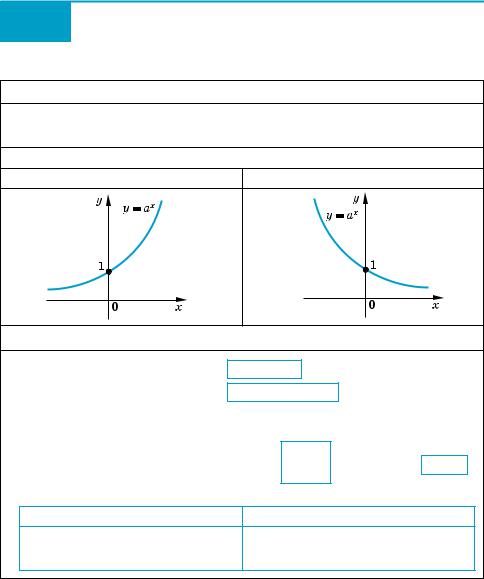
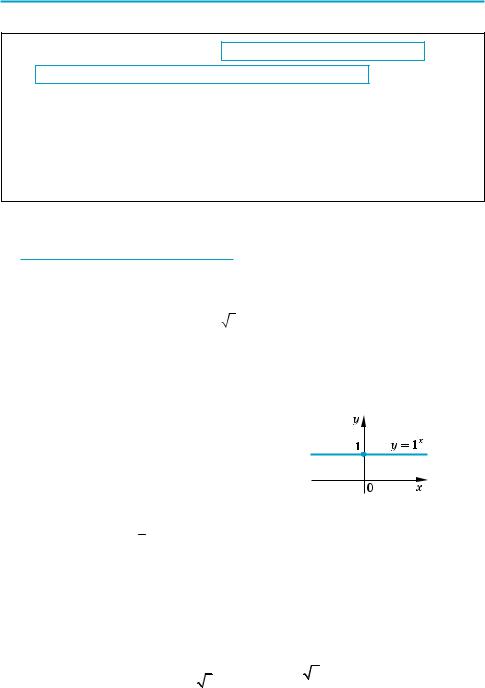
1.Поняття показникової функції та її графік. Показниковою функцією на! зивається функція виду y = ax, де а > 0 і а ≠ 1.
|
|
1 |
x |
|
3 |
x |
|
|
Наприклад, y = 2x, y = ( |
) |
, y = |
|
, y = πx — показникові функції. |
|
|
2 |
|
2 |
|
|
|
|
Зазначимо, що функція виду y = аx існує й при а = 1.
Тоді y = ax = 1x, тобто у = 1 при всіх значеннях x R . Але в цьому випадку функція y = 1x не називається показниковою. (Графік функції y = 1x — пряма, зображена на рисунку 118.)
Оскільки при а > 0 вираз ax означе&
ний при всіх дійсних значеннях x, то об! ластю визначення показникової функції
y = ax є всі дійсні числа.
Спробуємо спочатку побудувати гра& фіки деяких показникових функцій, на&
приклад, y = 2x і y = (12 )x «за точками»,
а потім перейдемо до характеристики загальних властивостей показникової функції.
Складемо таблицю деяких значень функції у = 2х.
x |
–3 |
–2 |
–1 |
|
|
− |
1 |
|
0 |
|
1 |
|
1 |
2 |
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у = 2х |
1 |
|
1 |
|
1 |
1 |
|
≈ 0,7 |
1 |
2 ≈ 1,4 |
2 |
4 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
4 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
РОЗДІЛ 4. Показникова і логарифмічна функції |
а |
б |
|
Рис. 119 |
Побудуємо на координатній площині відповідні точки (рис. 119, а) і з’єднає& мо ці точки плавною лінією, яку природно вважати графіком функції у = 2х (рис. 119, б).
Як бачимо з графіка, функція у = 2х є зростаючою функцією, яка набуває всіх значень із проміжку (0; +×).
Аналогічно складемо таблицю деяких значень функції y = (12 )x .
x |
|
–3 |
–2 |
–1 |
− |
1 |
|
0 |
|
|
|
1 |
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
8 |
4 |
2 |
|
≈ |
|
|
1 |
|
1 |
|
≈ 0,7 |
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = (2 ) |
2 |
1,4 |
2 |
|
2 |
|
4 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Побудуємо на координатній площині відповідні точки (рис. 120, а) і з’єдна& ємо ці точки плавною лінією, яку природно вважати графіком функції y = (12 )x





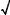 з’явився вперше в 1525 р. Сучас ний символ введений Декартом, який додав горизонтальну риску. І. Н ь ю т о н (1643—1727) вже позначав показники коренів: 3 , 4 .
з’явився вперше в 1525 р. Сучас ний символ введений Декартом, який додав горизонтальну риску. І. Н ь ю т о н (1643—1727) вже позначав показники коренів: 3 , 4 .