
algebra10_нелін_дворівн
.pdf
§ 12. Обернена функція
П р о д о в ж. т а б л. 25
3. Практичний прийом знаходження формули функції, оберненої до функції y = f (x)
|
Алгоритм |
Приклад |
|||||
|
|
|
|
|
|
|
|
1. |
З’ясувати, чи буде функція |
Знайдіть функцію, обернену до |
|||||
|
y = f (x) оборотною на всій об |
функції y = 2x + 4. |
|||||
|
ласті визначення: для цього до$ |
X З рівності y = 2x + 4 можна |
|||||
|
сить з’ясувати, чи має рівняння |
однозначно виразити x через y: |
|||||
|
y = f (x) єдиний корінь відносно |
x = |
1 |
y − 2. |
|||
|
змінної x. |
||||||
|
|
||||||
|
Якщо ні, то виділити (якщо мож |
2 |
|
|
|
||
|
Ця формула задає обернену функ$ |
||||||
|
ливо) проміжок, де існує оберне |
||||||
|
цію, але в ній аргумент позначено |
||||||
|
на функція (наприклад, це може |
||||||
|
через y, а функцію — через x. |
||||||
|
бути проміжок, де функція |
||||||
|
Позначимо в одержаній форму$ |
||||||
|
y = f (x) зростає або спадає). |
||||||
|
лі аргумент через x, а функцію — |
||||||
2. |
З рівності y = f (x) виразити x че |
||||||
через y. |
|||||||
|
рез y. |
||||||
|
|
|
|
|
|
||
3. |
В одержаній формулі ввести тра |
Маємо функцію y = |
1 |
x − 2 , |
|||
|
диційні позначення — аргумент |
|
|||||
|
2 |
|
|||||
|
позначити через x, а функцію — |
обернену до функції y = 2x + 4. Y |
|||||
|
через y. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пояснення й обґрунтування
1. Поняття оберненої функції. Відомо, що залежність шляху від часу руху
тіла, яке рухається рівномірно з постійною швидкістю v0 , виражається фор$ мулою S = v0t. З цієї формули можна знайти обернену залежність — часу
від пройденого шляху t = S . Функцію t(S) = S називають оберненою до функ%
v0 v0
ції S (t) = v0t. Зазначимо, що в розглянутому прикладі кожному значенню t (t l 0) відповідає єдине значення S, і, навпаки, кожному значенню S (S l 0) відповідає єдине значення t.
Розглянемо процедуру одержання оберненої функції в загальному вигляді. Нехай функція f (x) набуває кожного свого значення в єдиній точці її об$ ласті визначення (така функція називається оборотною). Тоді для кожного числа у0 = b (з області значень функції f (x)) існує єдине значення х0 = a, таке, що f (a) = b. Розглянемо нову функцію g (x), яка кожному числу b з області значень функції f (x) ставить у відповідність число a, тобто g (b) = a для кож$ ного b з області значень функції f (x). У цьому випадку функція g (x) нази$
141
РОЗДІЛ 2. Тригонометричні рівняння і нерівності
Рис. 84 |
вається оберненою до функції f (x), а функція f (x) — оберненою до функції
g(x).
Зозначення оберненої функції ви$ пливає, що область значень прямої функції E (f) є областю визначення оберненої функції D (g), а область ви$ значення прямої функції D (f) є облас$ тю значень оберненої функції E (g).
Тобто:
E (f) = D (g), D (f) = E (g).
2.Властивості оберненої функції.
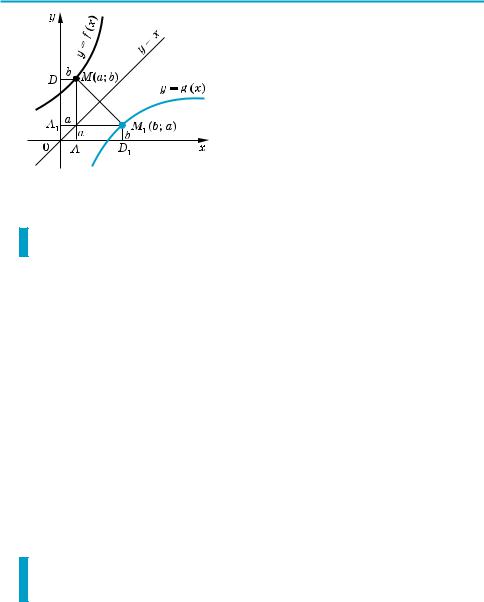
Вл а с т и в і с т ь 1. Графіки прямої і оберненої функції симетричні
відносно прямої у = х.
(Враховуючи наведену вище процедуру побудови функції, оберненої до функції у =f (x), маємо: якщо f (a) = b, то за означенням графіка функції точка M з координатами (a; b) належить графіку функції y = f (x). Анало%
гічно, оскільки g (b) = a, то точка M1 з координатами (b; a) належить гра$ фіку функції y = g (x). Точки M (a; b) і M1 (b; a) розміщені на координатній площині симетрично відносно прямої y = x (рис. 84).
Дійсно, пряма y = x є віссю симетрії системи координат. Отже, при симетрії відносно прямої y = x вісь Оx відображається на вісь Оy, а вісь Оy — на вісь Оx. Тоді (наприклад, при a > 0 і b > 0) прямокутник OAMD із сторонами
OA = a і OD = b на осях координат відображається на прямокутник OA1M1D1 із сторонами на осях координат, у якого OA1 = OA = a і OD1 = OD = b. Таким чином, при симетрії відносно прямої y = x точка M (a; b) відображається в
точку M1 (b; a) (а точка M1 — у точку M). Отже, при симетрії відносно прямої y = x будь$яка точка M (a; b), що належить графіку функції y = f (x), має
відповідну точку M1 (b; a), що належить графіку функції y = g (x), а будь$ яка точка M1 (b; a), що належить графіку функції y = g (x), має відповідну точку M (a; b), що належить графіку функції y = f (x). Тобто графіки взаєм$ но обернених функцій симетричні відносно прямої y = x. )
Вл а с т и в і с т ь 2. Якщо функція f (x) зростає (спадає) на деякому
проміжку, то вона має обернену функцію на цьому проміжку, яка зростає, якщо f (x) зростає, і спадає, якщо f (x) спадає.
(Дійсно, якщо функція f (x) зростає (спадає) на деякому проміжку, то за властивістю зростаючої (спадної) функції кожного свого значення вона набуває в єдиній точці з цього проміжку (с. 14), отже, вона має обернену функцію g (x) на цьому проміжку. Обґрунтувати, що функція g (x) зрос$ тає, якщо f (x) зростає, можна методом від супротивного.
142

§ 12. Обернена функція
Нехай числа а1 і а2 входять до області визначення функції f (x) і |
|
а2 > а1. |
(1) |
Позначимо f (а1) = b1, f (а2) = b2. Якщо функція f (x) зростає, то f (а2) > f (а1), тобто b2 > b1. За означенням оберненої функції g (x) числа b1 і b2 входять до
її області визначення і
g (b1) = а1, g (b2) = а2. |
(2) |
Якщо припустити, що функція g (x) не є зростаючою, то з нерівності b2 > b1 не може випливати нерівність g (b2) > g (b1) (інакше функція g (x) буде зрос$ таючою), отже, може виконуватися тільки нерівність g (b2) m g (b1). Але тоді за формулами (2) одержуємо a2 m a1, що суперечить умові (1). Отже, наше припущення неправильне, і функція g (x) зростає, якщо f (x) зростає.
Аналогічно обґрунтовується, що у випадку, коли функція f (x) спадає, обернена до неї функція g (x) теж спадає. )
3. Практичний прийом знаходження формули функції, оберненої до функції y = f (x). З означення оберненої функції випливає, що для отримання оберне$ ної залежності необхідно знати, як значення x виражається через значення y. Це можна зробити, розв’язавши рівняння y = f (x) відносно змінної x. Якщо задана функція оборотна, то рівняння матиме єдиний розв’язок для всіх y з області значень функції f (x), і ми одержимо формулу x = g (y), яка задає обернену функцію. Але в цій формулі аргумент позначено через y, а функ$ цію — через x. Якщо поміняти позначення на традиційні, то одержимо запис функції, оберненої до функції y = f (x).
Ці міркування разом із відповідним алгоритмом наведено в таблиці 25 і реа$ лізовано в наступних прикладах.
Приклади розв’язування завдань
Приклад 1 Знайдіть функцію, обернену до функції y = 1 .
x − 1
Р о з в ’ я з а н н я
X Область визначення: х ≠ 1. Тоді
з рівності y = 1 маємо
x − 1
ху – у = 1, ху = у + 1, x = y + 1.
y
Позначаємо аргумент через x, а функцію — черезy іодержуємофунк$
цію y = x x+ 1 , обернену до заданої. Y
К о м е н т а р
На всій області визначення (х ≠ 1) задана функція оборотна, оскільки
з рівняння y = |
1 |
можна однознач$ |
|
||
|
x − 1 |
|
но виразити x через y (у ≠ 0 на області значень заданої функції). Одержана
формула x = y + 1 задає обернену фун$
y
кцію, але в ній аргумент позначено через y, а функцію — через x. Зміню$ ючи позначення на традиційні, одер$ жуємо кінцевий результат.
143
РОЗДІЛ 2. Тригонометричні рівняння і нерівності
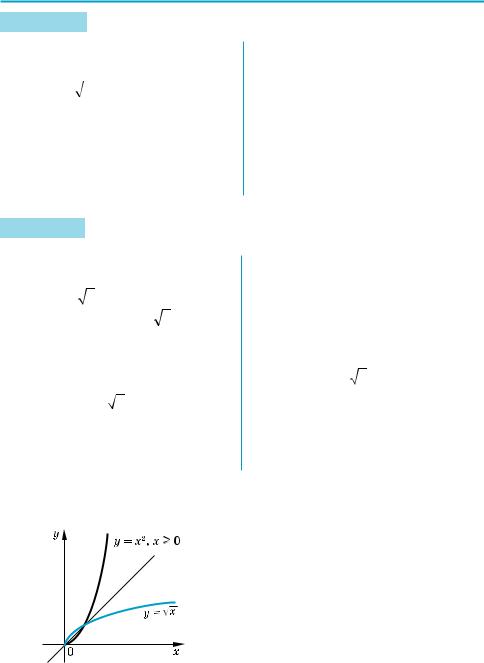
Приклад 2 Знайдіть функцію, обернену до функції y = х2.
Р о з в ’ я з а н н я
X З рівності y = х2 при y l 0 одер$ жуємо x = ± y. Тоді при y > 0 одному значенню y відповідають два значен$ ня x. Отже, на всій області визначен$ ня x (–×; +×) функція y = x2 не є оборотною, і для неї не можна знайти обернену функцію. Y
К о м е н т а р
Область значень заданої функції: y l 0. Але при y > 0 з рівності y = x2 не можна однозначно виразити x че$ рез y. Наприклад, при y = 4 одержує$ мо x = ä2. Через це ми не можемо зна$ ченню y = 4 поставити у відповідність єдине число, щоб побудувати оберне$ ну функцію.
Приклад 3 Знайдіть функцію, обернену до функції y = х2 при x l 0.
Р о з в ’ я з а н н я
X З рівності y = х2 при y l 0 одер$ жуємо x = ± y. Враховуючи, що за умовою x l 0, маємо x = y.
Позначимо аргумент через x, а функцію — через y і одержимо, що функцією, оберненою до функції y = х2, яка задана тільки при x l 0,
буде функція y = x. Y
К о м е н т а р
Множина значень заданої функції: y l 0. При x l 0 задана функція y = х2 зростає, отже, на проміжку x l 0 вона має обернену функцію, а значить, на цьому проміжку рівняння х2 = y ми зможемо однозначно розв’язати: при
x l 0 маємо x = y.
Ця формула задає обернену функ$ цію, але в ній аргумент позначено че$ рез y, а функцію — через x. Замінюю$ чи позначення на традиційні, одер$ жуємо кінцевий результат.
Рис. 85 |
З а у в а ж е н н я. У прикладах 2 і 3 ми фактично розглядаємо різні функ$ ції (вони мають різні області визна$ чення), хоча в обох випадках ці функ$ ції задаються однією і тією самою фор$ мулою. Як відомо, графіком функції y = х2 (приклад 2) є парабола, а гра$ фіком функції y = х2 при x l 0 (при$ клад 3) є тільки права вітка цієї па$ раболи (рис. 85).
144
§ 12. Обернена функція
Запитання для контролю
1.За якої умови для заданої функції y = f (x) можна побудувати обернену функцію?
2.Поясніть побудову графіка оберненої функції на прикладі функції y = f (x), яка задана таблицею:
x |
0 |
2 |
4 |
6 |
|
|
|
|
|
f (x) |
1 |
3 |
5 |
7 |
|
|
|
|
|
Задайте обернену функцію y = g (x) за допомогою таблиці:
x
g(x)
3.Як розміщено графіки прямої і оберненої функцій, якщо вони побудовані
водній системі координат? Проілюструйте відповідну властивість графіків на прикладі.
4*. Обґрунтуйте взаємне розміщення графіків прямої і оберненої функцій.
5.Чи існує обернена функція до функції y = x2, де x m0? Поясніть це, спираю$ чись на відповідні властивості оберненої функції. Якщо обернена функція існує, то задайте її формулою виду y = g (x).
Вправи
1.Запишіть формулу, яка задає функцію y = g (x), обернену до заданої. Укажіть область визначення і множину значень функції g (x):
1°) y = 3x – 6; 2°) y = – 3x – 6; 3) |
y = |
2 |
; |
4) |
y = − |
1 |
; |
5) y = x. |
|
x |
x |
||||||||
|
|
|
|
|
|
|
2.На одному рисунку побудуйте графік даної функції і функції, оберненої до даної:
1°) y = 2x; 2°) y = x – 2; 3) y = − |
1 |
; |
4*) y = |
1 |
; 5*) y = x + 1. |
x |
|
||||
|
|
|
x − 1 |
||
3.Знайдіть функцію, обернену до даної на заданому проміжку, і побудуйте на одному рисунку графік даної функції і функції, оберненої до неї:
1) y = |
1 |
x2 при x l 0; |
2) y = |
1 |
x2 при x m 0; |
4 |
4 |
|
|||
3) y = (x – 2)2 при x l 2; |
4) y = x2 – 2 при x m 0. |
||||
145
§13 ОБЕРНЕНІ ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ
Для одержання обернених тригонометричних функцій для кожної триго$ нометричної функції виділяється проміжок, на якому вона зростає (або спа$ дає). Для позначення обернених тригонометричних функцій перед відповід$ ною функцією ставиться буквосполучення «arc» (читається: «арк»).
13.1. ФУНКЦІЯ y = arcsin x
|
Т а б л и ц я 26 |
|
|
|
1. Графік |
|
|
y = sin x |
y = arcsin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На проміжку |
|
|
|
π sin x зростає. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
− |
π |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Значення arcsin a (| a | m 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
Орієнтир |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приклад |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
arcsin а — це таке число з проміжку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
π |
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
arcsin |
|
|
|
|
3 |
= |
, оскільки |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
− |
|
; |
|
, синус якого дорівнює а. |
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
π |
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
π |
|
3 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
; |
π |
|
|
|
|
− |
|
|
|
; |
|
|
|
|
і sin |
|
= |
|
|
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
− |
2 |
, |
|
|
3 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
2 |
|
|||||||||
|
|
arcsin a = ϕ, якщо |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ = a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Непарність функції y = arcsin x
arcsin (–a) = –arcsin a
146
§ 13. Обернені тригонометричні функції
Пояснення й обґрунтування
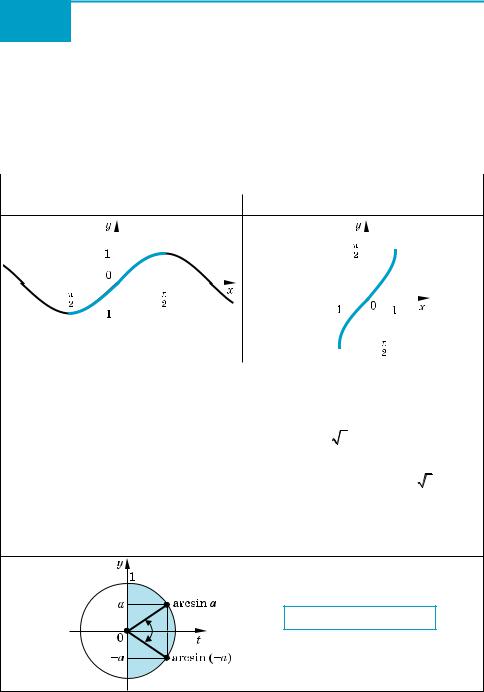
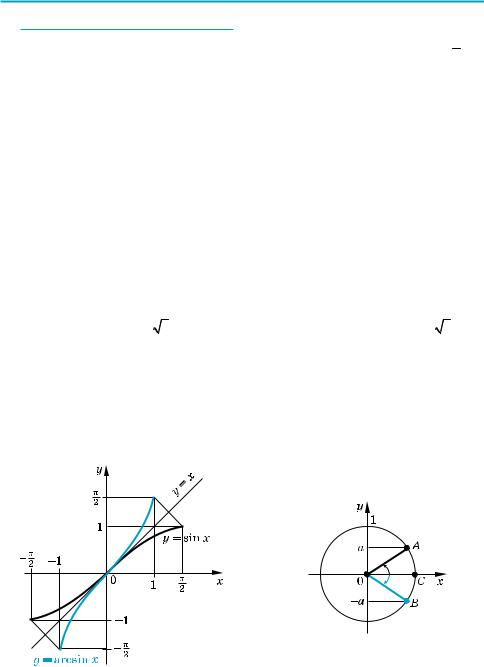
1. Графік функції y = arcsin x. Функція y = sin x зростає на проміжку − π ; π
2 2
і набуває всіх значень від –1 до 1. Отже, на цьому проміжку функція y = sin x має обернену функцію, яка позначається y = arcsin x, з областю визначення
[– 1; 1] і областю значень − π ; π . Функція y = arcsin x теж зростає, і її графік
2 2
можна одержати з графіка функції y = sin x (на заданому проміжку) за допомо$ гою симетричного відображення відносно прямої y = x (рис. 86).
2. Значення arcsin a. За означенням оберненої функції (на вибраному про$
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
π |
|
|
|
|
||
міжку), якщо sin ϕ = a, то arcsin a = ϕ, причому |
|
ϕ − |
|
|
; |
|
і | a | m 1. Отже, |
||||||||||||||||||||||||||||||||||
|
|
2 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
запис arcsin a = ϕ (| a | m 1) означає, що ϕ − |
|
|
|
; |
|
|
|
|
|
і sin ϕ = a, тобто |
|
|
|||||||||||||||||||||||||||||
2 |
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
arcsin a — це таке число з проміжку |
− π ; π |
|
, |
синус якого дорівнює a. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
|
π |
|
|
|
|
|
π |
|
π |
|
|
|
π |
|
|
|
|
|
|
π |
|
|
1 |
|
|
|
|
|
|
|||||||
Наприклад, arcsin |
|
= |
|
, |
оскільки |
|
− |
|
|
; |
|
|
|
|
|
і sin |
|
|
= |
|
|
. |
|
|
|
|
|
||||||||||||||
2 |
6 |
6 |
2 |
|
|
|
|
6 |
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
)= − |
|
|
||||||||||||
|
|
|
|
|
3 |
|
|
|
π |
|
|
|
− |
π |
|
|
− |
π |
|
π |
|
і sin(− |
π |
3 |
|
||||||||||||||||
Аналогічно arcsin − |
|
|
|
|
= − |
|
, оскільки |
3 |
|
|
; |
|
|
|
|
|
. |
||||||||||||||||||||||||
|
|
|
3 |
|
|
|
3 |
2 |
|||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
||||||||||||||
3. Непарність функції y = arcsin x. Для знаходження арксинусів від’ємних чисел можна також користуватися непарністю функції arcsin x, тобто форму$ лою: arcsin (–a) = –arcsin a.
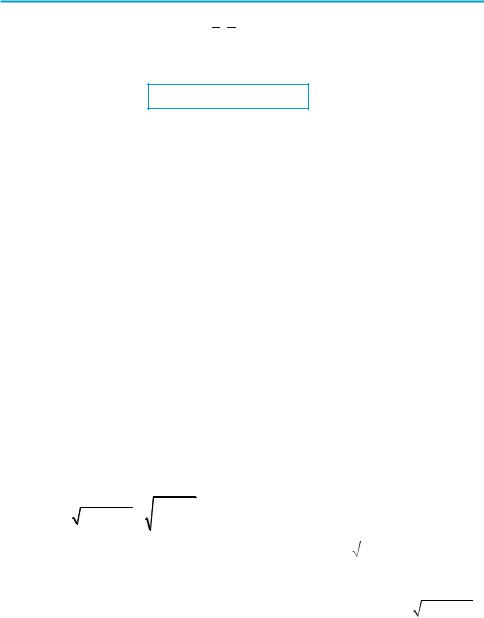
(Це випливає з того, що графік функції y = arcsin x (рис. 86) симетричний відносно початку координат, а також з того, що точки a і (–a) на осі Оy (рис. 87) симетричні відносно осі Оx. Тоді і відповідні точки A і B на оди$
Рис. 86 |
Рис. 87 |
147
РОЗДІЛ 2. Тригонометричні рівняння і нерівності
ничному колі (у проміжку − 2π ; 2π ) теж будуть симетричними відносно осі Оx. Отже, COA = COB. Але arcsin a = COA, а arcsin (–a) = – COB (рисунок 87 наведено для випадку а > 0). Одержуємо
arcsin (–a) = –arcsin a . )
Наприклад, arcsin(− |
1 |
)= −arcsin |
1 |
= − |
π |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) sin(arcsin |
1 |
); |
|
|
cos(arcsin |
3 |
). |
|
|
|
|
|
|||||||||||||||
Приклад |
Знайдіть: |
|
|
2*) |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
Р о з в ’ я з а н н я |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К о м е н т а р |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
1) X Нехай arcsin |
1 |
|
= ϕ, тоді за озна$ |
|
1) Оскільки запис ϕ = arcsin a (| a | m1) |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
||||||||
ченням арксинуса одержуємо, що |
|
|
|
|
|
|
|
|
|
|
π |
|
|||||||||||||||||||||||||||||||||||
|
|
|
означає, що ϕ − |
|
; |
|
і sin ϕ = a, |
||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||
|
|
|
|
|
sinϕ = |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то завжди виконується рівність |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Отже, sin(arcsin |
|
|
|
3)= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
1 |
1 |
. Y |
|
|
|
|
|
|
|
|
|
|
|
sin (arcsin a) = a, | a | m 1 |
. |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Але цю формулу можна не запа$ |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
м’ятовувати: досить позначити |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вираз у дужках через ϕ і викорис% |
|||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тати означення арксинуса. |
||||||||||||||||
2) X Нехай arcsin |
= ϕ. За означен$ |
|
2) Якщо позначити вираз у дужках |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
через ϕ, то за вимогою задачі по$ |
|||||||||||||||||||
ням арксинуса одержуємо, що |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
трібно знайти cos ϕ. Використав$ |
||||||||||||||||||||||||||||||||||||||||||||
|
|
π |
|
π |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ши означення арксинуса, одер$ |
||||||||||||||||||||||||
ϕ |
− |
; |
і sinϕ = |
|
|
. Враховую$ |
|
|
|
жуємо стандартну задачу: знаючи |
|||||||||||||||||||||||||||||||||||||
|
|
5 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
чи, що cos ϕ l 0, маємо: |
|
|
|
|
|
|
|
|
|
синус кута, знайти його косинус, |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1− ( |
|
)2 |
|
|
|
|
|
|
|
|
|
якщо кут знаходиться в проміжку |
|||||||||||||||||
cosϕ = |
|
1− sin2 ϕ = |
|
|
3 |
= |
4 |
. |
|
|
|
|
|
|
|
− π |
π |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
5 |
|
|
|
|
|
|
|
2 ; |
2 . |
|
|
|
|
|
|
|
|
|||||||||
Отже, cos(arcsin |
3 |
)= cosϕ = |
4 |
. Y |
|
|
|
Тоді cosϕ = ± 1− sin2 ϕ . Оскільки |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
5 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
; |
π |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ − |
2 |
, то в цьому проміжку |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos ϕ l 0, отже, cosϕ = 1− sin2 ϕ. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
148
§ 13. Обернені тригонометричні функції |
|
|
|||
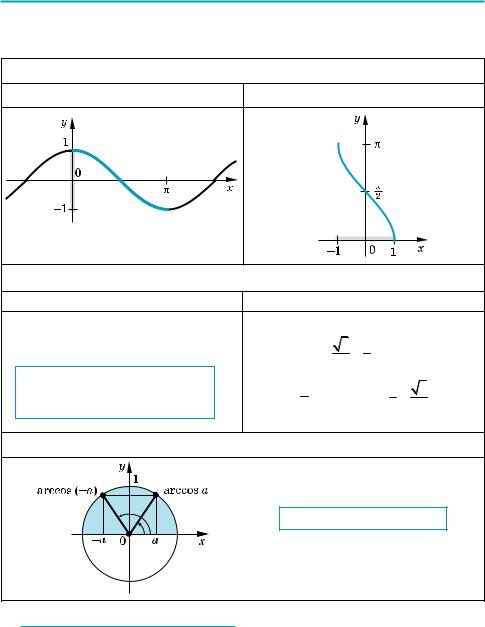
13.2. ФУНКЦІЯ y = arccos x |
|
|
|
|
|
|
|
|
|
Т а б л и ц я 27 |
|
1. Графік |
|
|
|
|
|
y = cos x |
|
y = arccos x |
|
||
На проміжку [0; π] cos x спадає. |
|
|
|
|
|
2. Значення arccos a (| a | m 1) |
|
|
|
||
Орієнтир |
|
|
Приклад |
|
|
arccos a — це таке число з проміжку |
|
|
|
|
|
[0; π], косинус якого дорівнює а. |
arccos |
2 = π , оскільки |
|||
|
|
|
2 |
4 |
|
ϕ [0; π], |
π |
|
|
π |
|
arccos a = ϕ, якщо |
[0; |
π] |
2 |
||
cosϕ = a |
4 |
і cos 4 = |
2 . |
||
3. Формула для arccos (–a) |
|
|
|
||
|
arccos (–a) = π – arccos a |
||||
Пояснення й обґрунтування |
|
|
|
|
|
1. Графік функції y = arccos x. Функція y = cos x спадає на проміжку [0; π] і набуває всіх значень від 1 до –1. Отже, на цьому проміжку функція y = cos x має обернену функцію, яка позначається y = arccos x, з областю визначення
149
РОЗДІЛ 2. Тригонометричні рівняння і нерівності
Рис. 88 |
Рис. 89 |
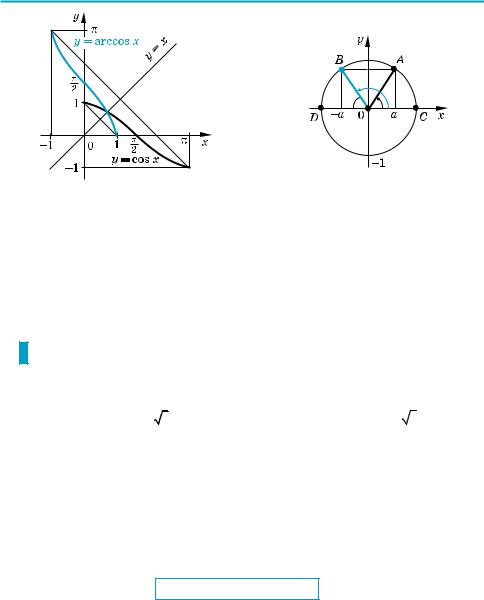
[–1; 1] і областю значень [0; π]. Функція y = arccos x теж спадає, і її графік можна одержати з графіка функції y = cos x (на заданому проміжку) за допо$ могою симетричного відображення його відносно прямої y = x (рис. 88).
2. Значення arccos a. За означенням оберненої функції (на вибраному про$ міжку), якщо cos ϕ = a, то arccos a = ϕ, причому ϕ [0; π] і | a | m 1. Отже, запис arccos a = ϕ (| a | m 1) означає, що ϕ [0; π] і cos ϕ = a, тобто
arccos a — це таке число з проміжку [0; π], косинус якого дорівнює a.
Наприклад, arccos |
1 |
= |
|
π |
, |
оскільки |
π |
[ |
] |
і |
cos |
π |
= |
1 |
. |
|
|
|
|
|||||
|
|
|
|
|
||||||||||||||||||||
2 |
3 |
3 |
0; π |
3 |
2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
3 |
|
|
|
5π |
|
|
|
5π |
[0; π] |
|
|
|
5π |
|
3 |
|
|||||
Аналогічно arccos − |
|
|
= |
, оскільки |
і cos |
= − |
. |
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
2 |
|
|
6 |
|
|
|
6 |
|
|
|
|
6 |
|
2 |
|
||||||
3. Формула для arccos (–a). Для знаходження арккосинусів від’ємних чисел можна також користуватися формулою arccos (–a) = π – arccos a.
(Це випливає з того, що точки a і (–a) на осі Оx (рис. 89) є симетричними
відносно осі Оy. Тоді і відповідні точки A і B на одиничному колі (у проміжку [0; π]) теж будуть симетричними відносно осі Оy. Отже, COA = DOB, значить, COB = π – DOB = π – COA. Але arccos a = COA, а arccos (–a) = COB = π – COA. Одержуємо
arccos (–a) = π – arccos a .
Наприклад, arccos (− |
1 |
)= π − arccos |
1 |
= π − π |
= |
2π |
. |
|
|
|
|||||
2 |
2 |
3 |
3 |
|
|||
Зазначимо, що рівність arccos (–a) = π – arccos a означає, що функція y = arccos x не є ні парною, ні непарною.
150
