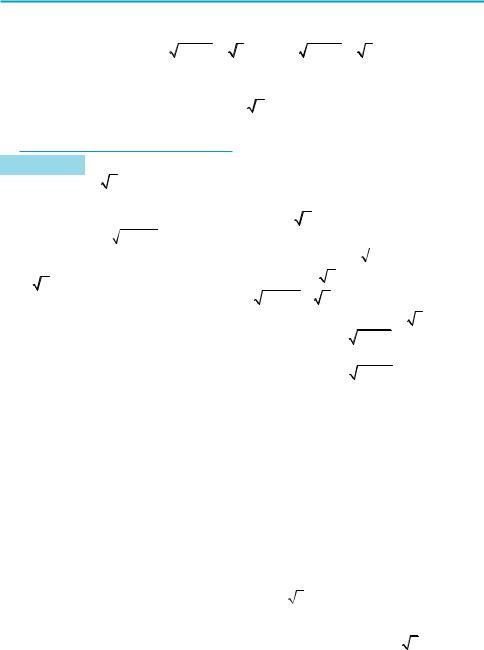Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Криворожский национальный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

algebra10_нелін_дворівн

.pdf

Скачиваний:

Добавлен:

22.03.2015

Размер:

5.24 Mб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 4514 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

§ 11. Додаткові формули тригонометрії


sin2 α =	1 − cosα		,	(3)
	2
2
cos2 α =		1+cosα		(4)

2	2

З формул (3) і (4) одержуємо формули половинного аргументу для синуса і косинуса:

sin	α	= ±	1 − cos α	,	(5)
sin	2	= ±	2	,	(5)
	2		2

cos	α =±		1+cos α	.	(6)
	2		2

У цих формулах знак перед коренем вибирається залежно від знаку триго$ нометричної функції, що стоїть у лівій частині рівності.

									sin α		= tg α ,
	Якщо почленно розділити формули (5) і (6) і врахувати, що									2
	Якщо почленно розділити формули (5) і (6) і врахувати, що									α
		α							cos	α	2
	cos								cos	2
			= ctg α , то одержуємо:
		2
а

		α
	sin	α	2
	sin	2
		2		tg	α =±	1 −cos α	,				(7)
				tg	α =±	1 −cos α	,				(7)
					2	1+cos α

				ctg α =±		1+cos α		.			(8)
					2	1 −cos α

У формулах (7) і (8) знак перед коренем також вибирається залежно від знаку тригонометричної функції, що стоїть у лівій частині рівності.

Зазначимо, що формули (5) і (6) можна використовувати при будь$яких

значеннях α, а формули (7) і (8) тільки тоді, коли існують значення tg α та

ctg α відповідно. Отже, формулу (7) можна використовувати, якщо α ≠ π + πk,

2 2 2

тобто α ≠ π + 2πk, k Z, а формулу (8) — якщо α ≠ πk, тобто α ≠ 2πk, k Z.

Зауважимо, що для тангенса і котангенса половинного аргументу можна одержати формули, які не містять квадратних коренів. Наприклад,

							tg α =	sin α	.	(9)
							tg α =	1 +cos α	.	(9)
							2	1 +cos α
Дійсно, якщо врахувати, що аргумент α вдвічі більший за аргумент										α , то
		α	α		α					2
		α	α		α
sinα	=	2sin 2 cos	2	=	sin 2	= tg α , якщо 1 + cos α ≠ 0, тобто формулу (9) можна
1 + cosα	=	2cos2 α		=	cos α	= tg α , якщо 1 + cos α ≠ 0, тобто формулу (9) можна
1 + cosα		2cos2 α			cos α	2
	2			2

використовувати при α ≠ π + 2πk, k Z.

131

РОЗДІЛ 1. Тригонометричні функції

Аналогічно обґрунтовується формула

α = 1 − cos α

(10)

2 sin α

1 − cos α

2sin

2 α

sin

= tg α , якщо sin α ≠ 0, тобто формулу (10) можна

sinα

2sin

cos

використовувати при α ≠ πk, k Z.

Враховуючи, що ctg

α =

, одержуємо формули:

tg α

ctg

α =

sin α

ctg

α = 1 + cos α

1 − cos α

sin α

4. Вираження тригонометричних функцій через тангенс половинного ар гументу. Щоб одержати відповідні формули для sin α і cos α запишемо кожен з цих виразів за формулами подвійного аргументу і поділимо на

1 = sin2 α + cos2 α . Потім, щоб перейти до тангенсів, поділимо чисельник і зна$

менник одержаного дробу на cos2 α (звичайно, за умови, що cos2 α ≠ 0, тобто

при α ≠ π + 2πk, k Z).														2																2
при α ≠ π + 2πk, k Z).
													2sin α cos α											sin α
															2			2		2						2
	sinα			2sin α cos α											cos2 α					2				cos		α				2tg α
				2sin α cos α											cos2 α									cos		α				2tg α
sinα =		=		2 2					=									2			=					2		=		2	. Отже,
sinα =		=		sin2 α + cos2 α					=			sin2 α + cos2 α									=		sin2 α					=			. Отже,
1				sin2 α + cos2 α								sin2 α + cos2 α											sin2 α							tg2 α + 1
			2				2								2			2					2			+ 1				2
			2				2								cos2 α								cos2 α			+ 1				2
															cos2 α								cos2 α
																		2		2

										2 tg				α
					sinα =									2		,		α ≠ π + 2πk, k Z											.	(11)
					sinα =											,		α ≠ π + 2πk, k Z											.	(11)
							1				+ tg			2	α
							1				+ tg			2	2
															2

						cos α				cos2 α − sin2 α											1 − tg2 α
			cosα =			cos α	=							2				2	=			2			.		Отже,
			cosα =				=												=						.
			1							sin2 α + cos2 α												tg2 α + 1
			1							sin2 α + cos2 α												tg2 α + 1
														2				2		2

								1			− tg2 α
					cosα =										2		,	α ≠ π + 2πk, k Z											.	(12)
					cosα =												,
								1			+ tg 2				α
								1			+ tg 2				2
															2

Якщо почленно поділити рівності (11) і (12), то одержимо формули:

132

§ 11. Додаткові формули тригонометрії

		2tg	α				π
tg α =		2tg	2	,	α ≠		π	+ πn, n Z, α ≠ π + 2πk, k Z					,	(13)
tg α =	1	− tg 2 α		,	α ≠		2	+ πn, n Z, α ≠ π + 2πk, k Z					,	(13)
			2

						1	− tg2 α
			ctg α =						2	,	α ≠ πk, k Z	.
			ctg α =				2 tg		α	,	α ≠ πk, k Z	.
									α
									2
									2

Зауважимо, що формулу (13) можна одержати і за формулою тангенса по$

двійного аргументу, оскільки α = 2 α .

Приклади розв’язання завдань

Приклад 1 Обчисліть, не користуючись таблицями і калькулятором:

1) sin 15°;

2) cos 15°;

3) tg 15°.

Р о з в ’ я з а н н я

К о м е н т а р

1) X sin 15° =

1 − cos 30°

Оскільки аргумент 15° становить

половину від аргументу 30°, а коси$

нус 30° нам відомий, то можна знай$

ти шукані значення за формулами по$

1 −

2 −

ловинного аргументу. Враховуючи,

; Y

що аргумент 15° знаходиться в I чвер$

ті (де значення всіх тригонометрич$

2) X cos 15° =

1 + cos30°

них функцій додатні), у формулах (5)

і (6) перед знаком квадратного коре$

ня вибирається знак «+». Для зна$

1 +

2 +

ходження тангенса 15° можна вико$

; Y

ристати будь$яку з формул (7), (9) або

(10), але зручніше використати фор$

мули (9) або (10), запис яких не міс$

3)X tg15° = 1 − cos30°

1 −

тить квадратних коренів. Також піс$

= 2 −

3.Y

ля знаходження sin 15° і cos 15° мож$

sin30°

на використати формулу

tg15° =

sin15°

cos15°

З а у в а ж е н н я. Записи відповідей для sin 15° і cos 15° можна дещо спрос$ тити, виділяючи під знаком зовнішнього квадратного кореня квадрат дво$ члена. Щоб подати, наприклад, 2 − 3 у вигляді квадрата двочлена, помно$ жимо і поділимо цей вираз на 2 (та розглянемо вираз 2 3 як подвоєний добу$ ток чисел 3 і 1). Одержуємо:

133

РОЗДІЛ 1. Тригонометричні функції

							2 +		3 =	4 + 2 3		=	(	3 + 1)2
													(	3 + 1)2
														.
										2				.
										2				2
(			3 − 1)2
Тоді sin15° =	2 − 3	=	2		=	3 − 1		=	6 − 2		.
Тоді sin15° =		=	2		=			=	4		.
2			2	2			2		4
				2			2
Виконуючи аналогічні перетворення, маємо cos 15° =														6 + 2	.
Виконуючи аналогічні перетворення, маємо cos 15° =														4	.
														4

Запитання для контролю

1.Запишіть формули потрійного та половинного аргументів і формули вира$ ження тригонометричних функцій через тангенс половинного аргументу. Проілюструйте на прикладах застосування цих формул.

2.Обґрунтуйте формули потрійного та половинного аргументів і формули вираження тригонометричних функцій через тангенс половинного аргу$ менту.

	Вправи
1.	Обчисліть, не користуючись таблицями і калькулятором:
	1) sin 22°30R;								2) cos 22°30R;																		3) tg 22°30R.
2.	Знайдіть sin α ; cos α ; tg α ,										якщо:
			2			2			2
	1) cosα = −	3	і π < α <				3π	;			2) cosα =							5		і		3π		< α < 2π.
	1) cosα = −		і π < α <					;			2) cosα =									і				< α < 2π.
	5					2					13									2
3.	Обчисліть tg(α+			π	), якщо cos2α =											1			і π < α <							5π	.
3.	Обчисліть tg(α+			π	), якщо cos2α =														і π < α <								.
			4								3									4
4.	Обчисліть cos α , якщо sinα = −													12	і π < α <								3π		.
4.	Обчисліть cos α , якщо sinα = −														і π < α <										.
			2								13									2
5.	Обчисліть sinα, якщо tg α =											1	.
5.	Обчисліть sinα, якщо tg α =												.
									2		3
6.	Обчисліть tg α , якщо sinα + cosα =																1		і	3π	< α < 2π.
6.	Обчисліть tg α , якщо sinα + cosα =																		і	2	< α < 2π.
			2								5									2
7.	Обчисліть		sin2α			cos α				, якщо tg α = 2.
	1		+ cos α			1 + cos2α					2
8.	Враховуючи, що sin 36° = cos 54°, обчисліть sin 18°.

134

§11. Додаткові формули тригонометрії

11.2.ФОРМУЛА ПЕРЕТВОРЕННЯ ВИРАЗУ a sin α + b cos α

Т а б л и ц я 24

asinα+ bcosα= a2 + b2 sin(α+ ϕ) ,

де аргумент ϕ визначається із співвідношень

cosϕ =	a	, sinϕ =	b
	a2 + b2		a2 + b2

Пояснення й обґрунтування

(Спочатку доведемо таке твердження: якщо для чисел m і n виконується

співвідношення m2 + n2 = 1, то одне з цих чисел можна вважати синусом, а друге косинусом деякого аргументу ϕ.

Розглянемо точку M координатної площини з координатами M (m; n). Координати точки М задовольняють рівнянню одиничного кола: x2 + y2 = 1 (оскільки за умовою т2 + п2 = 1). Oтже, точка M знаходиться на одинично$ му колі, і її абсциса є косинусом кута ϕ, який утворює радіус OM з додат$ ним напрямком осі Ox, а ордината — синусом цього кута ϕ. Тобто m = cos ϕ, n = sin ϕ.

Якщо взяти m =

n =

то

m2 + n2

= 1. Тоді

+ b2

a2 + b2

для деякого кута ϕ

m =

= cos ϕ,

n =

= sin ϕ.

a2 + b2

Тепер ми можемо довести формулу a sinα + b cosα = a2 + b2 sin(α + ϕ). Для цього доведемо, що права частина цієї формули дорівнює лівій.

a2 + b2 sin(α + ϕ) =			a2 + b2 (sinα cosϕ + cosα sinϕ) =
= a2 + b2 sinα	a		+ cosα			b		= a sinα + b cosα,

	a2 + b2					a2 + b2
що й потрібно було довести. Отже,
asinα+ bcosα=					a2 + b2 sin(α+ ϕ),
де аргумент ϕ визначається із співвідношень:
cos ϕ =			a	, sin ϕ =				b	.)
		a2 + b2					a2 + b2

З а у в а ж е н н я. В одержаній формулі аргумент ϕ визначається з точні$ стю до 2π, але найчастіше вибирають те значення, яке найменше за моду$ лем.

135

РОЗДІЛ 1. Тригонометричні функції

Наприклад, для виразу sin α + cos α маємо a = 1, b = 1. Тоді

cosϕ =

sinϕ =

a2 + b2

Отже, аргумент ϕ знаходиться в I чверті і як значення ϕ можна вибрати

ϕ =

. Тоді

sinα + cosα =

2 sin(α +

)

Приклади розв’язання завдань

Приклад 1 Знайдіть найбільше та найменше значення виразу 3sinα − cosα.

Р о з в ’ я з а н н я

К о м е н т а р

X За формулою

Вираз

3sinα − cosα можна перетво$

asinα + bcosα = a2 + b2 sin(α + ϕ)

рити за формулою

a2 + b2 sin(α + ϕ).

одержуємо

asinα + bcosα =

3sinα − cosα = 2sin(α − π ).

Тут a =

3, b = –1, тоді

a2 + b2 =

4 = 2. Отже,

Враховуючи, що sin(α − 6π ) набу$

cosϕ =

a2 + b2

ває всіх значень із проміжку [–1; 1],

sinϕ =

= −

a2 + b2

маємо, що 2 sin(α − 6 ) набуває всіх

Тоді аргумент ϕ знаходиться в

значень із проміжку [–2; 2]. Отже,

IV чверті, і як значення ϕ можна ви$

найбільше значення заданого виразу

брати, наприклад, ϕ = −

. Викорис%

дорівнює 2, а найменше — (–2). Y

товуючи метод оцінки для знахо%

дження найбільшого та найменшого

значень виразу, враховуємо, що необ%

хідно не тільки оцінити значення ви%

разу за допомогою нестрогих нерівно%

стей

(−2 m 2sin(α − π )

m 2), а й впев%

нитися, що знак рівності в цих не%

рівностях досягається.

Побудуйте графік функції y =

2 (sinx + cosx).

Приклад 2

К о м е н т а р

2sin(x +

Вираз sin x + cos x можна записати у вигляді sin x + cos x =

Тоді графік заданої функції можна побудувати за допомогою геометричних перетворень графіка функції y = sin x.

136

§ 11. Додаткові формули тригонометрії

Р о з в ’ я з а н н я

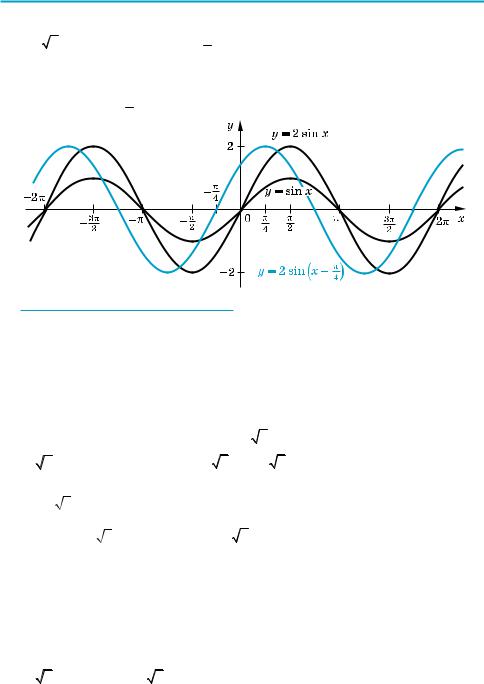
X y = 2(sinx + cosx) = 2 sin(x + π4 ).

Графік заданої функції одержуємо з графіка функції y = sin x розтягуван$ ням у 2 рази вздовж осі Оy і паралельним перенесенням отриманого графіка

вздовж осі Оx на (− π4 ).

Запитання для контролю

1.Запишіть формулу перетворення виразу a sin α + b cos α на вираз вигляду c sin (x + ϕ). Проілюструйте на прикладі застосування цієї формули.

2.Обґрунтуйте формулу перетворення виразу a sin α + b cos α на вираз вигля$ ду c sin (x + ϕ).

	Вправи
1.	Знайдіть найбільше та найменше значення виразу:
	1) sin α + cos α;	2)	sinα − 3cosα;
	3) 3sinα + cosα;	4)	2sinα +		6 cosα.
2.	Побудуйте графік функції:
	1) y = 3 sin x + cos x;	2)	y = sin 2x − cos 2x;
	3) y = sin x + 3 cos x;	4)	y = 3sin	x	+ cos	x	.
	3) y = sin x + 3 cos x;	4)	y = 3sin		+ cos		.
			2		2

3.Знайдіть область значень функції:

1) y = 3 sin x + 4 cos x; 2) y = 5 sin 3x – 12 cos 3x;

3) y = sin 7x – cos 7x;	4)	y = 8sin	x	+ 15cos	x	.

		3		3

4.Чи існують такі значення x, при яких виконується рівність: 1) 3 sin x – 4 cos x = 6; 2) 5 sin 2x + 12 cos 2x = 15;

3) 3sin4x − cos4x = 5;	4) sin	x	+ cos	x	= 1,5?

137

ДОДАТКОВІ ВПРАВИ ДО РОЗДІЛУ 1

Спростіть вираз (1–2).

1) tg2 α – sin2 α – tg2 α sin2 α;

sin2 β(1 + ctgβ) + cos2 β(1 + tgβ);

3) (3 sin α + 2 cos α)2 + (2 sin α – 3 cos α)2;

cos β tg

− ctg βcos β.

sin2 β

1) 2 tg α − tg(α − π) + ctg(

3π

− α );

sin(−α )

−

tg(2π − α )

cos α

;

sin(π − α )

(

+ α )

ctgα

sin

tg(π − β )cos(π − β )tg(

− β )

sin(

− β )ctg(

+ α )tg(3π + α )

Доведіть тотожність (3–4).

3. 1)

tg(α + β ) − tg α − tg β

= tg β;

tg α tg(α + β )

cos(α + β ) + cos(α − β )

= ctg α;

sin(α + β ) + sin(α − β )

	tg(3π + α )sin 3π sin 16π cos 13π
4)	2	2	9	18	.
4)					.
	ctg(π − α )cos 5π sin 11π cos2π
		18	9
2)	1 − cos2α + sin2α		= tg α;
2)	1 + cos2α + sin2α		= tg α;
	1 + cos2α + sin2α
4)	sinα − sin3α	= − ctg 2α.
4)	cos α − cos 3α	= − ctg 2α.
	cos α − cos 3α

4.	1)			1		−	1				1		+				1		cosα = cos α						при π < α < 2π;
4.	1)	2				−	2			2			+				2		cosα = cos α						при π < α < 2π;
		2					2			2							2					4
	2)		1−					1		−				1		cos 2α = 2cos(											π	− α )		при π < α <					3π	;
								1						1													π
								2						2
								2						2											4				2			2
	3)	1				+	1			1				+			1		cos 2α = − cos						α				при		3π	< α < 2π;
																															2
					2		2			2								2							2						2
								1						1										π					α				3π
	4)	1+								−						cosα =						2cos(				−			4 )	при				< α < 2π.
																																	2
								2							2									4									2
5.	Доведіть рівність:
	1)	cos π cos										4π				cos				5π	=	1	;		2) tg 20° – 4 sin 20° sin 50° = –2 sin 20°;
	1)	cos π cos														cos					=	8	;		2) tg 20° – 4 sin 20° sin 50° = –2 sin 20°;
		7								7							7					8
	3)	1							− 4 sin 70° = 2;																4) cos 20° + 2 sin 55° − 2 sin 65° = 1.
	3)		sin 10°						− 4 sin 70° = 2;																4) cos 20° + 2 sin 55° − 2 sin 65° = 1.
																														138

Відомості з історії

6. Доведіть, що правильна нерівність:						sin(		+ α )
	π						π				α
1) tg x + ctg x l 2, якщо 0 < x <		;	2)				3			+ 2 sin		m2 3;
							3
	2			sin(	π	+ α )sin(5π − α )					2
	2			sin(		+ α )sin(5π − α )
				12		4	12		4

3)(1 + sin ϕ + cos ϕ)(1 – sin ϕ + cos ϕ)(1 + sin ϕ – cos ϕ)(sin ϕ + cos ϕ – 1) m 1;

4)2 sin 4α sin 2α + cos 6α l –1.

7.Обчисліть:

		α + sin		α, якщо sin2α =				2			1 − sin2		α			tg α = m;
1) cos	4		4					2	;	2)	1 − sin2		2	, якщо		tg α = m;
1) cos							3		;	2)	1 + sinα			, якщо		2
3) cos α, якщо sin α tg α =					1	;
3) cos α, якщо sin α tg α =						;
				2
4) sin α, cos 2α, cos α , якщо tg α = −										2, π < α <		3π			.
4) sin α, cos 2α, cos α , якщо tg α = −										2, π < α <					.
				2			2				2

ВІДОМОСТІ З ІСТОРІЇ

Слово «тригонометрія» вперше зустрічається (1505 р.) у назві книжки німецького теолога і математика П и т и с к у с а. Походження цього слова грецьке: «тригонон» — трикутник, «метріо» — міра. Іншими словами, три$ гонометрія — наука про вимірювання трикутників. Багато понять і фактів, які тепер відносять до тригонометрії, були відомі ще дві тисячі років тому. Фактично різні відношення відрізків трикутника і кола (власне кажучи, і три$ гонометричні функції) зустрічаються вже в III ст. до н. е. в працях великих математиків Стародавньої Греції — Е в к л і д а та А р х і м е д а.

Довгий час тригонометрія розвивалася як частина геометрії, тобто факти, які ми тепер формулюємо в термінах тригонометричних функцій, формулю$ вали і доводили за допомогою геометричних понять і тверджень. Мабуть, найбільші стимули для розвитку тригонометрії виникали у зв’язку з розв’я$ зуванням задач астрономії, що становило великий практичний інтерес (на$ приклад, для розв’язування задач на визначення місцезнаходження судна, передбачення затемнень тощо). Сучасного вигляду тригонометрії надав вели$ кий математик XVIII ст. Л. Е й л е р (1707—1783), швейцарець за похо$ дженням, який довго працював у Росії і був членом Петербурзької академії наук. Саме Ейлер перший увів відомі означення тригонометричних функцій, почав розглядати функції довільного кута, вивів формули зведення. Після Ейлера тригонометрія набрала форми числення: різні факти почали доводити формальним застосуванням формул тригонометрії, доведення стали набага$ то компактнішими.

139

Розділ 2

Тригонометричні рівняння і нерівності

§12 ОБЕРНЕНА ФУНКЦІЯ

Т а б л и ц я 25

1. Поняття оберненої функції

Якщо функція y = f (x) набуває кожного свого значення в єдиній точці її області визначення, то можна задати функцію y = g (x), яка називаєть ся оберненою до функції y = f (x):

для кожного a D (f) , якщо f (a) = b, то g (b) = a

E (f) =D (g); D (f) = E (g)

Функції f (x) і g (x) взаємно обернені.

2. Властивості оберненої функції

1) Графіки прямої і оберненої

функцій симетричні відносно прямої y = x.

2) Якщо функція f (x) зростає (спа

дає) на деякому проміжку, то вона має обернену функцію на цьому проміжку, яка зростає, якщо f (x) зростає, і спадає, якщо f (x) спадає.

140

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 4514 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.03.20158.49 Mб8978-966-00-1063-5.pdf
#
07.03.2016315.39 Кб16ADMINISTRATIVNO_PRAVOVIJ_STATUS_MON-2.doc
#
07.03.2016359.42 Кб11AGRARNA_POLITIKA_UTsR_DIPLOMNA_ROBOTA.doc
#
21.11.2019178.18 Кб5Alekhina_glava4-97.doc
#
09.11.20194.5 Mб21Alesinskaya_Reshenie_zadach_Ekonom_metody_model...doc
#
22.03.20155.24 Mб60algebra10_нелін_дворівн.pdf
#
07.03.20161.34 Mб214AMMA.doc
#
12.11.20181.63 Mб22Angl.doc
#
30.04.201517.56 Кб45angl.docx
#
22.03.201533.28 Кб278Annotatsia_proizvedenia_Groza.doc
#
22.03.201545.11 Mб46Antichnaya_mifologia_Entsiklopedia.rtf