
algebra10_нелін_дворівн
.pdf
§ 5. Графіки функцій синуса, косинуса, тангенса і котангенса та їх властивості
Пояснення й обґрунтування
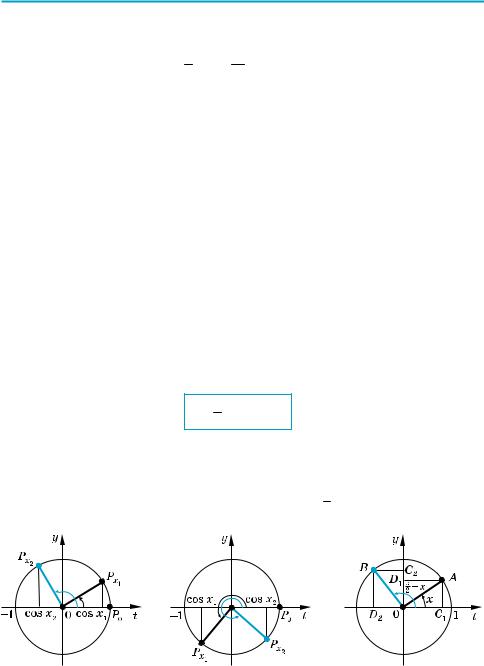
Нагадаємо, що значення косинуса — це абсциса відповідної точки одинич ного кола (рис. 57). Оскільки абсцису можна знайти для будь якої точки оди ничного кола, то область визначення функції y = cos x — усі дійсні числа. Це можна записати так:
D (cos x) = R.
Для точок одиничного кола абсциси набувають усіх значень від –1 до 1, отже, область значень функції y = cos x: y [–1; 1]. Це можна записати так:
E (cos x) = [–1; 1].
Як бачимо, найбільше значення функції cos x дорівнює одиниці. Це зна чення досягається тільки тоді, коли відповідною точкою одиничного кола є точка A, тобто при x = 2πk, k Z.
Найменше значення функції cos x дорівнює мінус одиниці. Це значення досягається тільки тоді, коли відповідною точкою одиничного кола є точ ка B, тобто при x = π + 2πk, k Z.
Як було показано в § 4, косинус — парна функція: cos (– x) = cos x, тому її графік симетричний відносно осі Оу.
У § 4 було обґрунтовано також, що косинус — періодична функція з най меншим додатним періодом T = 2π: cos (x + 2π) = cos x. Отже, через проміжки довжиною 2π вид графіка функції cos x повторюється.
Щоб знайти точки перетину графіка функції з осями координат, згадає мо, що на осі Oy значення x = 0. Тоді відповідне значення y = cos 0 = 1.
На осі Ox значення y = 0. Отже, нам потрібні такі значення x, при яких cos x, тобто абсциса відповідної точки одиничного кола, буде дорівнювати нулю. Це буде тільки тоді, коли відповідною точкою одиничного кола є точка C
або D, тобто при x = π + πk, k Z. |
|
|
|
|||
|
|
2 |
|
|
|
|
Проміжки знакосталості. Як було обґрунтовано в § 4, значення функції |
||||||
косинус додатні (тобто абсциса відповідної точки одиничного кола додатна) |
||||||
в I і IV чвертях (рис. 58). Отже, cos x > 0 при x (− |
2π; |
2π ), а також, враховуючи |
||||
період, при всіх x |
( |
− π + 2πk; π + 2πk , k Z. |
|
|
||
|
2 |
2 |
) |
|
|
|
Рис. 57 |
|
|
|
Рис. 58 |
||
|
|
|
|
61 |
|
|
РОЗДІЛ 1. Тригонометричні функції
Значення функції косинус від’ємні (тобто абсциса відповідної точки одиничного кола від’ємна) у ІІ і ІІІ чвертях, отже, cos x < 0 при
x (2π + 2πk; 32π + 2πk), k Z.
Проміжки зростання і спадання.
(Враховуючи періодичність функції cos x (T = 2π), досить дослідити її на зростання і спадання на будь якому проміжку довжиною 2π, наприклад, на проміжку [0; 2π].
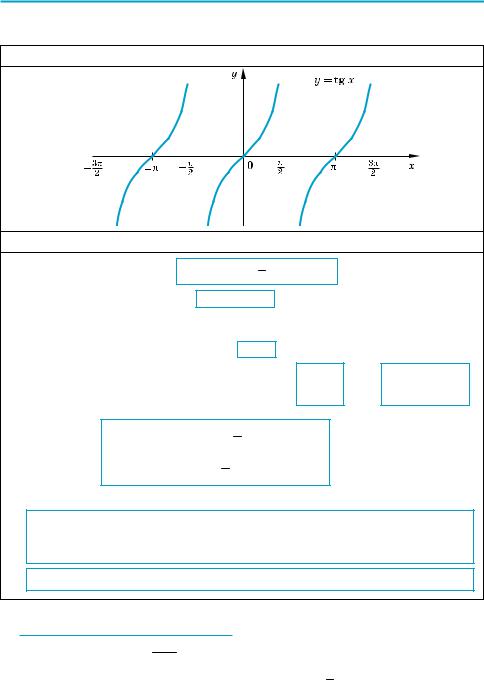
Якщо x [0; π] (рис. 59, а), то при збільшенні аргументу x (x2 > x1) абсциса відповідної точки одиничного кола зменшується (тобто cos x2 < cos x1), отже, у цьому проміжку функція cos x спадає. Враховуючи періодичність
функції cos x, робимо висновок, що вона також спадає в кожному з про міжків [2πk; π + 2πk], k Z.
Якщо x [π; 2π] (рис. 59, б), то при збільшенні аргументу x (x2 > x1) абсци са відповідної точки одиничного кола збільшується (тобто cos x2 > cos x1), отже, у цьому проміжку функція cos x зростає. Враховуючи періодичність
функції cos x, робимо висновок, що вона також зростає в кожному з про міжків [π + 2πk; 2π + 2πk], k Z. )
Проведене дослідження дозволяє побудувати графік функції y = cos x ана логічно до того, як було побудовано графік функції y = sin x. Але графік функції у = cos x можна також одержати за допомогою геометричних перетворень гра фіка функції у = sin х, використовуючи формулу
sin(2π + x)= cosx .
( Цю формулу можна обґрунтувати, наприклад, так. Розглянемо одиничне
коло (рис. 60) і відмітимо на ньому точки А = Рх і B = Pπ2 +x та абсциси
і ординати цих точок. Враховуючи, що AOB = π , одержуємо, що при по
2
а |
б |
Рис. 59 |
Рис. 60 |
62

§ 5. Графіки функцій синуса, косинуса, тангенса і котангенса та їх властивості
Рис. 61
вороті прямокутника OC |
AD |
|
|
|
навколо точки О на кут |
π |
проти годиннико |
|||||||||||||||||
1 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
вої стрілки, він перейде в прямокутник OC2ВD2. Але тоді ОD2 = ОD1 |
||||||||||||||||||||||||
і ОС = ОС . Отже, sin( |
π |
+ x) |
|
|
= y |
|
= OC = OC = t |
|
= cosx. |
|||||||||||||||
|
B |
A |
||||||||||||||||||||||
2 |
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Зазначимо також формули, які нам знадобляться далі: |
||||||||||||||||||||||||
|
|
cos( |
π |
+ x)= tB = − OD2 = − OD1 = −yA = − sinx. Тоді, |
||||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
sin( |
|
|
|
|
+ x) |
|
|
|
|
|
|
|||||
|
|
tg( |
π |
+ x)= |
|
π |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
cos x |
|
|
|
|
|
|||||||||||||||
|
|
|
2 |
|
|
|
|
= |
= − ctgx. Отже, |
|||||||||||||||
|
|
2 |
cos( |
π |
+ x) |
− sin x |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
tg(2π + x)= − ctgx . )
Враховуючи, що cosx = sin(x + 2π ), графік функції y = cos x можна одер жати із графіка функції y = sin x його паралельним перенесенням уздовж осі Ох на (− 2π ) (рис. 61). Одержуємо графік, який називається косинусоїдою
(рис. 62).
Рис. 62
63
|
РОЗДІЛ 1. Тригонометричні функції |
|
|||
5.3. ГРАФІК ФУНКЦІЇ y = tg x ТА ЇЇ ВЛАСТИВОСТІ |
|
|
|||
|
|
|
|
|
Т а б л и ц я 12 |
|
Графік функції y = tg x (тангенсоїда) |
|
|||
|
Властивості функції y = tg x |
|
|
||
1. |
Область визначення: D (tg x): x ≠ π + πk, k Z . |
|
|||
|
|
2 |
|
|
|
2. |
Область значень: y R. |
E (tg x) = R |
|
|
|
3. |
Функція непарна: tg (–x) = –tg x |
|
|
|
|
|
(графік симетричний відносно початку координат). |
|
|||
4. |
Функція періодична з періодом T = π : |
tg (x + π) = tg x. |
|||
|
|
|
x = 0, |
y = 0, |
|
5. |
Точки перетину з осями координат: Оy y = 0 |
Оx |
x = πk, k Z |
||
6. |
Проміжки знакосталості: |
|
|
|
|
|
tg x > 0 при x (πk; 2π + πk), |
k Z |
|
|
|
|
tg x < 0 при x (− π + πk; πk), k Z |
|
|
||
|
|
2 |
|
|
|
7. Проміжки зростання і спадання: |
|
|
|
||
|
функція tg x зростає на кожному з проміжків своєї області визначення, |
||||
|
тобто на кожному з проміжків (− π + πk; |
π + πk), |
k Z. |
|
|
|
|
2 |
2 |
|
|
8. |
Найбільшого і найменшого значень функція не має. |
|
|||
Пояснення й обґрунтування |
|
|
|
||
Нагадаємо, що tgx = sinx . Отже, областю визначення тангенса будуть всі
cos x
значення аргументу, при яких cos х ≠ 0, тобто x ≠ π + πk, k Z. Одержуємо
2
64
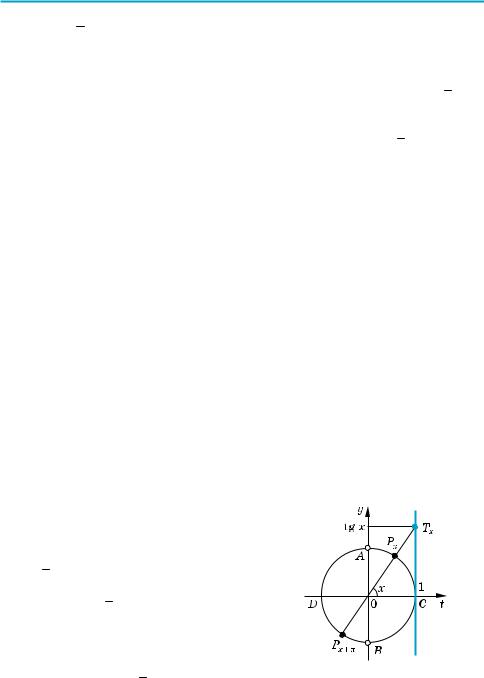
§ 5. Графіки функцій синуса, косинуса, тангенса і котангенса та їх властивості
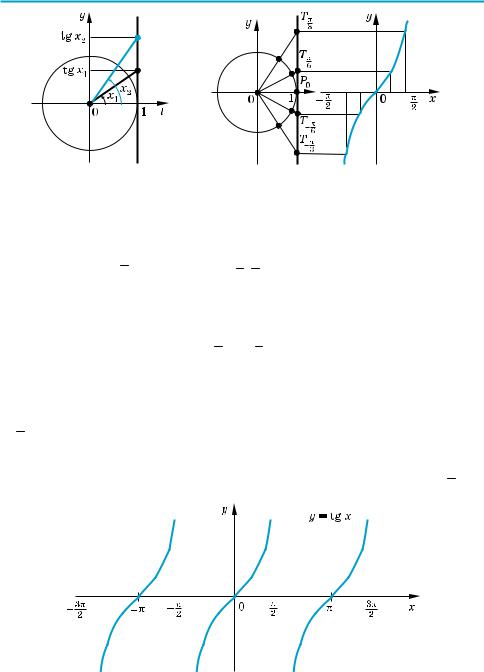
D (tg x): x ≠ 2π + πk, k Z. Цей результат можна одержати і геометрично. Зна
чення тангенса — це ордината відповідної точки Тх на лінії тангенсів (рис. 63). Оскільки точки А і В одиничного кола лежать на прямих ОА і ОВ, паралель
них лінії тангенсів, ми не зможемо знайти значення тангенса для x = π + πk,
2
k Z. Для всіх інших значень аргументу ми можемо знайти відповідну точку
на лінії тангенсів і її ординату — тангенс. Отже, всі значення x ≠ π + πk входять
2
до області визначення функції у = tg х.
Для точок одиничного кола (які не збігаються з точками А і В) ординати відповідних точок на лінії тангенсів набувають усіх значень від – до + . Таким чином, область значень функції y = tg x — всі дійсні числа, тобто y R. Це можна записати так: E (tg x) = R. З наведених міркувань також випливає, що найбільшого і найменшого значень функція tg x не має.
Як було показано в § 4, тангенс — непарна функція: tg (–x) = –tg x, отже, її графік симетричний відносно початку координат.
Тангенс — періодична функція з найменшим додатним періодом T = π: tg (x + π) = tg x (див. § 4). Тому при побудові графіка цієї функції досить побу дувати графік на будь якому проміжку довжиною π, а потім одержану лінію перенести паралельно праворуч і ліворуч уздовж осі Ox на відстані kT = πk, де k — будь яке натуральне число.
Щоб знайти точки перетину графіка функції з осями координат, згадає мо, що на осі Oy значення x = 0. Тоді відповідне значення y = tg 0 = 0, тобто графік функції y = tg x проходить через початок координат.
На осі Ox значення y = 0. Отже, нам потрібні такі значення x, при яких tg x, тобто ордината відповідної точки лінії тангенсів, дорівнюватиме нулю. Це буде тільки тоді, коли відповідною точкою одиничного кола є точка C
або D (рис. 63), тобто при x = πk, k Z. |
|
|||
Проміжки знакосталості. Як було |
|
|||
обґрунтовано в § 4, значення функції |
|
|||
тангенс додатні (тобто ордината відпо |
|
|||
відної точки лінії тангенсів додатна) |
|
|||
у I і III чвертях. Отже, tg x > 0 при |
|
|||
x (0; 2π ), а також, враховуючи період, |
|
|||
при всіх x (πk; 2π + πk), k Z. |
|
|
||
Значення функції тангенс від’ємні |
|
|||
(тобто ордината відповідної точки лінії |
|
|||
тангенсів від’ємна) у ІІ і ІV чвертях. От |
|
|||
же, tg x < 0 при x |
( |
− π + πk; πk , k Z. |
Рис. 63 |
|
|
2 |
) |
||
65
РОЗДІЛ 1. Тригонометричні функції
Рис. 64 |
Рис. 65 |
Проміжки зростання і спадання.
(Враховуючи періодичність функції tg x (період T = π), досить дослідити її
на зростання і спадання на будь якому проміжку довжиною π, наприклад, на проміжку (− 2π; 2π ). Якщо x (− 2π; 2π)(рис. 64), то при збільшенні аргу
менту x (x2 > x1) ордината відповідної точки лінії тангенсів збільшується (тобто tg x2 > tgx1). Отже, у цьому проміжку функція tg x зростає. Врахо
вуючи періодичність функції tg x, робимо висновок, що вона зростає та кож у кожному з проміжків (− 2π + πk; 2π + πk), k Z. )
Проведене дослідження дозволяє обґрунтовано побудувати графік функції y = tg x. Враховуючи періодичність цієї функції (з періодом π), спочатку побу дуємо графік на будь якому проміжку довжиною π, наприклад, на проміжку
(− 2π; 2π ). Для більш точної побудови точок графіка скористаємося також тим, що значення тангенса — це ордината відповідної точки лінії тангенсів. На рисунку 65 показана побудова графіка функції y = tg x на проміжку (− 2π; 2π ).
Рис. 66
66
§ 5. Графіки функцій синуса, косинуса, тангенса і котангенса та їх властивості
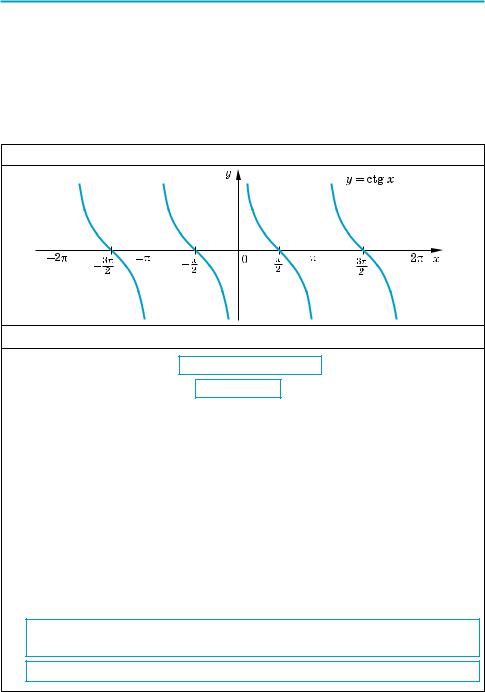
Далі, враховуючи періодичність тангенса (з періодом π), повторюємо ви гляд графіка на кожному проміжку довжиною π (тобто паралельно переноси мо графік уздовж осі Ох на πk, де k — ціле число).
Одержуємо графік, наведений на рисунку 66, який називається танген( соїдою.
5.4. ГРАФІК ФУНКЦІЇ y = ctg x ТА ЇЇ ВЛАСТИВОСТІ
Т а б л и ц я 13
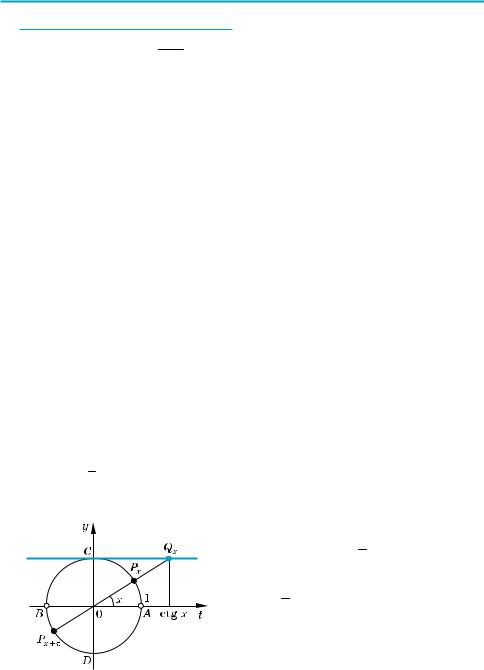
Графік функції y = ctg x (котангенсоїда)
Властивості функції y = ctg x
1.Область визначення: D (ctg x): x ≠ πk, k Z
2.Область значень: y R. E (ctg x) = R
3.Функція непарна: ctg (–x) = –ctg x
(графік симетричний відносно початку координат).
4. |
Функція періодична з періодом |
T = π |
: |
ctg (x + π) = ctg x. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
0, |
||
|
Точки перетину з осями координат: Оy |
|
|
Оx |
|
|
|
|
||||||||
5. |
немає |
|
|
|
π |
+ πk, k Z |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6. |
Проміжки знакосталості: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
2 |
) |
|
|
|
|
|
|
|
|
|
|
|
ctg x > 0 при x |
|
πk; |
π |
+ πk , k Z |
|
|
|
|
|
|
||||
|
( |
|
|
|
|
|
|
|
||||||||
|
|
|
2 |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
ctg x < 0 при x |
|
π |
+ πk; π + πk , k Z |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||
7.Проміжки зростання і спадання:
функція ctg x спадає на кожному з проміжків своєї області визначен! ня, тобто на кожному з проміжків (πk; π + πk), k Z.
8.Найбільшого і найменшого значень функція не має.
67
РОЗДІЛ 1. Тригонометричні функції
Пояснення й обґрунтування
Нагадаємо, що ctgx = cos x . Отже, областю визначення котангенса будуть
sinx
всі значення аргументу, при яких sin х ≠ 0, тобто x ≠ πk, k Z. Таким чином,
D (ctg x): x ≠ πk, k Z.
Той самий результат можна одержати, використовуючи геометричну ілюст рацію. Значення котангенса — це абсциса відповідної точки на лінії котан генсів (рис. 67). Оскільки точки А і В одиничного кола лежать на прямих ОА і ОВ, паралельних лінії котангенсів, ми не зможемо знайти значення котан генса для x = πk, k Z. Для всіх інших значень аргументу ми можемо знайти відповідну точку на лінії котангенсів і її абсцису — котангенс. Таким чином, усі значення x ≠ πk входять до області визначення функції у = ctg х.
Для точок одиничного кола (які не збігаються з точками А і В) абсциси відповідних точок на лінії котангенсів набувають усіх значень від – до + , отже, область значень функції y = ctg x — усі дійсні числа, тобто y R. Це можна записати так: E (ctg x) = R. З наведених міркувань також випливає, що найбільшого і найменшого значень функція ctg x не має.
Як було показано в § 4, котангенс — непарна функція: ctg (–x) = –ctg x, тому її графік симетричний відносно початку координат.
Також в § 4 було обґрунтовано, що котангенс — періодична функція з най меншим додатним періодом T = π: ctg (x + π) = ctg x, тому через проміжки довжиною π вигляд графіка функції ctg x повторюється.
Щоб знайти точки перетину графіка функції з осями координат, згадає мо, що на осі Oy значення x = 0. Але ctg 0 не існує, значить, графік функції y = ctg x не перетинає вісь Oy.
На осі Оx значення y = 0. Отже, нам потрібні такі значення x, при яких ctg x, тобто абсциса відповідної точки лінії котангенсів, дорівнюватиме нулю. Це буде тільки тоді, коли відповідною точкою одиничного кола є точка C або D,
тобто при x = π + πk, k Z. |
|
2 |
|
Проміжки знакосталості. Як було обґрунтовано в § 4, значення функції |
|
котангенс додатні (тобто абсциса відповідної точки лінії котангенсів додат |
|
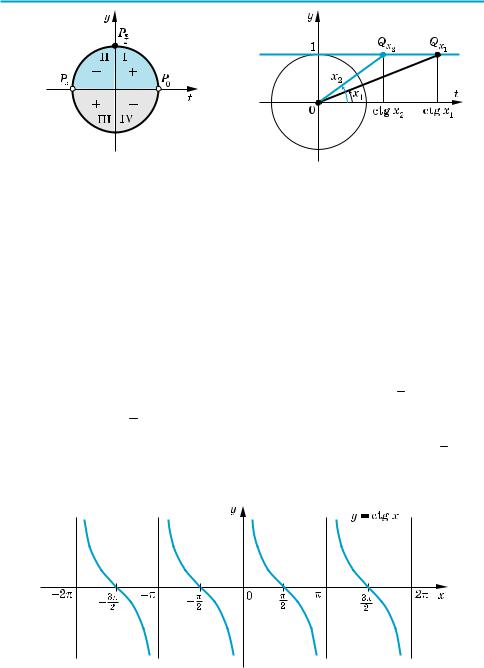
на) у I і III чвертях (рис. 68). Тоді |
|
ctg x > 0 при x |
0; π . Враховуючи пе |
( |
2 ) |
ріод, отримуємо, що ctg x > 0 при всіх x (πk; 2π + πk), k Z.
|
Значення функції котангенс від’ємні |
||
|
(тобто абсциса відповідної точки лінії |
||
|
котангенсів від’ємна) у ІІ і ІV чвертях, от |
||
|
же, ctg x < 0 при x ( |
π |
+ πk; π + πk), k Z. |
Рис. 67 |
2 |
||
68
§ 5. Графіки функцій синуса, косинуса, тангенса і котангенса та їх властивості
Рис. 68 |
Рис. 69 |
Проміжки зростання і спадання.
(Враховуючи періодичність функції ctg x (найменший додатний період T = π),
досить дослідити її на зростання і спадання на будь якому проміжку дов жиною π, наприклад, на проміжку (0; π).
Якщо x (0; π) ( рис. 69), то при збільшенні аргументу x (x2 > x1) абсциса відповідної точки лінії котангенсів зменшується (тобто ctg x2 < ctgx1), отже, у цьому проміжку функція ctg x спадає. Враховуючи періодичність, робимо висновок, що вона також спадає в кожному з проміжків (πk; π + πk), k Z. ) Проведене дослідження дозволяє побудувати графік функції y = ctg x ана
логічно до того, як було побудовано графік функції y = tg x. Але графік функції у = ctg x можна одержати також за допомогою геометричних перетворень гра
фіка функції у = tg х. За формулою, наведеною на с. 63, tg(2π + x)= − ctgx,
тобто ctgx = − tg(x + 2π). Тому графік функції у = ctg x можна одержати з гра
фіка функції у = tg х паралельним перенесенням уздовж осі Ох на (− 2π)і си
метричним відображенням одержаного графіка відносно осі Ох. Отримуємо графік, який називається котангенсоїдою (рис. 70).
Рис. 70
69
РОЗДІЛ 1. Тригонометричні функції
Приклади розв’язання завдань
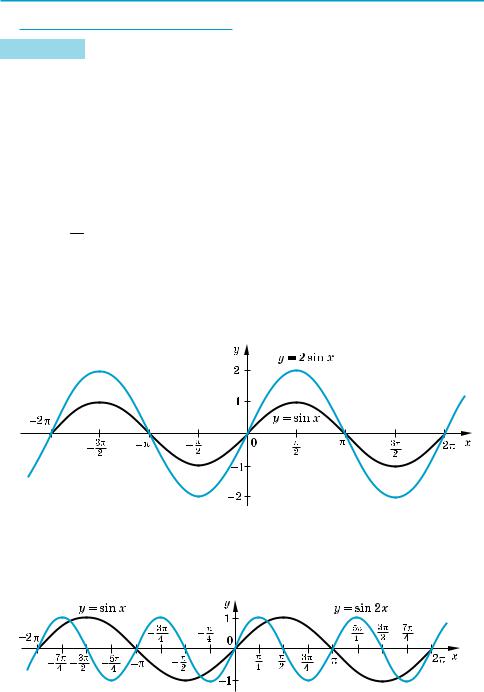
Приклад 1 Побудуйте графік функції та вкажіть нулі функції і проміжки знакосталості: 1) у = 2 sin х; 2) у = sin 2х.
К о м е н т а р Графіки всіх заданих функцій можна одержати за допомогою геометрич
них перетворень графіка функції f (x) = sin х (табл. 4). Отже, графіком кожної із цих функцій буде синусоїда.
1)у = 2 sin х = 2 f (x) — розтягування графіка y = sin x удвічі вздовж осі Оу;
2)у = sin 2х = f (2x) — стискування графіка y = sin x удвічі вздовж осі Ох.
Нулі функції — це абсциси точок перетину графіка з віссю Ох.
Щоб записати проміжки знакосталості функції, зазначимо, що функція у = 2sin х періодична з періодом T = 2π, а функція у = sin 2х періодична з пе
ріодом T = 2π = π. Тому для кожної функції досить з’ясувати на одному періо
2
ді, де значення функції додатні (графік знаходиться вище осі Ох) і де від’ємні (графік знаходиться нижче осі Ох), а потім одержані проміжки повторити через період.
Ро з в ’ я з а н н я
1)X Графік функції у = 2 sin х одержуємо із графіка функції у = sin х роз тягуванням його вдвічі вздовж осі Оу.
Нулі функції: x = πk, k Z.
Проміжки знакосталості: 2 sin x > 0 при x (2πk; π + 2πk), k Z;
2sin x < 0 при x (π + 2πk; 2π + 2πk), k Z. Y
2)X Графік функції у = sin 2х одержуємо із графіка функції у = sin х стис куванням його вдвічі вздовж осі Ох.
70
