algebra10_нелін_дворівн
.pdf

§ 18. Застосування властивостей функцій до розв’язування рівнянь
Якщо функція має декілька проміжків зростання і спадання, то доводиться розглядати кожен з них окремо.
Приклад Розв’яжемо за допомогою теореми 2 рівняння x3 + x = 2 .
x |
|
||
X Спочатку слід урахувати його ОДЗ: x ≠ 0 і згадати, що функція y = |
2 |
на |
|
x |
|||
|
|
||
всій області визначення не є ні спадною, ні зростаючою (с. 22), але вона спа$ дає на кожному з проміжків (–×; 0) і (0; +×). Тому розглянемо кожен з цих проміжків окремо.
1) При x > 0 задане рівняння має корінь x = 1 (13 + 1 = 2 , 2 = 2).
1
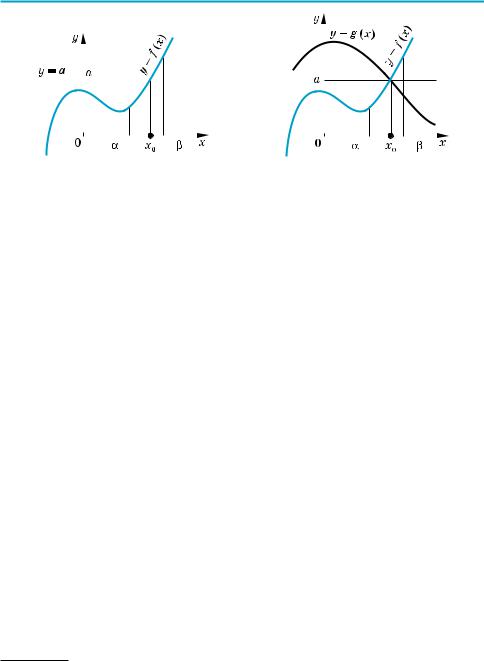
Функція f (x) = x3 + x зростає при x > 0 (як показано вище, вона зростає на
множині R), а функція g (x) = 2x спадає на проміжку x > 0. Отже, задане рівняння f (x) = g (x) при x > 0 має єдиний корінь x = 1.
((−1)3 + (−1) = 2 , − 2= − 2).
−1
Функція f (x) = x3 + x зростає при x < 0, а функція g (x) = 2x спадає на цьому
проміжку. Тому задане рівняння f (x) = g (x) при x < 0 має єдиний корінь x = –1.
У відповідь слід записати всі знайдені корені (хоч на кожному з проміжків корінь єдиний, але всього коренів — два). Oтже, задане рівняння має тільки два корені: 1 і –1. Y
|
Приклади розв’язання завдань |
|
|
|
|
||||||||
|
|
|
|
|
|
Розв’яжіть рівняння x4 + |
1 |
= 2 − (x − 1)2 . |
|||||
Приклад 1 |
|
|
|||||||||||
|
|
4 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Р о з в ’ я з а н н я |
|
|
К о м е н т а р |
|||||||
|
|
|
|
|
|||||||||
X ОДЗ: х ≠ 0. На ОДЗ x4 > 0. Тоді |
|
Якщо розкрити дужки і звести |
|||||||||||
функція f (x) = x4 + |
1 |
l2 (як сума |
обидві частини рівняння до спільно$ |
||||||||||
го знаменника, то для знаходження |
|||||||||||||
4 |
|||||||||||||
|
|
|
|
|
|
|
x |
коренів одержаного рівняння дове$ |
|||||
двох взаємно обернених додатних чи$ |
|||||||||||||
сел), а функція g(x) = 2 − (x − 1)2 m2. |
деться розв’язувати повне рівняння |
||||||||||||
Отже, задане рівняння рівносильне |
восьмого степеня, усі корені якого ми |
||||||||||||
не зможемо знайти. |
|||||||||||||
|
|
|
|
1 |
|
|
|
|
|||||
|
4 |
|
|
|
|
|
Спробуємо оцінити області зна$ |
||||||
|
x |
+ x4 |
= 2, |
|
З другого рів$ |
|
|||||||
|
|
|
чень функцій, які стоять у лівій і пра$ |
||||||||||
системі |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
|
|
вій частинах рівняння. Оскільки на |
|||
|
2 |
− (x −1) = 2. |
|||||||||||
няння системи одержуємо x = 1 , що |
ОДЗ (х ≠ 0) x4 > 0, то в лівій частині |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
203 |
|
|
|||||