
algebra10_нелін_дворівн
.pdfª. П. Нел³н Алгебра ³ початки анал³зу
Двор³вневий п³дручник для 10 класу
загальноосв³тн³х навчальних заклад³в
Рекомендовано М³н³стерством осв³ти ³ науки Укра¿ни
Харк³в «Св³т дитинства»

УДК 373: [512 + 517] ББК 22.12я721 + 2.161я721
Н49
Рекомендовано Міністерством освіти і науки України
(лист № 1/11–3169 від 29 червня 2004 р.)
Ре ц е н з е н т и:
М.І. Бурда, член кореспондент АПН України, доктор педагогічних наук, про
фесор, заступник директора Інституту педагогіки АПН України В. О. Золотарьов, доктор фізико математичних наук, професор, завідувач кафед ри вищої математики та інформатики Харківського національ
ного університету ім. В. Н. Каразіна О. М. Роганін, учитель математики вищої категорії, учитель методист Пісо
чинського колегіуму Харківського району Харківської області
Х у д о ж н и к С. Е. Кулинич
У м о в н і п о з н а ч е н н я в п і д р у ч н и к у
головне в навчальному матеріалі
X початок розв’язання задачі
Y закінчення розв’язання задачі
( початок обґрунтування твердження
) закінчення обґрунтування твердження
Нелін Є. П.
Н49 Алгебра і початки аналізу: Дворівневий підруч. для 10 кл. загально освіт. навч. закладів.— 2 ге вид., виправ. і доп. — Х.: Світ дитинства, 2006.— 448 с.
ISBN 966 544 385 2.
УДК 373: [512 + 517] ББК 22.12я721 + 2.161я721
ISBN 966 544 385 2
©Є. П. Нелін, 2004
©Є. П. Нелін, 2006, з доповненнями
©НМЦ «Світ дитинства» ООО,
оригінал макет, художнє оформлення, 2006
Передмова для учнів
Ви починаєте вивчати новий предмет «Алгебра і початки аналізу», який об’єднує матеріал кількох галузей математичної науки. Як і в курсі алгебри, значну увагу буде приділено перетворенням виразів, розв’язуванню рівнянь, нерівностей та їх систем і розгляду властивостей функцій. Поряд із розв’язу ванням знайомих задач, пов’язаних з многочленами, раціональними дроба ми, степенями і коренями, у 10 класі буде розглянуто нові види функцій: три гонометричні, показникові і логарифмічні та відповідні рівняння і нерівності.
Принципово нова частина курсу — початки аналізу — буде розглядатися в 11 класі. Математичний аналіз (або просто аналіз) — галузь математики, сформована в XVIII столітті, яка відіграла значну роль у розвитку природо знавства: з’явився потужний, досить універсальний метод дослідження функ цій, що виникають під час розв’язування різноманітних прикладних задач.
Кілька зауважень про те, як користуватися підручником.
Система навчального матеріалу підручника з кожної теми представлена на двох рівнях. Основний матеріал наведено в параграфах, номери яких позна чено синім кольором. Додатковий матеріал (номери параграфів позначено сірим кольором) призначений для оволодіння темою на більш глибокому рівні і може опановуватися учнем самостійно чи під керівництвом учителя при ви вченні математики в класах універсального або природничого профілів, а може використовуватися для систематичного вивчення поглибленого курсу алгеб ри і початків аналізу в класах, школах, ліцеях і гімназіях фізико математич ного профілю.
На початку багатьох параграфів наводяться довідкові таблиці, які містять основні означення, властивості та орієнтири по пошуку плану розв’язуван ня задач з теми. Для ознайомлення з основними ідеями розв’язування задач наводяться приклади, у яких, крім самого розв’язання, міститься також ко( ментар, що допоможе скласти план розв’язування аналогічного завдання.
З метою закріплення, контролю і самоконтролю засвоєння навчального матеріалу після кожного параграфа пропонується система запитань і вправ. Відповіді на ці запитання і приклади розв’язування аналогічних вправ мож на знайти в тексті параграфа. Система вправ до основного матеріалу подана на трьох рівнях. Задачі середнього рівня позначені символом «°», дещо складніші задачі достатнього рівня подано без позначень, а задачі високого рівня складності позначені символом «*». В підручнику і для багатьох задач поглибленого рівня пропонуються спеціальні орієнтири, які дозволяють опа нувати методи їх розв’язування. Відповіді і вказівки до більшості вправ на ведено у відповідному розділі. Про походження понять, термінів і символів ви зможете дізнатися, прочитавши «Відомості з історії». У кінці підручника на ведено довідковий матеріал.
3
Передмова для вчителя
Пропонований підручник спрямовано на реалізацію основних положень концепції профільного навчання в старшій школі, на організацію особистіс но орієнтованого навчання математики. Підручник підготовлено відповідно до діючої програми з алгебри і початків аналізу для 10–11 класів з урахуван ням програми з алгебри і початків аналізу для 10–12 класів.
Відзначимо основні відмінності пропонованого підручника від інших підруч ників з алгебри і початків аналізу.
Це дворівневий підручник, який містить загальний матеріал для класів універсального, природничого та фізико математичного профілів і додатко вий матеріал для класів фізико математичного профілю. У кожному розділі поряд з параграфами, які призначені для оволодіння учнями стандартом ма тематичної освіти на академічному рівні, є систематичний матеріал, призна чений для організації індивідуальної роботи з учнями, що цікавляться мате матикою. Запропонований додатковий матеріал може використовуватися і для організації навчання алгебри і початків аналізу в профільних класах фізико математичного профілю або в спеціалізованих школах і класах з по глибленим вивченням математики.
Основний матеріал, який повинні засвоїти учні, структуровано у формі довідкових таблиць на початку параграфа, які містять систематизацію тео ретичного матеріалу та способів діяльності з цим матеріалом у формі спе ціальних орієнтирів по розв’язуванню завдань. У першу чергу учні повинні засвоїти матеріал, який міститься в таблицях. Тому при поясненні ново го матеріалу доцільно використовувати роботу з підручником за відповідни ми таблицями та рисунками. Усі потрібні пояснення й обґрунтування теж наведено в підручнику, але кожен учень може вибирати свій власний рівень ознайомлення з цими обґрунтуваннями. У кожному розділі розв’язанню вправ передує виділення загальних орієнтирів по розв’язуванню таких завдань. Тому важливою складовою роботи за пропонованим підручником є обговорення вибору відповідних орієнтирів та планів розв’язування завдань. Пояснення методів розв’язування ведеться за схемою:
Р о з в ’ я з а н н я |
|
|
К о м е н т а р |
|
|
|
|
Як можна записати |
|
|
Як можна міркувати при |
розв’язання задачі |
|
|
розв’язуванні такої задачі |
|
|
|
|
При такій подачі навчального матеріалу коментар, у якому пояснюється розв’язання, не заважає сприйняттю основної ідеї та плану розв’язування завдань певного типу. Це дозволяє учневі, який вже засвоїв спосіб розв’язу вання, за допомогою наведеного прикладу згадати, як розв’язувати завдан ня, а учневі, якому потрібна консультація по розв’язуванню, — отримати таку детальну консультацію, що міститься в коментарі.
4

За рахунок чіткого виділення загальних орієнтирів роботи з практичними завданнями курсу вдається частину «нестандартних» (з точки зору традицій них підручників) завдань перевести в розряд «стандартних» (наприклад, рівняння, для розв’язування яких доводиться використовувати властивості функцій). Це дозволяє зменшити розрив між рівнем вимог державної атес тації з алгебри і початків аналізу та рівнем вимог з цього курсу на вступних іспитах до вузів, а також ознайомити учнів з методами розв’язування зав дань, які пропонуються на вступних іспитах до вузів.
Зауважимо, що детальна систематизація за змістовними лініями навчаль ного матеріалу та відповідних способів діяльності по розв’язуванню завдань курсу міститься також у посібнику Є. П. Неліна «Алгебра в таблицях. На вчальний посібник для учнів 7–11 класів».— Харків: Світ дитинства, 1998– 2005, який доцільно використовувати в навчальному процесі в комплекті з підручником.
Позначення, які зустрічаються в підручнику
N — множина всіх натуральних чисел
Z — множина всіх цілих чисел Z0 — множина всіх невід’ємних
цілих чисел
Q — множина всіх раціональ них чисел
R — множина всіх дійсних чи сел, числова пряма
R+ — множина всіх додатних дійсних чисел
[a; b] — відрізок (замкнений про міжок) з кінцями a і b,
a < b
(a; b) — інтервал (відкритий про міжок) з кінцями a і b,
a < b
(a; b],
[a; b) — напіввідкриті проміжки з кінцями a і b, a < b
(a; +×), [a; +×), (–×; b],
(–×; b) — нескінченні проміжки (–×; +×) — нескінченний проміжок,
числова пряма
| x | — модуль (абсолютна величина) числа x
[x] — ціла частина числа x {x} — дробова частина числа x
f (x) — значення функції f у точці x D (f) — область визначення функції f E (f) — область значень функції f
sin — функція синус cos — функція косинус tg — функція тангенс
ctg — функція котангенс arcsin — функція арксинус arccos — функція арккосинус arctg — функція арктангенс arcctg — функція арккотангенс
a— арифметичний корінь із чис ла a
2k a — арифметичний корінь 2k(го степеня з числа a (k N)
2k+1 a — корінь (2k+1)(го степеня з числа a (k N)
loga — логарифм за основою a
lg — десятковий логарифм (лога рифм за основою 10)
ln — натуральний логарифм (лога рифм за основою e)
5

Розділ 1
Тригонометричні функції
§ПОВТОРЕННЯ І РОЗШИРЕННЯ 1 ВІДОМОСТЕЙ ПРО ФУНКЦІЮ
1.1.ПОНЯТТЯ ЧИСЛОВОЇ ФУНКЦІЇ. НАЙПРОСТІШІ ВЛАСТИВОСТІ ЧИСЛОВИХ ФУНКЦІЙ
Та б л и ц я 1
1.Поняття числової функції
Числовою функцією з областю ви! значення D називається залежність, при якій кожному числу x із множи! ни D (області визначення) ставить! ся у відповідність єдине число y.
Записують цю відповідність так: y = f (x).
Позначення і терміни
D (f) — область визначення E (f) — область значень
x — аргумент (незалежна змінна)
y — функція (залежна змінна) f — функція
f (x0)— значення функції f у точці x0
2. Графік функції
Графіком функції f називається множина всіх точок координатної площини з координатами (x; f (x)),
де перша координата x «пробігає» всю область визначення функції, а друга координата — це відповідне значення функції f у точці x.
6
§1. Повторення і розширення відомостей про функцію
Пр о д о в ж. т а б л. 1
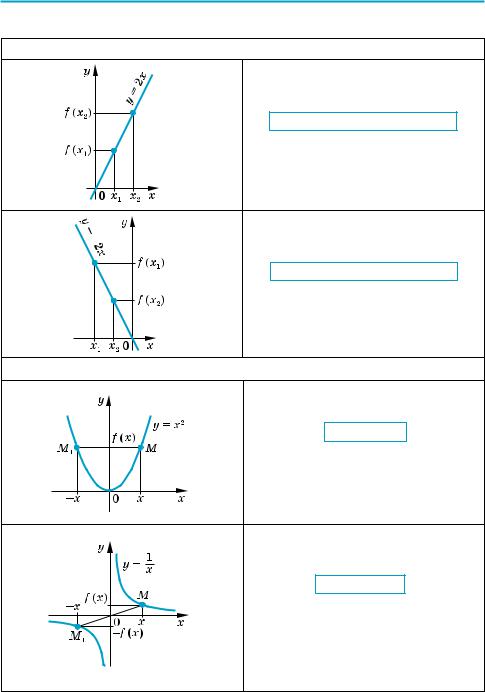
3.Зростаючі та спадні функції
Функція f (x) зростаюча:
якщо x2 > x1, то f (x2) > f (x1)
(при збільшенні аргументу відпо відні точки графіка піднімаються).
Функція f (x) спадна:
якщо x2 > x1, то f (x2) < f (x1)
(при збільшенні аргументу відпо відні точки графіка опускаються).
4. Парні та непарні функції
Функція f (x) парна:
f (–x) = f (x)
для всіх x із області визначення.
Графік парної функції симетричний відносно осі Oy.
Функція f (x) непарна:
f (–x) = –f (x)
для всіх x із області визначення.
Графік непарної функції симет! ричний відносно початку коорди! нат (точки О).
7

РОЗДІЛ 1. Тригонометричні функції
Пояснення й обґрунтування
1. Поняття функції. З поняттям функції ви ознайомилися в курсі алгебри. Нагадаємо, що залежність змінної y від змінної x називається функцією, якщо кожному значенню x відповідає єдине значення y.
У курсі алгебри і початків аналізу ми будемо користуватися таким озна ченням числової функції.
Числовою функцією з областю визначення D називається залежність, при якій кожному числу x із множини D ставиться у відповідність єдине число y.
Функції позначають латинськими (інколи грецькими) буквами. Розглянемо довільну функцію f. Число y, яке відповідає числу x (на рисунку 1 це показано стрілкою), називають значенням функції f у точці x і позначають f (x).
Область визначення функції f — це множина тих значень, яких може на бувати аргумент x. Вона позначається D (f).
Область значень функції f — це множина, яка складається із всіх чисел f (x), де x належить області визначення. Її позначають E (f).
Найчастіше функцію задають за допомогою формули. Якщо немає додат кових обмежень, то областю визначення функції, заданою формулою, вва( жається множина всіх значень змінної, при яких ця формула має зміст.
Наприклад, якщо функція задана формулою y = x + 1 , то її область ви значення: x 0, тобто D (y) = [0; + ), а область значень: y 1, тобто E (y) = [1; + ).
Іноді функція може задаватися різними формулами на різних множинах
x при x 0, значень аргументу. Наприклад, y = x = −x при x < 0.
Функція може задаватися не тільки за допомогою формули, а й за допомо гою таблиці, графіка чи словесного опису. Наприклад, на рисунку 2 графічно
Рис. 1 |
Рис. 2 |
8

§ 1. Повторення і розширення відомостей про функцію
y = | x | |
y =[x] |
|
|
Рис. 3 |
Рис. 4 |
задана функція y = f (x) з областю визначення D (f) = [–1; 3] і множиною зна чень E (f) = [1; 4].
2. Графік функції. Нагадаємо, що
графіком функції y = f (x) називається множина всіх точок координатної площини з координатами (x; f (x)), де перша координата x «пробігає» всю область визначення функції, а друга координата — це відповідне значен! ня функції f у точці x.
На рисунках до пункту 4 таблиці 1 наведено графіки функцій y = x2 та
y = 1 , а на рисунку 3 — графік функції y = | x |. x
Наведемо також графік функції y = [x], де [x] — позначення цілої частини числа x, тобто найбільшого цілого числа, яке не перевищує x (рис. 4). Об ласть визначення цієї функції D (y) = R — множина всіх дійсних чисел, а об ласть значень E (y) = Z — множина всіх цілих чисел.
На рисунку 5 наведено графік ще однієї числової функції y = {x}, де {x} — позначення дробової частини числа x (за означенням {x} = x – [x]).
3. Зростаючі та спадні функції. Важливими характеристиками функцій є їх зростання та спадання.
Функція f (x) називається зростаючою на множині Р, якщо більшому зна!
ченню аргументу з цієї множини відповідає більше значення функції.
Тобто для будь яких двох значень
x1 і x2 з множини Р, якщо x2 > x1, то f (x2) > f (x1).
Наприклад, функція f (x) = 2x зрос таюча (на всій області визначення, тоб то на множині R), оскільки, якщо x2 > x1 , то 2x2 > 2x1 , отже, f (x2) > f (x1).
Рис. 5
9
РОЗДІЛ 1. Тригонометричні функції
у = х3
Рис. 6 |
Рис. 7 |
Рис. 8 |
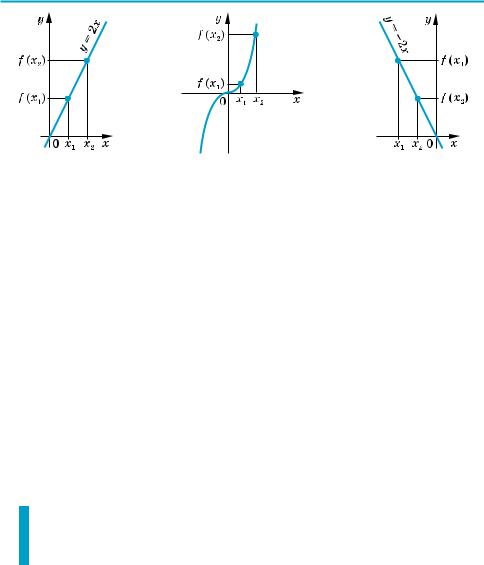
Відповідні точки графіка зростаючої функції при збільшенні аргументу піднімаються (рис. 6).
На рисунку 7 наведено графік ще однієї зростаючої функції у = х3. Дійсно, при x2 > x1 маємо x23 > x13, тобто f (x2) > f (x1).
Функція f(x) називається спадною на множині Р, якщо більшому значен! ню аргументу з цієї множини відповідає менше значення функції.
Тобто для будь яких двох значень x1 і x2 з множини Р, якщо x2 > x1, то
f (x2) < f (x1).
Наприклад, функція f (x) = –2x спадна (на всій області визначення, тобто на множині R), оскільки, якщо x2 > x1, то –2x2 < –2x1, отже, f (x2) < f (x1). Іідповідні точки графіка спадної функції при збільшенні аргументу опуска ються (рис. 8).
Розглядаючи графік функції y = x2 (рис. 9), бачимо, що на всій області визначення ця функція не є ні зростаючою, ні спадною. Але можна виділити проміжки області визначення, де ця функція зростає і де спадає. Так, на про міжку [0; + ) функція y = x2 зростає, а на проміжку (– ; 0] — спадає.
Зазначимо, що для зростаючих і спадних функцій виконуються власти вості, обернені до тверджень, що містяться в означеннях.
Якщо функція зростає, то більшому значенню функції відповідає більше значення аргументу.
Якщо функція спадає, то більшому значенню функції відповідає мен! ше значення аргументу.
(Обґрунтуємо першу з цих властивостей методом від супротивного. Нехай
функція f (x) зростає і f (x2) > f (x1). Припустимо, що аргумент x2 не більше аргументу x1, тобто x2 m x1. З цього припущення одержуємо:
x1 і f (x) зростає, то f (x2) f (x1), що суперечить умові f (x2) > f (x1).якщо x2
Отже, наше припущення неправильне і, якщо f (x2) > f (x1), то x2 > x1, що і потрібно було довести.
Аналогічно обґрунтовується і друга властивість. )
10
