
algebra10_нелін_дворівн
.pdf




РОЗДІЛ 2. Тригонометричні рівняння і нерівності
Запитання для контролю
1.Що називається коренем рівняння? Наведіть приклади.
2.Дайте означення області допустимих значень (ОДЗ) рівняння. Наведіть приклади.
3.Дайте означення рівняння$наслідку даного рівняння. Наведіть приклади. Поясніть, у якому випадку можна гарантувати, що в результаті перетво$ рення рівняння одержали рівняння$наслідок.
4.Дайте означення рівносильних рівнянь. Наведіть приклади. Поясніть, у якому випадку можна гарантувати, що в результаті перетворення рівнян$ ня одержали рівняння, рівносильне заданому.
5.Сформулюйте основні теореми про рівносильність рівнянь. Наведіть при$ клади їх використання.
6.Поясніть, у результаті яких перетворень заданого рівняння можна одер$ жати сторонні для даного рівняння корені. Як можна відсіяти сторонні корені? Наведіть приклади.
7.Поясніть, у результаті яких перетворень заданого рівняння можна втра$ тити корені даного рівняння. Наведіть приклади. Поясніть на прикладах, як необхідно доповнити відповідні перетворення, щоб не втратити корені даного рівняння.
Вправи
1. Знайдіть область допустимих значень (ОДЗ) рівняння:
1) |
x − 5 |
− |
2x − 3 |
= 0; 2) |
2x + 1 |
− |
x |
|
= 0; 3) x = |
3x − 6 |
; 4) |
x2 + 5 − |
x − 5 |
= 0. |
||||||||
|
|
|
||||||||||||||||||||
x + 2 |
|
3 |
x2 + |
|
||||||||||||||||||
|
|
x |
|
|
1 |
|
|
x − 1 |
|
|
|
|
x + 4 |
|||||||||
2. З’ясуйте: а) чи є друге рівняння наслідком першого; |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
б) чи є ці рівняння рівносильними (відповідь обґрунтуйте): |
|||||||||||||||||
1) 2x |
2 |
– 8x – 9 = 0 і x |
2 |
– 4x – 4,5 = 0; |
2) |
x2 − 4 |
= 0 |
і x |
2 |
– 4 = 0. |
||||||||||||
|
|
x2 − 5x + 6 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3.Обґрунтуйте рівносильність рівнянь:
1) 5x – 8 = 7 – 3x і 5x + 3x = 7 + 8; 2) (2x – 1)(x2 + 5) = x(x2 + 5) і 2x – 1 = x.
4.Обґрунтуйте, що задані рівняння не є рівносильними:
1 |
|
1 |
|
|
|
||
1) x2 + |
|
|
= 9 + |
|
|
і x2 = 9; |
2) (2x – 1)(x2 – 5) = x(x2 – 5) і 2x – 1 = x. |
x + |
3 |
x + |
3 |
||||
5.Поясніть, які перетворення було використано при переході від першого рівняння до другого і чи можуть вони приводити до порушення рівносиль$ ності:
1) 3x + 1,1 = 6,8 – 2x і 3x + 2x = 6,8 – 1,1;
2) |
x2 − 81 |
+ 3x2 − 1 = 0 і x – 9 + 3x2 – 1 = 0; |
|||
|
|
||||
|
x + 9 |
|
|
||
3) |
5 |
+ x = 3 |
і 5 + x(3x – 1) = 3(3x |
– 1); |
|
3x − 1 |
|||||
4) |
x2 − 1 = x − 2 і x2 – 1 = x2 – 4x + 4. |
|
|||
|
|
|
|
196 |
|
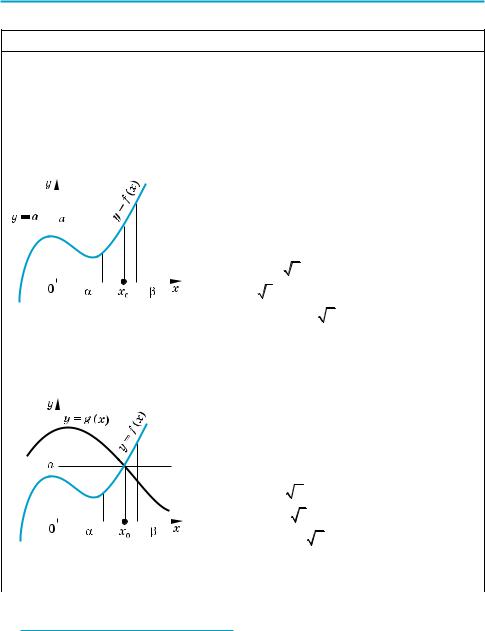


 при розв’язуванні рівняння
при розв’язуванні рівняння