algebra10_нелін_дворівн
.pdf




РОЗДІЛ 4. Показникова і логарифмічна функції
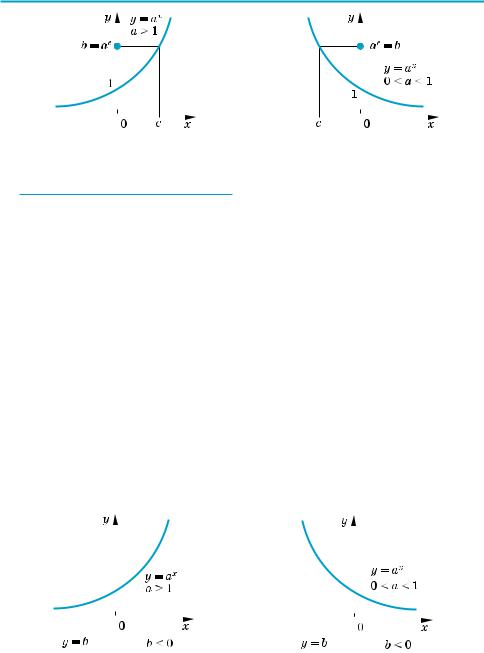
10. Який висновок можна зробити про знак числа х, якщо:
1) 3х = 0,6; 2) (16 )x = 10; 3) 10х = 4; 4) 0,3х = 0,1?
11. Розташуйте числа в порядку їх зростання:
1
1) 23, 2–1,5, 2 2, 2− 2, 21,4, 1;
2) 0,39, 1, 0,3− |
1 |
1 |
5, 0,32 |
, 0,3–9, 0,33. |
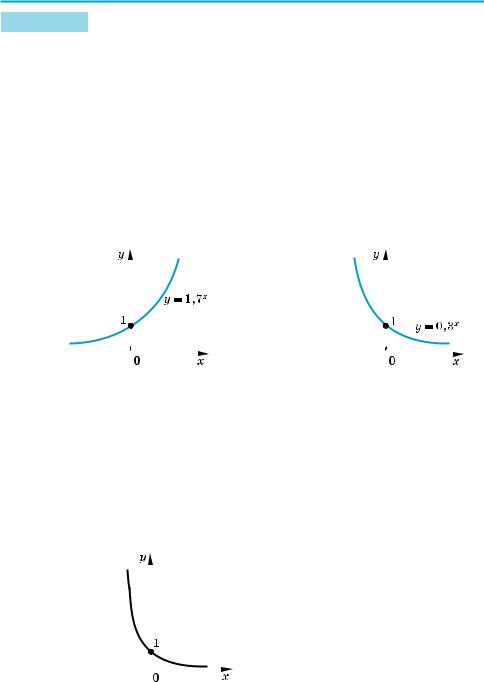
12*. Відомо, що коли при радіоактивному розпаді кількість речовини за добу |
|||||||||
зменшується вдвічі, то через х діб від маси М0 залишається маса М, яка |
|||||||||
обчислюється за формулою: M = M |
( |
1 |
)x . Звідси |
M |
= ( |
1 |
)x . |
|
|
|
M |
|
|
|
|||||
0 |
2 |
|
2 |
|
|
|
|||
|
|
|
|
0 |
|
|
|
|
|
Покажіть графічно, як із зміною х змінюється відношення |
M |
. |
|||||||
|
|||||||||
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
0 |
|
Використовуючи у випадку необхідності побудований графік, дайте відповіді (точні або наближені) на запитання:
а) У скільки разів зменшиться маса радіоактивної речовини через 1,5 доби, 2,5 доби, 3 доби, 4 доби?
б) Скільки часу повинно минути, щоб початкова маса радіоактивної ре& човини зменшилася в 2,5 раза, у 3 рази, у 4 рази?
§30 |
РОЗВ’ЯЗУВАННЯ ПОКАЗНИКОВИХ РІВНЯНЬ |
||||
ТА НЕРІВНОСТЕЙ |
|
|
|||
30.1. НАЙПРОСТІШІ ПОКАЗНИКОВІ РІВНЯННЯ |
|
||||
|
|
|
|
|
Т а б л и ц я 50 |
|
|
|
1. Основні формули та співвідношення |
|
|
|
|
|
|
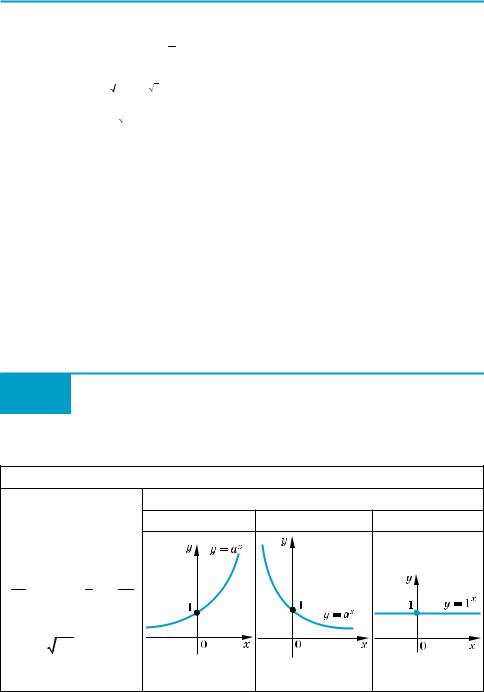
Графік функції y = ax (a > 0) |
|
|
|
|
a > 1 |
0 < a < 1 |
a = 1 |
|
auæav = au + v |
|
|
||
|
(ab)u = auæbu |
|
|
||
au |
= au−v, |
(a )u |
= au |
|
|
av |
|
b |
bu |
|
|
|
(au)v = auv |
|
|
|
|
|
|
m |
|
|
|
|
n am = a n |
|
|
|
|
|
|
|
зростає |
спадає |
стала |
|
|
|
|
338 |
|