Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Криворожский национальный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

algebra10_нелін_дворівн

.pdf

Скачиваний:

Добавлен:

22.03.2015

Размер:

5.24 Mб

Скачать

☆

<<< < Предыдущая 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 4142 / 4542 43 44 45 > Следующая >>>

§ 35. Показникові та логарифмічні рівняння і нерівності

Нерівності із змінною x в останній сукупності систем виконуватимуться для будь&яких значень x за умов:


a > 10,			7,5 < a <10,
a > 10,
		або		5	− a		< −1,
	− a			5	− a

5		< −1			2
	2		5		−	a	> 1.
						a

					2
					2

a > 10,	7,5 < a < 10,
a > 10,
Тобто	або a > 7,
a > 12
	a < 8.

Тоді a > 12 або 7,5 < a < 8. Відповідь: при а (7,5; 8) (12; + ).

Приклад 8 При яких значеннях параметра a рівняння log2 (4x – a) = x має єдиний корінь?

К о м е н т а р

Виконуючи рівносильні перетворення заданого рівняння, як завжди, вра& ховуємо, що при використанні означення логарифма для розв’язування цьо& го найпростішого логарифмічного рівняння його ОДЗ враховується автома& тично.

При виконанні заміни змінної в завданні з параметром враховуємо, що після заміни вимога задачі може змінитися.

Досліджуючи розміщення коренів квадратного тричлена f (t) = t2 – t – a, застосовуємо умови, наведені на с. 225 у таблиці 37 (для запису відповідних умов використаємо позначення: D — дискримінант, t0 — абсциса вершини параболи). Як відомо, для того щоб корені квадратного тричлена f (t) (з до! датним коефіцієнтом при t2) були розміщені по різні боки від числа A, необ!

хідно і достатньо виконання умови f (A) < 0.
Р о з в ’ я з а н н я
Задане рівняння рівносильне рівнянню
4x – a = 2x.	(1)
Тобто 22x – a = 2x. Заміна 2x = t (t > 0) дає рівняння:
t2 – t – a = 0.	(2)

Вимога задачі буде виконуватися тоді і тільки тоді, коли рівняння (2) ма& тиме єдиний додатний корінь. Це буде в одному з двох випадків:

1)рівняння (2) має єдиний корінь, і він додатний;

2)рівняння (2) має два корені, з яких тільки один додатний, а другий — від’ємний або нуль.

	D = 0,		1 + 4a = 0,
Для першого випадку одержуємо	D = 0,				= 1	> 0.
Для першого випадку одержуємо	t	> 0,	тобто t		= 1	> 0.
	0			0	2
					2

Отже, a = − 1.

411

РОЗДІЛ 4. Показникова і логарифмічна функції

Для другого випадку значення t = 0 дослідимо окремо.

При t = 0 з рівняння (2) одержуємо a = 0. При a = 0 рівняння (2) має корені t1 = 0, t2 = 1. Отже, умова задачі при a = 0 виконується.

Залишається ще один випадок — корені рівняння (2) мають різні знаки (розміщені по різні боки від нуля). Це буде тоді і тільки тоді, коли буде вико& нуватися умова f (0) < 0 (де f (t) = t2 – t – a), тобто умова –a < 0, отже, a > 0. Об’єднуючи всі одержані результати, маємо відповідь.

Відповідь: при a = − 1 або a l 0 задане рівняння має єдиний корінь.

Запитання для контролю

1.Поясніть на прикладах, як можна використати властивості функцій до розв’язування показникових та логарифмічних рівнянь.

Вправи

Розв’яжіть рівняння (1–5).

1.	1)	22x = 5 – x;			2) (		2		)x +	(	3	)x = 1;	3) 3x + 4x = 5x;				4) 2x + 2−x = 2cos			x	;
1.	1)	22x = 5 – x;			2) (				)x +	(		)x = 1;	3) 3x + 4x = 5x;				4) 2x + 2−x = 2cos				;
						5				5							3
	5)	log3 (x + 5) = log1 x + 4;										6) log2 (3x + 4) = 2 – 5x;						7) log2 \| x \| = 5 – x2;
					2
	8) log		2	(1 + x2) = log		2		x + 2x – x2;					9)	log x = 1− x2 .
			2			2								5
2.	1) ( 4 − 15 )x + ( 4 + 15 )x = 8;												2) ( 3 + 8 )x + ( 3 − 8 )x = 6;
	3) ( 2 − 3 )x + ( 2 + 3 )x = 2x.
3.	1)	log22 x + (x − 1)log2 x = 6 − 2x;											2) x2 + (x – 3) log2 x = 4x – 3;
	3)	2 lg2 (2x – 1) = lg2 (2x + 1) – lg (2x – 1)ælg (2x + 1).
4.	1) 2\| x + 2 \| – \| 2x + 1 – 1 \| = 2x + 1 + 1;												2)		2 + log1 x	+ 3 =		1 + log5 x	.
4.	1) 2\| x + 2 \| – \| 2x + 1 – 1 \| = 2x + 1 + 1;												2)		2 + log1 x	+ 3 =		1 + log5 x	.
															5
5.	1) 25x – (a – 1)æ5x + 2a + 3 = 0;												2)		4x − 6 2x + 1 = 2x − a.
6.	Розв’яжіть систему рівнянь:

x + 2x = y + 2y, 1)

x2 + 3y = 10;

log2 x − log2 y = y − x, 2) x3 + y3 = 54.

7.Знайдіть всі значення параметра a, при яких рівняння 4x + aæ2x + 1 – а = 0 не має коренів.

8.Знайдіть всі значення параметра a, при яких нерівність aæ9x + 4(a – 1)æ3x + a > 1 виконується при всіх x.

412

Додаткові вправи до розділу 4

9.Знайдіть всі значення параметра a, при яких рівняння 3x + 3–x = 2 cos x + a + 4 має єдиний корінь.

10.Знайдіть всі значення параметра a, при яких рівняння log3 (9x + a) = x має єдиний корінь.

11.Для кожного значення параметра a визначіть число коренів рівняння | lg x | = –(x – 1)2 + a.

12.	Скільки розв’язків має рівняння (log2 (x +1) − 3) x − a = 0 залежно від
	значення параметра a?
13.	Знайдіть всі значення параметра a, при яких система рівнянь
	lg(4 + y) = lgx,


	a − y = 1 (x + a)2 має розв’язки.
		2

ДОДАТКОВІ ВПРАВИ ДО РОЗДІЛУ 4

Обчисліть (1–4).

																									9 log162+log3		5;		3) 81 0,5log97;									10 2+		1
1.	1)	10 log						2	log				2					2 ;				2)			9 log162+log3		5;		3) 81 0,5log97;							4)		10 2+		2 lg16 .
																											4				−	20
2.		4		25		−3log				0,1		+		64			log		5	;							4		5		−	3	+ log4 9			log3 4		− 7	log	3	;
	1)								5									4									2)													7
	1)																	4									2)
																											5 25
	3)	16(log						9	45 − 1)						log					9 log					5	121;	4) (15		+		3 1+ log3 4 ) log 3 log 4;
								9										11							5											2		3
	5)	(30 −5 1+log5 4 ) log																2	5 log						5	4.
																		2							5
3.	1)		log2 66				− log				2		3;														2) log	7,3			5 8 :log				20	8;
3.	1)						− log						3;														2) log				5 8 :log					8;
			log6 66																														7,3
			log6 66
	3)	log				27 − 2log									3 + log								2	;			4) log			34 – log					17 + log			18.
	3)	log			2	27 − 2log								2	3 + log							2 3		;			4) log	6		34 – log				6	17 + log		6	18.
					2									2								2 3						6						6			6
						1																								1	1
																		1									2) (81 4 − 2 log9 4 + 25log125 8 ) 49log7 2;
4.	1)	202 log81 5 (0,25)																1			;
4.	1)	202 log81 5 (0,25)														2 log81 5					;
	3)	490,5(log7 9−log7 6)												−16 5− log 5 4.

5.1) Знайдіть

2) Знайдіть

			a	4			b = –5.
log			a		, якщо log
log	1				, якщо log
b−	4	b6				a

logb5 (a5b5 ), якщо loga b = 5.

413

РОЗДІЛ 4. Показникова і логарифмічна функції

3)Знайдіть logb6 (a6b6 ), якщо loga b = 6.

4)Знайдіть lg 800, якщо lg 2 = 0,301.

6.1) Знайдіть log15 81, якщо log75 3 9 = a.

2)Знайдіть log4 20, якщо lg 2 = a.

3)Знайдіть log70 32, якщо log70 5 = a, log70 7 = b.

4)Знайдіть log30 12, якщо log24 3 = a, log24 5 = b.

Порівняйте значення заданих числових виразів (7–8).

7.	1)	log0,5		7		і log0,125													7		;		2) log0,25									5		і	log0,5					5	;
7.	1)	log0,5				і log0,125															;		2) log0,25											і	log0,5					16	;
			4															164													256									16
						1										1		3													1						1								2log25+ log1 9
		11 і 9 2					log						1+			9 )		3	log		2							15		і 8 3 log2(1−															2log25+ log1 9
	3)	11 і 9 2										3 (				9 )		2		8	;		4)					15		і 8 3 log2(1−						32 ) 2log27 3; 5)								8 і 2				2 .
8.	1)	7 log5 2 − 0,1 і 2 log57;																					2) 5 log37 + 0,1 і 7 log35;																			3) 2 log7 3 + 0,1 і 3 log7 2.
	Знайдіть область визначення функції (9–10).
9.	1)	y =	log2				(			x			2								)				2) y =								(		2	− 4x −					)
9.	1)	y =	log2							x				− 2x − 2 ;											2) y =						log4				x	− 4x −					4 ;
	3)	y =	log1				(			3x				2		−			)						4) y =										(		x	2			)
	3)	y =	log1							3x						−		2x		;					4) y =						1 − log4						x		− 3x .
						2
10.	1)	f (x) =				2 31−x + 1− 3x ;																			2) f (x) = lg((1,25)1−x2																− (0,4096)1+ x );
	3)	f (x) =				27x − 9x2 +0,5 ;																			4) f (x) =								( 4 − x)(3x − 9).
11.	Знайдіть множину значень функції:
																		300																									+	2
																		300																								30	+	4 + log4 x
	1)	y = log0,1																							;									2) y = log0,25														;
	1)	y = log0,1							1			+ lg (									+ x		2 )		;									2) y = log0,25										2				;
																	100				+ x													4) y = log1 (													).
																	24																									10 + log7 (7 +			x	)
																	24
	3)	y = log0,5																					;


						11 +											1 +			ln x																					7			77
						11 +											1 +																								7
	Розв’яжіть рівняння (12–13).
12.	1)	25х – 1æ34x + 1æ73x + 3 = 504х –2;																																2) 29х + 9æ37x + 3æ56x = 720x + 3;
	3)	213 – хæ311 – 2xæ59 – 3x = 360x + 2;																																4) 32х + 3æ33x + 1æ625x + 2 = 600x + 7.
13.	1)	3log6 (3 −											3				)= 4log6 (2 +											1			)+ 3;
13.	1)	3log6 (3 −						2x +							3		)= 4log6 (2 +											x + 1			)+ 3;
								2x +							3													x + 1
	2)	2 log				(x +							6				)= 3 log							(			3		−		2		)+ 5;
	2)	2 log				(x +					x −				5		)= 3 log							(		x			−				)+ 5;
			12								x −				5							12				x	− 2 x − 3
	3)	33 +				8							=							( 3			x	2 )							4)			7 −				1			= 2log4		(	)
																				( 3				2 )																			(	)
					logx 4										3log4						4					;																		0,5 x .
					logx 4																															logx 4

414

Додаткові вправи до розділу 4

14.

При яких значеннях а вираз (1 −

)log5 (1−

)−

a−1

більший за вираз

0,2

4−a2−log

(1+x2−2

)

при всіх допустимих значеннях х?

15.

При яких значеннях а сума log

4 + 3

та log

6 + 5

буде більшою

1 +

a 1

за одиницю при всіх х?

16.При яких значеннях а сума loga (sin x + 2) та loga (sin x + 3) буде до& рівнювати одиниці хоча б при одному значенні х?

17.При яких значеннях а сума loga (cos2 x + 1) та loga (cos2 x + 5) буде дорів& нювати одиниці хоча б при одному значенні х?

18.При яких значеннях а вираз (sinx)lg( sin x)−a2 більший за вираз 10log100(1−cos2 x)+log7 a при всіх допустимих значеннях х?

19.При яких значеннях а вираз (cosx)log3 (cos x)− a більший за вираз

3log9(1−sin2 x)+a(a−2) при всіх допустимих значеннях х?

20. При яких значеннях а вираз (1 − x2 )log4 (1−x2 )− a більший за вираз

0,251− a −log2 1−x2 при всіх допустимих значеннях х?

21.При яких значеннях а вираз (1 − 2x )log2 (1−2x )−2a більший за вираз 0,53− a −log4(1+4x −2x+1) при всіх допустимих значеннях х?

22.Знайдіть усі додатні, не рівні 1, значення а, при яких область визначення функції y = (ax+3 a2 + a4+5loga x − x5+ xlogx a − ( 3 a )27 )0,5 не містить двозначних натуральних чисел.

23.Знайдіть усі значення а, при яких область визначення функції

y = lg (ax+2 x3logx a + a4 x5 − ( x )10+2xlogx a − ( a )18 ) містить тільки одне ціле число.

24.	З області визначення функції y = log3 (aa − a		5x+2	) взяли всі цілі додатні
			x+2
	числа і додали їх. Знайдіть усі додатні значення а, при яких така сума
	буде більшою за 9, але меншою за 13.			) взяли всі цілі додатні
		7x+ 4
25.	З області визначення функції y = log	(aa − a x+ 4
		7

числа і додали їх. Знайдіть усі додатні значення а, при яких така сума буде більшою за 7, але меншою за 11.

415

ДОВІДКОВИЙ МАТЕРІАЛ

Розклад алгебраїчних виразів на множники							Т а б л и ц я 1
							Т а б л и ц я 1

	1. Формули скороченого множення

(a + b)2 = a2 + 2ab + b2						(a – b)2 = a2 – 2ab + b2
	a2 – b2 = (a – b) (a + b)
a3 – b3 = (a – b) (a2 + ab + b2)						a3 + b3 = (a + b) (a2 – ab + b2)
(a + b)3 = a3 + 3a2b + 3ab2 + b3						(a – b)3 = a3 – 3a2b + 3ab2 – b3
(a + b)3 = a3 + b3 + 3ab (a + b)						(a – b)3 = a3 – b3 – 3ab (a – b)

	(a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc
2. Основні прийоми розкладання многочлена на множники

Винесення спільного множника				8a3 + 10a2b3 – 6ab = 2a (4a2 + 5ab3 – 3b)
за дужки
						xy + 3yz – x2 – 3xz =
Спосіб групування						= y (x + 3z) – x (x + 3z) =
						= (x + 3z) (y – x)

Використання формул скороченого				a4 – 64 = (a2)2 – 82 = (a2 – 8) (a2 + 8)
множення

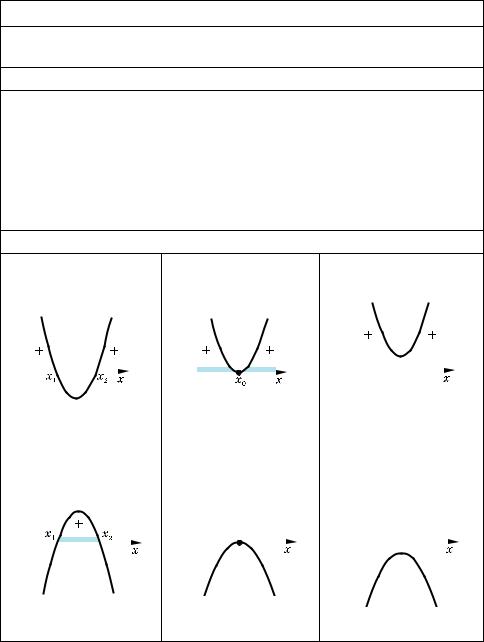
3. Розклад на множники квадратного тричлена ax2 + bx + c (а ≠ 0)

ax2 + bc + c = a (x – x ) (x – x			),	Оскільки 2x2 + 3x – 5 = 0
	1	2
де x1 і x2 — корені квадратного три							5
члена, тобто корені рівняння						при x1 = 1 і x2 = −			, то
члена, тобто корені рівняння						при x1 = 1 і x2 = −		2	, то
ax2 + bc + c = 0				2x	2	+ 3x − 5 = 2(x − 1)(x +	5
				2x		+ 3x − 5 = 2(x − 1)(x +	2)= (x − 1)(2x + 5)
4. Узагальнення деяких формул скороченого множення

an – bn = (a – b) (an – 1 + an – 2b + an – 3b2 + ... + a2bn – 3 + abn – 2 + bn – 1)
П р и к л а д и.	a4 – b4 = (a – b) (a3 + a2b + ab2 + b3)
	a5 – b5 = (a – b) (a4 + a3b + a2b2 + ab3 + b4)
При b =1	an – 1 = (a – 1) (an – 1 + an – 2 + an – 3 + ... + a2 + a + 1)
	Для непарних натуральних п
an + bn = (a + b) (an – 1 – an – 2b + an – 3b2 – ... + a2bn – 3 – abn – 2 + bn – 1)
П р и к л а д и.	a5 + b5 = (a + b) (a4 – a3b + a2b2 – ab3 + b4)
При b = 1 (и n = 2k + 1)
a2k + 1 + 1 = (a + 1) (a2k – a2k – 1 + a2k – 2 – ... + a2 – a + 1)

			416

Системи рівнянь

		Т а б л и ц я 2

1. Системи рівнянь

Поняття системи та її розв’язків		Приклади

Якщо ставиться завдання знай	x − y = 4,
ти всі спільні розв’язки двох (або		— система двох рівнянь
ти всі спільні розв’язки двох (або	2x + y = 11
більше) рівнянь з однією або кілько	2x + y = 11
більше) рівнянь з однією або кілько		з двома змінними.
ма змінними, то кажуть, що потріб		з двома змінними.
ма змінними, то кажуть, що потріб	Пара чисел (5; 1), тобто
но розв’язати систему рівнянь. За	Пара чисел (5; 1), тобто
но розв’язати систему рівнянь. За
писують систему рівнянь, об’єд		x = 5,
нуючи їх фігурною дужкою.		y = 1 — розв’язок системи.
Розв’язком системи називаєть
ся таке значення змінної або такий	x2	− y + z = 0,
впорядкований набір значень
змінних (якщо змінних декілька),	xy + xz + yz = 19, — система трьох
змінних (якщо змінних декілька),
що задовольняє всім рівнянням си	x + y − z = 2
стеми.		рівнянь з трьома змінними.
Роз’язати систему рівнянь —		x = 1,
значить знайти всі її розв’язки або		x = 1,
значить знайти всі її розв’язки або
довести, що розв’язків немає.	Трійка чисел (1; 4; 3), тобто y = 4, —
довести, що розв’язків немає.
Якщо система не має розв’язку,
Якщо система не має розв’язку,		z = 3
то її називають несумісною.		один з розв’язків системи.

2. Рівносильність систем рівнянь

Дві системи рівнянь називають
ся рівносильними на деякій мно
жині, якщо на цій множині вони ма
ють однакові розв’язки (тобто кож	Областю допустимих значень
ний розв’язок першої системи на цій	Областю допустимих значень
ний розв’язок першої системи на цій	(ОДЗ) системи називається спільна
множині є розв’язком другої і, навпа	(ОДЗ) системи називається спільна
множині є розв’язком другої і, навпа	область визначення всіх функцій,
ки, кожний розв’язок другої систе	область визначення всіх функцій,
ки, кожний розв’язок другої систе	що входять до запису цієї системи.
ми є розв’язком першої).	що входять до запису цієї системи.
ми є розв’язком першої).	Всі рівносильні перетворення си
Якщо змінити порядок запису	Всі рівносильні перетворення си
Якщо змінити порядок запису	стем виконуються на ОДЗ початко
рівнянь заданої системи, то одержи	стем виконуються на ОДЗ початко
рівнянь заданої системи, то одержи	вої системи.
мо систему, рівносильну заданій.	вої системи.
мо систему, рівносильну заданій.
Якщо одне з рівнянь системи за
мінити на рівносильне йому рівнян
ня, то одержимо систему, рівносиль
ну заданій.

417

П р о д о в ж . т а б л. 2

3. Основні способи розв’язування систем рівнянь

Спосіб підстановки

Виражаємо з одного рівняння системи одну змінну через іншу (чи через інші) і підставляємо одержаний вираз замість відповідної змінної у всі інші рівняння системи (потім розв’язуємо одержане рівняння чи систему і під ставляємо результат у вираз для першої змінної).

Приклад. Розв’язати систему 2x − y = 3,

x + y = 3.

Ро з в’я з а н н я. З першого рівняння системи у = 2х – 3. Підставляємо

вдруге рівняння системи і одержуємо х + 2х – 3 = 3. Звідси х = 2.

Тоді у = 2х – 3 = 1.

Відповідь: (2; 1).

Спосіб додавання

Якщо перше рівняння системи замінити сумою першого рівняння, по множеного на число α ≠ 0, і другого рівняння, помноженого на число β ≠ 0 (а всі інші рівняння залишити без зміни), то одержимо систему, рівносиль ну заданій.

5x − 3y = 9,		2
5x − 3y = 9,		2
Приклад. Розв’язати систему 3x + 2y = 13.		3

Р о з в’я з а н н я. Помножимо обидві частини першого рівняння систе ми на 2, а другого — на 3 (щоб одержати як коефіцієнти при змінній у протилежні числа) і почленно додамо одержані рівняння. З одержаного рівняння знаходимо значення х, підставляємо результат у будь яке рівнян ня системи і знаходимо значення у.

10x − 6y = 18,

+ = +

9x 6y 39.

19x = 57, x = 3.

Тоді 3æ3 + 2у = 13, 2у = 4, у = 2.

Відповідь: (3; 2).

418

П р о д о в ж . т а б л. 2

Графічне розв’язування систем рівнянь з двома змінними

Виконуємо рівносильні перетворення заданої системи так, щоб зручно було будувати графіки всіх рівнянь, що входять до системи. Потім будує мо відповідні графіки і знаходимо координати точок перетину побудова них ліній — ці координати і є розв’язками системи.

Приклади

2x − y = 3, 1. Розв’язати графічно систему

x + y = 3.

Р о з в’я з а н н я. Задана система рівносильна системі

Графіком кожного з рівнянь системи є пряма.

Для побудови прямої досить побудувати дві її точки. Наприклад, для

у = 2х – 3:	x	0	1

	y	–3	–1
	y	–3	–1

у = 3 – х:	x	0	1
у = 3 – х:	y	3	2
	y	3	2

Графіки перетинаються в єдиній точці М (2; 1). Отже, пара чисел (2; 1) — єдиний розв’язок заданої системи.

Відповідь: (2; 1).

y = 2x − 3,y = 3 − x.

x2 = 2 − y2, 2. Розв’язати графічно систему

x3 − y = 0.

Р о з в’я з а н н я. Задана система рівносильна

x2 + y2 = 2, системі

y = x3.

Графік першого рівняння — коло радіуса 2
з центром у початку координат, а графік друго
з центром у початку координат, а графік друго
го — кубічна парабола у = х3.
Ці два графіки перетинаються в двох точках з								2
Ці два графіки перетинаються в двох точках з								2
координатами (–1; –1) і (1; 1).
Відповідь: (–1; –1), (1; 1) — розв’язок системи.

419

Розв’язування квадратних нерівностей

Т а б л и ц я 3

1. Квадратні нерівності

Квадратною нерівністю називається нерівність виду ax2 + bx + c > 0 (< 0, l 0, m 0), якщо а ≠ 0

Орієнтир

Для розв’язування квадратної нерівності досить знайти корені квад ратного тричлена ax2 + bx + c і побудувати ескіз його графіка (параболу).

Як відповідь записують проміжки осі Ох, для яких точки параболи роз міщені вище від осі Ох (для випадку ax2 + bx + c > 0) і нижче від осі Ох (для випадку ax2 + bx + c < 0).

Якщо квадратний тричлен має два різних корені х1 і х2, то для розв’язу вання нерівності можна також використати метод інтервалів або рівно сильні перетворення нерівності.

2. Різні випадки розв’язування нерівності ax2 + bx + c > 0 (а ≠ 0, D = b2 – 4ac)

a > 0	a > 0	a > 0
D > 0	D = 0	D < 0

x (–×; x ) (х ; +×)

x R (x (–×; +×)

a < 0

D > 0

D = 0

D < 0

x (x1; х2)

Розв’язків немає

420

<<< < Предыдущая 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 4142 / 4542 43 44 45 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.03.20158.49 Mб8978-966-00-1063-5.pdf
#
07.03.2016315.39 Кб16ADMINISTRATIVNO_PRAVOVIJ_STATUS_MON-2.doc
#
07.03.2016359.42 Кб11AGRARNA_POLITIKA_UTsR_DIPLOMNA_ROBOTA.doc
#
21.11.2019178.18 Кб5Alekhina_glava4-97.doc
#
09.11.20194.5 Mб21Alesinskaya_Reshenie_zadach_Ekonom_metody_model...doc
#
22.03.20155.24 Mб60algebra10_нелін_дворівн.pdf
#
07.03.20161.34 Mб214AMMA.doc
#
12.11.20181.63 Mб22Angl.doc
#
30.04.201517.56 Кб45angl.docx
#
22.03.201533.28 Кб278Annotatsia_proizvedenia_Groza.doc
#
22.03.201545.11 Mб46Antichnaya_mifologia_Entsiklopedia.rtf