§ 34. Розв’язування показниково;степеневих рівнянь та нерівностей
При x = 4 рівність (3) виконується (0lg 2 = 0lg 2; 0 = 0 — правильна рівність), отже, x = 4 — корінь рівняння (3).
Якщо | x – 4 | = 1 (тобто x – 4 = 1 або x – 4 = –1, отже, x = 5 або x = 3), рівність (3) теж виконується. При х = 5 і х = 3 одержуємо правильну рівність 1 = 1. Отже, ці числа теж є коренями рівняння (3).
При х ≠ 4, х ≠ 5 і х ≠ 3 на ОДЗ рівняння (3) рівносильне рівнянню
lg (x – 2) = lg (6 – x). Тоді x – 2 = 6 – x, отже, x = 4 — не задовольняє умові
х ≠ 4. Тобто на останній множині рівняння (3) коренів не має.
3.Відмічаємо нулі функції на ОДЗ і зна&
ходимо знак f (x) на кожному з про& міжків, на які розбивається ОДЗ (див. рисунок).
Відповідь: [3; 4] [5; 6).
Приклад 5 Розв’яжіть нерівність xl o ga x+1 > a2x.
К о м е н т а р
На ОДЗ обидві частини нерівності є додатними, тому спробуємо пролога& рифмувати обидві частини нерівності. Оскільки до заданої нерівності вже вхо& дить loga x, то зручно прологарифмувати за основою a. Але при логарифму& ванні за основою, більшою за 1, знак нерівності не змінюється, а при лога& рифмуванні за основою, меншою за 1, знак нерівності змінюється. Доводить& ся розглядати два випадки (у кожному з них одержуємо нерівність, рівно& сильну заданій на її ОДЗ).
Р о з в ’ я з а н н я
ОДЗ: x > 0, a > 0, а ≠ 1.
Прологарифмуємо обидві частини нерівності.
1) При a > 1 задана нерівність на її ОДЗ рівносильна нерівностям: loga (xl o ga x+1 ) > loga (a2x), (loga x + 1) loga x > loga a2 + loga x,
log2a x + loga x > 2 |
+ loga x, log2a x > 2. |
Отже, loga x < − |
|
2 або loga x > 2. |
Тобто loga x < loga a− |
2 або loga x > loga a 2. |
Враховуючи |
ОДЗ (x > 0) і те, що a > 1, одержуємо 0 < x < a− 2 або x > a 2. |
2) При 0 < a < 1 |
задана нерівність на її ОДЗ рівносильна нерівностям: |
loga (xl o ga x+1 )< loga (a2x), |
(loga x + 1) loga x < loga a2 + loga x, |
|
log2a x + loga x < 2 + loga x, |
log2a x < 2. |
|
Отже, − |
2 < loga x < |
2. |
РОЗДІЛ 4. Показникова і логарифмічна функції
Тобто loga a− 2 < loga x < loga a 2.
Враховуючи ОДЗ (x > 0) і те, що 0 < a < 1, одержуємо a 2 < x < a− 2. Відповідь: 1) при a > 1 x (0; a− 2 ) (a 2 ; + ∞ ); 2) при 0 < a < 1 x (a 2; a− 2 ).
Запитання для контролю
1.Поясніть на прикладах, як можна розв’язувати показниково&степеневі рівняння.
2.Поясніть, чому при переході від рівняння xlg x = x2 до рівняння lg x = 2 (основи рівні — прирівняли показники) губиться корінь заданого рівняння.
Вправи
1. Розв’яжіть рівняння: |
|
|
|
|
|
|
|
|
1) xlg x = x3; 2) x2 lg x – 10x = 0; 3) x2l og16 x = |
64 |
; |
|
4) xlogx (x2−3) = 2x; |
|
|
|
|
|
|
x |
|
|
|
х + 2 |
6 |
6) |
|
x − 1 |
|
x2−1 |
= 1; |
|
|
5) х |
= х : а) при x > 0; б) при x R; |
|
|
|
|
|
log3 x+1 − |
1 |
( 2 |
−1 |
) |
7) ( |
1 |
) |
|
|
|
= 2(x − 1); |
|
|
|
|
9 |
|
|
|
|
|
9) 2x2 lg (x – 1) = 1 + (x – 1)3.
2.Розв’яжіть систему рівнянь:
xlog5 y + ylog5 x = 50,
1)log25 x + log25 y = 1,5;
3.Розв’яжіть нерівність:
2
8) 4log4 x + xlog4 x = 8;
xlog2 y + ylog2 x = 16,
2) log2 x − log2 y = 2.
1) |
(x2 − x + 1)x2−2,5x+1 < 1; |
|
|
|
2) |
|
x + 1 |
|
x2−2x l |
|
x + 1 |
|
3 ; |
|
|
|
|
|
|
|
|
|
|
l o g (x−2) |
|
|
l og |
(8−x) |
|
|
|
|
l o g |
x+4 |
4 |
|
|
|
|
3) |
|
x − 2 |
3 |
m |
x − 2 |
3 |
|
; |
4) x |
a |
|
|
|
< a x; |
|
|
|
|
|
|
|
|
5) x3+l o ga x > a2x2.
§35 ПОКАЗНИКОВІ ТА ЛОГАРИФМІЧНІ РІВНЯННЯ І НЕРІВНОСТІ
Деякі показникові та логарифмічні рівняння можна розв’язати, застосо& вуючи властивості відповідних функцій. Нагадаємо основні прийоми, які ви& користовуються при розв’язуванні рівнянь за допомогою властивостей функцій, та наведемо приклади розв’язування рівнянь і нерівностей, що містять показникові, логарифмічні та інші функції.
|
|
|
|
|
|
|
|
|
|
|
|
|
Т а б л и ц я 58 |
|
|
|
|
|
|
|
|
|
|
|
|
Орієнтир |
Приклад |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Скінченна ОДЗ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 x−1 + 3x = 41− 2−2x. |
|
|
|
|
|
x − 1l 0, |
|
|
|
|
x l1, |
|
|
Якщо область допустимих зна$ |
ОДЗ: |
|
|
|
Тоді |
|
чень (ОДЗ) рівняння (нерівності або |
2 − 2x l 0. |
|
|
|
|
x m1. |
|
Отже, ОДЗ: х = 1. |
|
|
|
|
|
|
системи) складається зі скінченно$ |
|
|
|
|
|
|
Перевірка: х = 1 — корінь |
|
го числа значень, то для розв’язу$ |
|
(2 1−1 + 31 = 41− |
2−2, 4 = 4). |
|
вання досить перевірити всі ці зна$ |
|
чення. |
|
|
Інших коренів немає, оскільки до |
|
|
|
|
|
ОДЗ входить тільки одне число. |
|
|
|
|
|
Відповідь: 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Оцінка лівої та правої частин рівняння |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
= cos |
x |
|
|
|
|
|
|
2 |
|
|
. |
|
|
|
|
f (x) = a, |
2 |
|
|
f (x) = g (x) |
|
Оцінимо значення лівої і правої |
|
|
|
|
|
|
|
g (x) = a. |
частин заданого рівняння: |
|
|
f (x) l a |
|
|
|
|
|
|
f (x) = 2x2 l1 (оскільки x2 l 0); |
|
|
g (x) m a |
|
|
якщо g(x) = cos |
x |
, то –1 m g (x) m 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
Якщо потрібно розв’язати рів$ |
Отже, f (x) l 1, g (x) m 1. Тоді задане |
|
|
рівняння рівносильне системі |
|
няння виду f (x) = g (x) і з’ясувало$ |
|
|
|
|
|
|
|
|
|
|
|
ся, що f (x) l a, g (x) m a, то рівність |
|
x2 |
=1, |
|
|
|
|
|
|
2 |
|
між лівою і правою частинами |
|
|
|
|
|
|
|
|
|
|
|
x |
= 1. |
|
можлива тоді і тільки тоді, коли |
|
cos |
|
|
|
|
f (x) і g (x) одночасно дорівню$ |
|
|
2 |
|
|
|
Із першого рівняння одержуємо |
|
ють а. |
|
|
|
|
|
x2 = 0, тобто x = 0, що задовольняє |
|
|
|
|
|
й другому рівнянню. |
|
|
|
|
|
|
|
|
Відповідь: 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
403 |
|
|
|
|
|
|
|
|
РОЗДІЛ 4. Показникова і логарифмічна функції
П р о д о в ж. т а б л. 58
3. Використання монотонності функцій
Схема розв’язування рівняння 1. Підбираємо один або кілька коренів рівняння.
2. Доводимо, що інших коренів це рівняння не має (використовуючи теореми про корені рівняння або оцінку значень лівої та правої час! тин рівняння).
Теореми про корені рівняння
1. Якщо в рівнянні f (x) = a функція f (x) зростає (спадає) на деякому проміжку, то це рівняння може мати не більш ніж один корінь на цьому проміжку.
Приклад
Рівняння 2x + 3х = 5 має єдиний корінь х = 1 (21 + 31 = 5, тобто 5 = 5), оскільки функція f (x) = 2x + 3х зростає (на всій об& ласті визначення х R) як сума двох зро& стаючих функцій.
2. Якщо в рівнянні f (x) = g (x) функція f (x) зростає на деякому проміжку, а функція g (x) спадає на цьому самому проміжку (або навпаки), то це рівняння може мати не більш ніж один корінь на цьому про$ міжку.
Приклад
Рівняння 5x = 27 – x має єдиний корінь х = 2 (52 = 27 – 2, тобто 25 = 25), оскіль& ки f (x) = 5x зростає, а g (x) = 27 – х спадає (при всіх х R).
404

§35. Показникові та логарифмічні рівняння і нерівності
Пр о д о в ж. т а б л. 58
|
|
|
|
|
|
4. «Шукай квадратний тричлен» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Орієнтир |
|
|
|
|
|
|
|
|
|
Приклад |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x – (7 – x)æ2x + 12 – 4x = 0. |
|
|
|
|
|
|
|
|
|
Запишемо, що 4x = 22x, і введемо заміну |
|
|
|
|
|
|
|
|
|
2x = t. Одержуємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 – (7 – x)æt + 12 – 4x = 0. |
|
|
Спробуйте розглянути |
|
|
Розглянемо це рівняння як квадратне віднос& |
задане рівняння як квад$ |
|
|
но t. Його дискримінант |
|
|
|
|
|
|
|
|
|
ратне відносно якоїсь змін$ |
|
|
D = (7 – x)2 – 4(12 – 4x) = x2 + 2x + 1 = (x + 1)2. |
ної (чи відносно якоїсь фун$ |
|
|
Тоді t1,2 |
= |
7 − x ± (x + 1) |
, тобто t |
|
|
|
|
|
кції). |
|
|
|
|
|
|
|
= 4, t |
|
= 3 – x. |
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обернена заміна дає 2x = 4 (звідси x = 2) або |
|
|
|
|
|
|
|
|
|
2x = 3 – x. Останнє рівняння має єдиний |
|
|
|
|
|
|
|
|
|
корінь x = 1, оскільки f (x) = 2x зростає, а |
|
|
|
|
|
|
|
|
|
g (x) = 3 – x спадає (при всіх х R). |
|
|
|
|
|
|
|
|
|
|
Відповідь: 1; 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приклади розв’язання завдань |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’яжіть рівняння ( |
2 − |
3 )x + ( |
2 + |
|
3 )x = 4. |
|
|
|
Приклад 1. |
|
|
|
|
|
|
|
|
Р о з в ’ я з а н н я |
|
|
|
|
|
|
|
|
|
К о м е н т а р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
Помічаємо, що |
|
|
|
|
|
Якщо ( 2 − |
3 ) |
= t, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
2 − 3 ) ( |
|
|
|
|
3 )= |
22 − ( |
3)2 = 1. |
( 2 + |
3 )x = 1. Одержуємо t + |
1 |
= 4. |
|
2 + |
|
|
|
|
|
|
|
|
|
|
|
|
2 − |
3 = a, то |
|
|
|
t |
|
|
t |
|
|
|
Отже, якщо |
|
Отже, t2 – 4t + 1 = 0. Тоді |
|
|
|
|
|
|
2 + 3 = |
1 |
. Тобто задане рівняння |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 = 2 − 3, t2 = 2 + 3. |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
має вигляд a |
|
+ |
|
|
= 4, і його можна |
|
Обернена заміна дає |
|
|
|
|
|
|
a |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
x |
|
|
|
|
|
|
|
розв’язати за допомогою заміни ax = t. |
2 − |
3 ) = 2 − |
3 (звідси x = 2) |
|
Але тепер цю заміну можна безпосе& |
або ( |
|
3 )x = 2 + |
|
|
|
|
|
|
редньо використати для заданого |
2 − |
3 (звідси x = –2). |
|
рівняння, не вводячи проміжні по& |
Відповідь: – 2; 2. |
|
|
|
|
|
|
значення. Після оберненої заміни |
|
|
|
|
|
|
враховуємо, що |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 + 3 = |
|
|
= |
|
|
|
|
|
= ( |
|
2 − 3 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
2 − |
3 |
( |
|
2 − |
|
3 )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

РОЗДІЛ 4. Показникова і логарифмічна функції
|
|
Розв’яжіть рівняння 4x + |
1 |
+ 2x − |
1 |
= 4. |
|
Приклад 2 |
|
x |
x |
|
|
4 |
2 |
|
К о м е н т а р
Якщо звести всі степені до однієї основи 2 і позначити 2x = t, то одержимо рівняння (1) (див. розв’язання), у якому можна ввести заміну t − 1 = u (тоді
|
|
|
|
t |
u2 = t2 − 2 + |
1 |
, отже, t2 + |
1 |
= u2 + 2 . На ОДЗ заданого рівняння (x R) всі |
|
t2 |
|
t2 |
|
заміни і обернені заміни є рівносильними перетвореннями цього рівняння. Отже, розв’язавши рівняння, одержані в результаті замін, і виконавши обер& нені заміни, ми отримаємо корені заданого рівняння.
Р о з в ’ я з а н н я
|
|
|
|
|
|
2x |
+ |
1 |
+ 2 |
x |
− |
1 |
|
= 4. |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2x |
|
|
2 |
x |
Заміна 2x = t дає рівняння |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 + |
1 |
+ t − 1 = 4. |
|
|
(1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
t |
|
|
|
|
|
|
|
|
Позначимо |
1 |
тоді |
|
2 |
|
1 |
|
|
|
|
2 |
|
|
|
|
отже, з рівняння (1) одержуємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t − t = u, |
t |
|
+ t2 |
|
= u + |
2, |
|
|
|
|
|
|
|
|
|
= –2. |
рівняння u2 + u – 2 = 0, яке має корені: u |
1 |
= 1, u |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обернена заміна дає t − |
1 |
= 1 або t − |
1 |
= −2. Тоді t2 – t – 1 = 0 або t2 + 2t – 1 = 0. |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Одержуємо t = |
1 + |
5 |
, t |
= |
|
1 − 5 |
|
|
або |
|
t |
= −1 + |
2, t |
= −1 − |
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
= |
1 |
+ 5 |
|
|
|
|
|
|
|
|
|
1 + 5 |
|
|
|
|
|
x |
= |
1 − 5 |
|
|
|
|
|
|
|
Тоді 2 |
|
|
|
|
|
|
(звідси x = log2 |
|
|
|
|
|
|
або 2 |
|
|
|
( коренів немає, оскіль& |
|
|
2 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − |
5 |
|
|
|
|
, або 2x |
|
|
+ |
|
|
|
|
|
|
|
|
|
x = log |
|
( |
2 − 1)), або |
2x |
|
|
|
|
ки |
|
< |
0 |
|
1 |
2 |
(звідси |
|
= − |
1 |
− |
2 (ко& |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
= − |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
ренів немає, оскільки −1 − |
2 < 0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Відповідь: log2 |
1 + 5 |
; log2 ( |
2 − 1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’яжіть рівняння 4x + |
1 |
= 2cos2x. |
|
|
|
|
|
|
|
Приклад 3 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
Іспосіб
Ко м е н т а р
Враховуючи, що 4x > 0, одержуємо, що в лівій частині рівняння стоїть сума двох взаємно обернених додатних чисел, яка завжди більша або дорівнює 2.
§ 35. Показникові та логарифмічні рівняння і нерівності
|
(Дійсно, якщо a > 0, то a + |
1 |
− 2 = |
a2 − 2a + 1 |
= (a − 1)2 |
l 0, отже, при всіх a > 0 |
|
a |
a |
|
a + |
1 |
l 2.) |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
Для оцінки значень правої частини досить згадати, що областю значень функції cos 2x є проміжок [– 1; 1], отже, –2 m 2 cos 2x m 2.
Р о з в ’ я з а н н я
Оцінимо значення лівої і правої частин рівняння. f (x) = 4x + 1 l 2 як сума
4x
двох взаємно обернених додатних чисел. Якщо g (x) = 2 cos 2x, то –2 m g (x) m 2. Отже, f (x) l 2, g (x) m 2, тоді задане рівняння рівносильне системі
=2 cos 2x 2.
З першого рівняння, використовуючи заміну 4x = t, одержуємо
t + 1 = 2, тобто t2 – 2t + 1 = 0. Звідси t = 1.
t
Тоді 4x = 1, отже, x = 0, що задовольняє й другому рівнянню.
Відповідь: 0.
ІІ спосіб розв’язування рівняння 4x + 1x = 2cos2x
4
К о м е н т а р
Якщо позначити 4x = t, то задане рівняння зводиться до рівняння (2) (див. розв’язання), яке можна розглядати як квадратне відносно змінної t. Заува& жимо, що t = 4x ≠ 0, отже, при таких значеннях t рівняння (1) і (2) є рівносиль& ними. Далі використовуємо умову існування коренів квадратного рівняння.
Р о з в ’ я з а н н я
Після заміни 4x = t (t > 0) із заданого рівняння одержуємо рівносильне рівняння
t + |
1 |
= 2 cos 2x, |
(1) |
|
|
t |
|
яке, у свою чергу, рівносильне рівнянню |
|
t2 – (2 cos 2x) t + 1 = 0. |
(2) |
Розглянемо рівняння (2) як квадратне відносно змінної t. |
|
Тоді його дискримінант D = 4 cos2 2x – 4. |
|
Рівняння (2) може мати корені тільки тоді, коли D l 0, тобто коли |
|
4 cos2 2x – 4 l 0, тоді |
|
cos2 2x l 1. |
(3) |
У цій нерівності знак «більше» не може виконуватися (cos2 2x m 1 завж& ди), отже, нерівність (3) рівносильна рівнянню cos2 2x = 1. Тоді cos 2x = 1 або cos 2x = –1. Підставляючи ці значення в рівняння (2), одержуємо дві системи:
|
РОЗДІЛ 4. Показникова і логарифмічна функції |
cos 2x = 1, |
cos 2x = −1, |
t2 − 2t + 1 = 0 |
або t2 + 2t + 1 = 0. У другій системі з другого рівняння маємо |
t = –1, що не задовольняє умовi t > 0. Отже, задане рівняння рівносильне тільки першій системі. З другого рівняння першої системи маємо t = 1, тоді 4x = 1, тобто x = 0, що задовольняє і першому рівнянню цієї системи.
Відповідь: 0.
Приклад 4 Розв’яжіть рівняння 2| x | – | 2х + 1 – 2 | = 2х + 1.
К о м е н т а р
Для розв’язування рівняння з кількома модулями можемо використати загальну схему (с. 240):
1)знайти ОДЗ;
2)знайти нулі всіх підмодульних функцій;
3)позначити нулі на ОДЗ і розбити ОДЗ на проміжки;
4)знайти розв’язки рівняння в кожному з проміжків.
Р о з в ’ я з а н н я
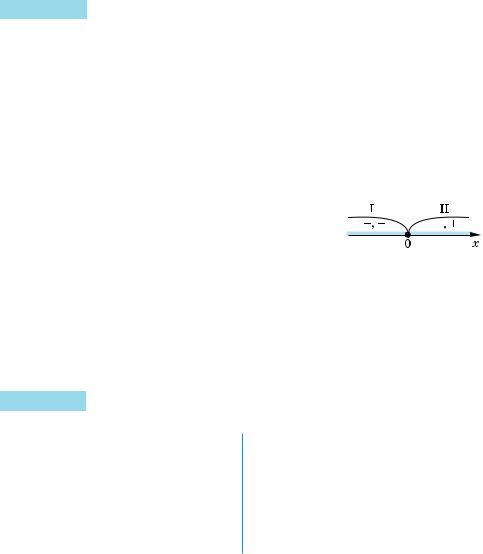
ОДЗ: х R.
Нулі підмодульних функцій: x = 0 і 2x + 1 – 2 = 0, 2x + 1 = 2, x + 1 = 1, x = 0.
Цей нуль (x = 0) розбиває ОДЗ на два проміжки, у кожному з яких кожна підмодульна функція має постійний знак (див. рисунок).
Проміжок І. При x (– ; 0] маємо рівняння 2–x + 2x + 1 – 2 = 2x + 1. Тоді 2–x = 2, отже, x = –1 (– ; 0].
Проміжок ІІ. При x [0; + ) маємо рівняння 2x – (2x + 1 – 2) = 2x + 1. Тоді
2x = |
2 |
, звідси x = log |
|
2 |
. Але log |
|
2 |
< 0, отже, у ІІ проміжку задане рівнян& |
3 |
|
2 3 |
|
2 3 |
|
ня коренів не має.
Відповідь: –1.
Приклад 5 Розв’яжіть рівняння
lg2 (x + 1) = lg (x + 1) lg (x – 1) + 2 lg2 (x –1).
Р о з в ’ я з а н н я
x + 1 > 0,
ОДЗ: x − 1 > 0. Тобто x > 1.
Оскільки x = 2 не є коренем задано& го рівняння, то при діленні обох час& тин рівняння на lg2 (x – 1) ≠ 0 одер&
К о м е н т а р
Якщовиконатизамінуlg (x+1) = u, lg (x – 1) = v, то одержимо рівняння u2 = uv + 2v2, усі члени якого мають однаковий сумарний степінь — два. Нагадаємо, що таке рівняння нази! вається однорідним і розв’язується

§ 35. Показникові та логарифмічні рівняння і нерівності
|
жуємо рівносильне рівняння (на ОДЗ) |
діленням обох частин на найвищий |
|
|
|
lg2 (x + 1) |
|
lg(x + 1) |
|
|
|
|
|
|
степінь однієї із змінних. Розділимо, |
|
|
|
|
|
|
= |
|
|
+ 2. |
|
|
|
наприклад, обидві частини на v2 (тоб& |
|
|
|
lg2 (x − 1) |
lg (x − 1) |
|
|
|
|
Після заміни t = |
|
lg(x + 1) |
маємо |
то на lg2 (x – 1)). |
|
|
lg |
( |
x − |
) |
|
Щоб не загубити корені рівняння |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
при діленні на вираз із змінною, по! |
|
рівняння t |
– t – 2 = 0, корені якого: |
|
|
|
|
|
|
|
|
трібно ті значення змінної, при яких |
|
|
|
|
|
|
t1 = –1, t2 = 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
цей вираз дорівнює нулю, розгляну! |
|
Виконавши обернену заміну, одер& |
|
ти окремо. Значення x, при якому |
|
жуємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lg (x – 1) = 0 (тоді x – 1 = 1), тобто |
|
|
lg(x + 1) |
= −1 або |
lg(x + 1) |
= 2. |
|
|
|
|
|
|
|
|
|
|
x = 2, підставляємо в задане рів& |
|
|
lg (x − 1) |
lg(x − 1) |
|
|
|
Тоді на ОДЗ маємо рівносильні рів& |
няння. |
|
Для реалізації одержаного плану |
|
няння: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
розв’язування не обов’язково вводи& |
|
lg (x + 1) = –lg (x – 1) або |
|
|
|
|
|
|
|
|
|
|
|
|
|
ти змінні u і v, досить помітити, що |
|
|
|
|
|
|
|
|
|
lg (x + 1) = 2 lg (x – 1), |
|
|
|
|
|
|
|
|
|
задане рівняння однорідне, розділити |
|
|
|
|
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
|
|
|
|
|
|
lg (x + 1) = lg (x – 1) |
|
або |
|
|
|
|
2 |
, |
обидві частини на lg2 (x – 1), а вже |
|
|
|
|
|
|
|
|
|
lg (x + 1) = lg (x – 1) |
|
потім увести нову змінну t. |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + 1 = |
|
|
|
або x + 1 = (x – 1)2, |
|
|
У кінці враховуємо, що всі пере& |
|
x |
− 1 |
|
|
|
|
|
|
або x + 1 = x2 – 2x + 1, |
творення були рівносильними на |
|
x2 – 1 = 1 |
|
|
x2 = 2 |
або x2 – 3x = 0, |
|
|
|
ОДЗ, отже, необхідно вибрати тільки |
|
|
x = ± |
|
2 |
|
або x = 0 чи x = 3. |
|
|
ті із знайдених розв’язків, які вхо& |
|
|
|
|
|
|
дять до ОДЗ. |
|
Враховуючи ОДЗ, одержуємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = |
2 або x = 3. |
|
|
|
|
|
|
|
|
|
|
|
|
Відповідь: |
|
|
2; 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Розв’яжіть рівняння log2 (1+ x − 2) + log1 (1− |
|
x2 − 4 |
|
)= 0. |
|
Приклад 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К о м е н т а р |
Логарифмічні функції, які стоять у лівій частині заданого рівняння, набу& вають тільки невід’ємних значень.
Дійсно, на всій області визначення 1 + x − 2 l1, отже, log2 (1+ x − 2 )l0; аналогічно, оскільки 1 – | x2 – 4 | m 1, то на своїй області визначення
log1 (1− x2 − 4 )l0. У цьому випадку сума двох невід’ємних функцій може до!
3
рівнювати нулю тоді і тільки тоді, коли кожна з цих функцій дорівнює нулю.
Зауважимо, що при переході від заданого рівняння до системи рівнянь ОДЗ не змінюється, отже, її можна не записувати в явному вигляді. При роз& в’язуванні одержаних найпростіших логарифмічних рівнянь ОДЗ теж врахо& вується автоматично, тому її можна взагалі не записувати до розв’язання.

РОЗДІЛ 4. Показникова і логарифмічна функції
|
|
|
|
|
|
Р о з в ’ я з а н н я |
Оскільки на всій області визначення log |
2 |
(1+ x − 2 )l0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
і log |
1 |
(1− |
|
x2 − 4 |
|
)l 0, то задане рівняння рівносильне системі |
|
|
|
3 |
|
|
|
|
|
|
( |
|
|
−2 |
) |
= 0, |
|
|
|
|
|
|
log2 |
1 + x |
|
|
|
|
|
|
|
|
log |
|
(1− |
|
x2 |
− 4 |
|
)= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
З першого рівняння системи одержуємо 1+ x − 2 = 20. Тоді x − 2 = 0, тоб& то х = 2, що задовольняє і другому рівнянню системи.
Відповідь: 2.
Приклад 7 При яких значеннях параметра a нерівність
|
|
|
3 cos x + a − 5 |
|
log |
|
|
sinx + |
> 0 |
|
|
5 |
|
2a−15 |
|
|
|
5 |
|
|
|
|
виконується для будь&яких значень x? К о м е н т а р
Спочатку скористаємося формулою a sin x + b cos x = a2 + b2 sin (x + ϕ): sin x + 3 cos x = 2 sin (x + π3 ). Потім запишемо праву частину нерівності як зна&
чення логарифмічної функції і, переходячи до аргументів, врахуємо, що у ви& падку, коли основа цієї функції більша за 1, функція зростає, а коли менша за 1 (але більша за 0) — спадає.
При подальшому аналізі одержаних нерівностей враховуємо, що нерівність sin t > b виконується для будь&яких значень t тоді і тільки тоді, коли b < –1, а нерівність sin t < c — коли c > 1.
Р о з в ’ я з а н н я Задана нерівність рівносильна нерівності
|
|
|
|
|
|
2 sin(x + π )+ a − 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
log |
2a−15 |
|
|
|
|
|
> log |
2a−15 |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
5 |
|
|
Ця нерівність рівносильна сукупності систем |
|
|
|
|
2a − 15 |
> 1, |
|
|
|
|
0 < |
2a − 15 |
< 1, |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 sin(x + π )+ a − 5 |
або |
|
|
2 sin(x + π )+ a − 5 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
> 1 |
0 |
< |
|
|
|
3 |
|
< 1. |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
a > 10, |
|
|
|
|
7,5 < a < 10, |
|
|
|
|
|
π ) |
|
|
|
− a < sin(x + π )< 5 − a . |
Тоді |
|
> 5 − a |
або |
|
sin(x + |
5 |
|
|
|
3 |
2 |
|
2 |
|
|
|
|
3 |
2 |