Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Криворожский национальный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

algebra10_нелін_дворівн

.pdf

Скачиваний:

Добавлен:

22.03.2015

Размер:

5.24 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 4510 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

§ 7. Формули додавання та їх наслідки

Пояснення й обґрунтування

(Формули додавання дозволяють обґрунтувати формули зведення, за яки$

ми тригонометричні функції від аргументів виду kπ äα і (2k + 1) 2π ± α (k Z) зводять до тригонометричних функцій від аргументу α.

Розглянемо декілька прикладів.

sin (π – α) = sin π cos α – cos π sin α = 0æcos α – (–1)æsin α = sin α; cos (π + α) = cos π cos α – sin π sin α = (–1)æcos α – 0æsin α = –cos α;

ctg(6π − α )=	cos(6π − α )	=	cos6πcos α + sin6π sinα	=	cos α	= − ctgα
	sin(6π − α )		sin6πcos α − cos6π sinα		− sin α

(звичайно, в останньому випадку той самий результат можна одержати, використовуючи періодичність і непарність функції котангенс);

sin(

− α )= sin

cosα − cos

sinα = 1 cosα − 0 sinα = cosα;

7π

cos(

+ α )= cos

cosα − sin

sinα = 0 cosα − (−1) sin α = sin α;

tg(

3π

+ α )=

sin

(

3π + α

)

sin 3π cos α + cos 3π sin α

− cos α

= − ctgα.

(

3π

)

3π

sin α

cos

+ α

cos

sin α

cos α − sin

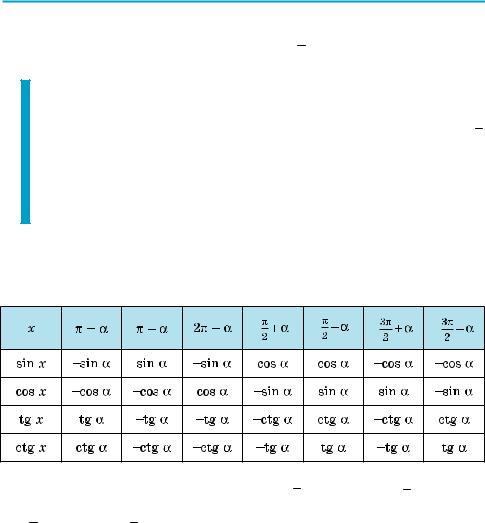
Для аналізу одержаних результатів складемо таку таблицю:

Т а б л и ц я 18

Зміна

Чверть (якщо

Знак заданої

Вид

Одержана

назви

умовно вва$

функції

аргументу

формула

заданої

жати α гост$

у відповідній

функції

рим кутом)

чверті

kπ ä α

sin (π – α) = sin α

немає

cos (π + α) = –cos α

немає

IІI

–

(k Z)

ctg (6π – α) = –ctg α

немає

–

sin(

− α )= cosα

(2k + 1)

± α

7π

)

+ α

= sinα

cos

(k Z)

tg(

3π

+ α )

= − ctgα

–

РОЗДІЛ 1. Тригонометричні функції

Аналогічно можна обґрунтувати, що у всіх випадках тригонометричні

функції від аргументів виду kπ ä α і (2k + 1) π ± α (k Z) можна зводити до

тригонометричних функцій від аргументу α за таким алгоритмом:

якщо до числа α додається число kπ, k Z (тобто число, яке зобра жується на горизонтальному діаметрі одиничного кола), то назва

заданої функції не змінюється, а якщо додається число (2k + 1) 2π

(тобто число, яке зображується на вертикальному діаметрі оди ничного кола), то назва заданої функції змінюється на відповідну (синус на косинус, косинус на синус, тангенс на котангенс і котан генс на тангенс). Знак одержаного виразу визначається знаком по чаткового виразу, якщо умовно вважати кут α гострим. )

У таблиці 19 наведено основні формули зведення. Всі інші випадки мо$ жуть бути зведеними до них за допомогою використання періодичності відпо$ відних тригонометричних функцій.

Т а б л и ц я 19

Зазначимо, що за формулами зведення cos(2π − α )= sin α, sin(2π − α )= cos α,

ctg(2π − α )= tg α, tg(2π − α )= ctg α. Якщо останні формули записати справа на$ ліво, то одержимо корисні співвідношення, які часто називають формулами

2 )

доповняльних аргументів (аргументи α і 2

− α доповнюють один одного до

)

sin α = cos

− α ,

cos

α = sin

− α ,

(

)

(

)

tg α = ctg

− α ,

ctg

α = tg

− α .

Наприклад, sin 60° = cos (90°–60°) = cos 30°; cos 89° = sin (90°–89°) = sin 1°.

§ 7. Формули додавання та їх наслідки

Приклади розв’язання завдань

Приклад 1 Обчисліть за допомогою формул зведення:

1) cos 210°; 2)	tg	3π	.

	4

Ро з в ’ я з а н н я

1)X cos 210° = cos(180° + 30°) =

= − cos 30° = − 3 ;Y

2) X tg 34π = tg(2π + 4π )= −ctg 4π = −1. Y

К о м е н т а р

Подамо задані аргументи так, щоб можна було використати формули зведення (тобто виділимо в аргументі такі частини, які зображаються на го$ ризонтальному або вертикальному діаметрі одиничного кола). Напри$ клад, 210° = 180° + 30°. Звичайно, можна було подати цей аргумент ще й так: 210° = 270° – 60° і теж викорис$ тати формули зведення.

Приклад 2*

Доведіть тотожність

cos(3π − α )

sin(2π + α )

− cos

(

3π

− α)= cos 2α.

(

+ α

)

tg(π + α )

К о м е н т а р

Доведемо, що ліва частина тотожності дорівнює правій. Спочатку викори$ стаємо формули зведення, а потім спростимо одержані вирази, використову$ ючи формули: tg αæctg α = 1 та cos2 α – sin2 α = cos 2α. При спрощенні виразів cos (3π – α) та tg (π + α) можна застосувати як безпосередньо формули зведен$ ня, так і періодичність відповідних функцій. Наприклад, враховуючи, що періодом функції cos x є 2π, одержуємо: cos (3π – α) = cos (2π + π – α) = cos (π – α) = = –cos α.

	cos(3π − α )		sin(	π	+ α )
X	cos(3π − α )		sin(	2	+ α )
X	tg(π	+ α )	tg(π + α )
	2

Ро з в ’ я з а н н я

−cos2 (32π − α )= ((−−cosctgαα))costgαα − (− sinα )2 =

=− cos2 α − sin2 α = cos2 α − sin2 α = cos2α. Y

−1

Запитання для контролю

1.Проілюструйте на прикладах використання формул зведення. Поясніть одержаний результат.

2*. Доведіть декілька формул зведення.

РОЗДІЛ 1. Тригонометричні функції

Вправи

1. Обчисліть за допомогою формул зведення:

1) sin 240°;

2) tg 300°;

)

3) cos 330°;

4) ctg 315°;

(

4 )

5) cos

4π

;

6) sin

−

11π

;

7) tg

7π

;

8) ctg

−

3π

Обчисліть:

1) cos 8° cos 37° – cos 82° cos 53°;

2) sin 68° sin 38° – sin 52° cos 112°.

Спростіть вираз:

sin(

3π

− α )cos(

+ α )

sin(3π + α )sin(

5π

− α )

sin(π + α )cos(π − α )

;

1°)

ctg(

3π

− α )

;

2°)

tg(π − α )

;

3°)

sin(π −

2α )

tg(

3π

− α2)− cos(π − α) sin(3π + α)

; 5 ) tg 1°ætg 2°ætg 3°æ...ætg 87°ætg 88°ætg 89°.

(cos(3,5π − α )+ sin(1,5π + α ))2 − 1

Доведіть тотожність:

1°) 2 sin (90° + α) sin (180° + α) = –sin 2α;

2°) ctg 20°æctg 70° = 1;

sin(π − 2α )−

2sin

(

π − α

)

sin2

+ α

− cos2

α −

)

(

2 )

= −2 ctg α;

4*)

sin2 2α.

(

)

(

2 )

(

cos

− α

− sin2

tg2

+ α

− ctg2

α −

7.4.ФОРМУЛИ СУМИ І РІЗНИЦІ ОДНОЙМЕННИХ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ ТА ФОРМУЛИ ПЕРЕТВОРЕННЯ ДОБУТКУ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ У СУМУ

Та б л и ц я 20

1.Формули суми і різниці тригонометричних функцій

sin α+ sin β= 2 sin α+ β cos α− β			sin α− sin β= 2 sin	α− β cos α+ β
2		2		2	2

cos α+ cos β= 2 cos α+ β cos		α− β	cos α− cos β= −2 sin α+ β sin		α− β
2		2		2	2
tg α + tg β =	sin(α + β )		tg α− tg β=	sin(α − β)
tg α + tg β =	cos α cos β		tg α− tg β=	cos αcos β
	cos α cos β			cos αcos β

2. Перетворення добутку тригонометричних функцій у суму

sinα sin β= 12 (cos(α−β)−cos(α+β)) cosα cos β= 12 (cos(α−β)+cos(α+β)) sinα cos β= 12 (sin(α−β)+sin(α+β))

§ 7. Формули додавання та їх наслідки

Пояснення й обґрунтування

1. Формули суми і різниці тригонометричних функцій.

( За формулами додавання:

sin (x + y) = sin x cos y + cos x sin y; sin (x – y) = sin x cos y – cos x sin y.

Додаючи почленно ці рівності, одержуємо:

sin (x + y) + sin (x – y) = 2 sin x cos y. Якщо позначити:

х + у = α, х – у = β,

то, додаючи і віднімаючи рівності (2) і (3), маємо: x = α + β , y =

(1)

(2)

(3)

α− β . 2

Тоді з формули (1) одержуємо формулу перетворення суми синусів у добуток:

sinα+ sinβ= 2 sin	α+ βcos	α− β	.	(4)
	2	2

Словесно її можна сформулювати так:

Cума синусів двох аргументів дорівнює подвоєному добутку синуса півсуми цих аргументів на косинус їх піврізниці.

Якщо замінити у формулі (4) β на (–β) і врахувати непарність синуса: sin (–β) = –sin β, то одержимо формулу:

sinα− sin β= 2 sin	α − βcos	α + β	.
	2	2

	Різниця синусів двох аргументів дорівнює подвоєному добутку си
	нуса піврізниці цих аргументів на косинус їх півсуми.
Аналогічно, додаючи почленно рівності
	cos (x + y) = cos x cos y – sin x sin y,	(5)
	cos (x – y) = cos x cos y + sin x sin y,	(6)
одержуємо:
	cos (x + y) + cos (x – y) = 2 cos x cos y,	(7)
і, виконуючи заміни (2) і (3), маємо:

cos α+ cos β= 2 cos	α+ βcos	α− β	.
	2	2

	Сума косинусів двох аргументів дорівнює подвоєному добутку ко
	синуса півсуми цих аргументів на косинус їх піврізниці.
Якщо відняти рівності (5) і (6), то одержимо:
		cos(x + y)− cos(x − y) = −2 sinxsiny.				(8)

Тоді			cos α− cos β= −2 sin α+ βsin	α− β	.
			2	2

РОЗДІЛ 1. Тригонометричні функції

Різниця косинусів двох аргументів дорівнює: мінус подвоєний добу ток синуса півсуми цих аргументів на синус їх піврізниці.

Для обґрунтування формули перетворення суми (різниці) тангенсів досить використати означення тангенса і формули додавання:

tg α + tg β =

sinα

sinβ

sin α cosβ + cos α sinβ

sin(α + β)

cos α

cos β

cos α cos β

cos α cosβ

Отже,

tg α+ tg β=

sin (α+ β)

(9)

cos αcosβ

Якщо у формулі (9) замінити β на (–β) і врахувати непарність тангенса (tg (–β) = –tg β) і парність косинуса (cos (–β) = cos β), то одержуємо:

tg α − tg β =	sin(α − β )	.	(10)

	cos α cosβ

Зазначимо, що формули (9) і (10) справедливі тільки тоді, коли cos α ≠ 0

і cos β ≠ 0. )

2.Перетворення добутку тригонометричних функцій у суму.

(Зазначимо, що в процесі обґрунтування формул перетворення суми і різниці синусів і косинусів у добуток ми фактично отримали і формули перетво$ рення добутків тригонометричних функцій у суму. Дійсно, якщо поділити обидві частини рівності (1) на 2 і записати одержану рівність справа на$ ліво, маємо:

		sin x cos y = 1	(sin(x − y) + sin(x + y)) .		(11)
	2
Аналогічно, з формули (7) одержуємо:

		cos x cos y = 1	(cos(x − y) + cos(x + y))	,	(12)
		2
а з формули (8) (після ділення на –2), одержуємо:

		sin x sin y = 1 (cos(x − y) − cos(x + y)) .			(13)
2

Замінюючи у формулах (11–13) значення x на α, а y на β, одержуємо той запис цих формул, який наведено в таблиці 20. )

Приклади розв’язання завдань

Приклад 1 Перетворіть задану суму чи різницю в добуток і, якщо можли$ во, спростіть: 1) sin 75° + sin 15°; 2*) cos2 α – cos2 β.

Ко м е н т а р

1)У першому завданні можна безпосередньо застосувати формулу

sin α + sin β = 2 sin α + β cos α − β ,		а потім використати табличні значення
2	2

sin 45° і cos 30°.

§7. Формули додавання та їх наслідки

2)Якщо вираз cos2 α – cos2 β розглянути як різницю квадратів, то його можна розкласти на множники, а потім до кожного з одержаних виразів застосу$ вати формули перетворення різниці чи суми косинусів у добуток. Для по$ дальшого спрощення одержаного виразу використовуємо формулу синуса подвійного аргументу, а саме:

2 sin α + β cos α + β = sin(α + β ) і 2 sin α − β cos α − β = sin(α − β).

2	2	2	2
		Р о з в ’ я з а н н я

1) Xsin75° + sin15° = 2sin	75° + 15°	cos	75° − 15°	= 2sin45°cos30° = 2		2	3	=	6	. Y
	2		2			2	2		2

2) Xcos2 α − cos2 β = (cosα − cos β )(cosα + cos β)=
= −2 sin α + β sin α − β 2 cos α + β cos α − β = − sin(α + β)sin(α − β). Y
2	2		2		2

Приклад 2 Перетворіть у добуток sin α + cos β.

К о м е н т а р

Ми вміємо перетворювати в добуток суму синусів або косинусів. Для перехо$

ду до таких виразів досить згадати, що cosβ = sin(

2π − β)

(або sinα = cos(2π − α )).

Р о з в ’ я з а н н я

)

X sin α + cos β = sin α + sin(

− β)= 2 sin

α +

− β

α −

− β

cos

= 2 sin (α

2− β +

)cos (α

2+ β −

).Y

Приклад 3 Спростіть вираз (sin8α − sin2α )(cos2α − cos8α ). 1 − cos6α

К о м е н т а р Для спрощення заданого дробу можна спробувати скоротити його, а для

цього подамо чисельник і знаменник у вигляді добутків, які містять однакові вирази. У чисельнику використаємо формули перетворення різниці синусів і косинусів у добуток (а також непарність синуса: sin (–3α) = –sin 3α), а в зна$

меннику скористаємося формулою 1− cos x = 2 sin2 x .

			2
		Р о з в ’ я з а н н я
X	(sin8α − sin2α )(cos2α − cos8α )	=	2sin3α cos5α (−2)sin5α sin(−3α )	=
X	1 − cos6α	=	2sin2 3α

= 2 cos 5α sin 5α = sin10α .Y

РОЗДІЛ 1. Тригонометричні функції

	Доведіть тотожність 4sin70° −	1	= −2.
Приклад 4*
		sin10°

К о м е н т а р Доведемо, що ліва частина тотожності дорівнює правій. Після приведення

до спільного знаменника перетворимо добуток синусів на різницю косинусів,

а потім врахуємо, що cos 60° = 1 , а cos 80° = sin 10° (оскільки 80° + 10° = 90°).

Р о з в ’ я з а н н я

X 4 sin 70° −

Приклад 5*

(cos 60° − cos 80° ) − 1

4 sin 70° sin 10° −

sin 10°

− 2 cos 80° − 1

−2 cos 80°

−2 sin 10°

= −2. Y

sin 10°

Доведіть, якщо А, В, С — кути трикутника, то

sin A + sin B + sin C = 4 cos

cos

К о м е н т а р

Для кутів трикутника A + B + C = π. Тоді C = π – (A + B), і за формулами зведення sin (π – (A + B)) = sin (A + B). Після перетворення суми синусів sin A + sin B у добуток помічаємо, що аргумент (А + В) удвічі більший за

аргумент	A + B	. Це дозволяє записати sin (A + B) за формулою синуса по$
	2

двійного аргументу і в одержаній сумі винести за дужки 2 sin A + B , а потім

перетворити в дужках суму косинусів у добуток. Потім треба врахувати, що

A + B	=	π − C	=	π	−	C	і використати формули зведення.
2
	2		2		2

Р о з в ’ я з а н н я

X Враховуючи,щодлякутівтрикутникаC = π – (A + B), одержуємо sin A + sin B + sin C = sin A + sin B + sin (π – (A + B)) =

= 2 sin

A + B

cos

A − B

+ sin( A + B) = 2 sin

A + B

cos

A − B

+ 2 sin

A + B

cos

A + B

= 2 sin

A + B

(cos

A − B

+ cos

A + B

)= 2 sin

π − C

2 cos

cos

= 4 sin (

−

)cos

cos

= 4 cos

cos

. Y

§ 7. Формули додавання та їх наслідки

Запитання для контролю

1.Запишіть формули перетворення суми і різниці синусів або суми і різниці косинусів у добуток. Наведіть приклади використання цих формул.

2*. Запишіть формули перетворення суми і різниці тангенсів. Наведіть при$ клади використання цих формул.

3*. Доведіть формули перетворення суми і різниці тригонометричних функцій

у добуток.

4.Наведіть приклади використання формул:

sinxcosy =	1	(sin(x − y)+ sin(x + y));	cosxcosy =	1	(cos(x − y)+ cos(x + y));

2			2

sinxsiny = 1 (cos(x − y) − cos(x + y)).

5*. Доведіть формули, наведені в запитанні 4.

Вправи

1.Перетворіть суму (або різницю) тригонометричних функцій у добуток і спростіть:

1°) cos 152° + cos 28°;

2°) cos 48° – cos 12°;

3) cos 20° – sin 20°;

sin25

+ sin 15

;

5*) sin2 α – sin2 β;

6*) sin α + sin 2α + sin 3α + sin 4α;

sin25

− sin 15

7*) cos α + cos 2α + cos 3α + cos 4α.

2. Доведіть тотожність:

sin 75

+ sin 15

sin α + sinβ

α+β

;

cos6α − cos10α

= 2 sin 2α;

1°) cos 75 − cos 15 = −

2°) cos α + cosβ

sin8α

		sinα + sinβ			cos α − β
4)		sinα + sinβ		=			2	;
4)	sinα cos β + cos α sin β			=	cos		α + β	;
	sinα cos β + cos α sin β						α + β
							2
							2
6*)		sinα − cos β	= tg(α − β −			π	);
6*)		cos α − sin β	= tg(α − β −				);
		cos α − sin β	2		4

3. Перетворіть у суму:

7*)

(sin2α + sin6α )(cos2α − cos6α )			= sin4α;

	1 − cos 8α
	sin α + sin3α + sin5α + sin7α	= ctg2α.
	cos α − cos 3α + cos5α − cos7α

1) cos 45° cos 15°; 2) sin

cos

5π

;

3) sin 20° sin 10°; 4)

cos

cos π .

4. Обчисліть:

1) 2 cos 20°æcos 40° – cos 20°;

2*) 4 sin 10°æsin 50°æsin 70°.

5*) Доведіть, що при α + β + γ = π виконуються рівності:

sin α − sin β + sinγ = 4 sin α cos β sin

;

cosα + cosβ + cosγ = 1+ 4 sin α sin β sin

§8	ГРАФІКИ РІВНЯНЬ ТА НЕРІВНОСТЕЙ
	З ДВОМА ЗМІННИМИ

Т а б л и ц я 21

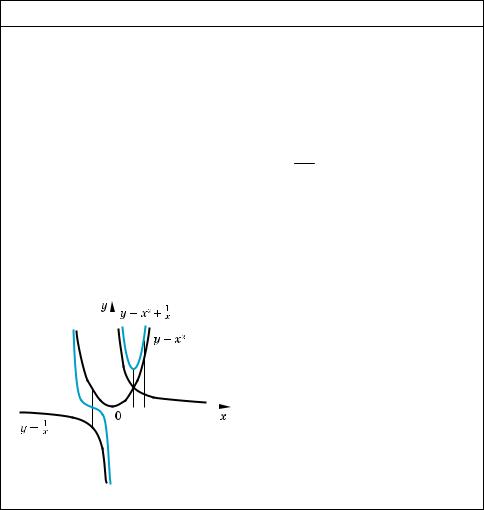
1. Побудова графіків функцій виду y = f (x) + g (x)

Якщо нам відомі графіки функцій y = f (x) та y = g (x), то ескіз графіка функції y = f (x) + g (x) можна побудувати так: зобразити в одній сис% темі координат графіки функцій f (x) і g (x), а потім будувати шуканий графік за точками, виконуючи для кожного значення x (з області визна% чення функції f (x) + g (x)) необхідні операції над відрізками, які зобража% ють відповідні ординати f (x) і g (x).

Аналогічно можна будувати і схематичні графіки функцій y = f (x)æg (x) та y = f(1x).

Приклад

Коментар

Побудуйте графік функції

Будуємо в одній системі коорди$

y = x2 +

нат графіки функцій$доданків:

y = x2 та y =

(на рисунку побудо$

вані штриховими лініями). Для

кожного значення x (крім x = 0, яке

не входить до області визначення

заданої функції) додаємо відповідні

відрізки — значення функцій (спра$

ва від осі Оy) або віднімаємо, якщо

значення f (x) і g (x) протилежні за

знаком (у даному випадку – зліва

від осі Оy). На рисунку синьою

лінією зображено результат — гра$

фік функції y = x2 +

100

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 4510 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.03.20158.49 Mб8978-966-00-1063-5.pdf
#
07.03.2016315.39 Кб16ADMINISTRATIVNO_PRAVOVIJ_STATUS_MON-2.doc
#
07.03.2016359.42 Кб12AGRARNA_POLITIKA_UTsR_DIPLOMNA_ROBOTA.doc
#
21.11.2019178.18 Кб5Alekhina_glava4-97.doc
#
09.11.20194.5 Mб23Alesinskaya_Reshenie_zadach_Ekonom_metody_model...doc
#
22.03.20155.24 Mб69algebra10_нелін_дворівн.pdf
#
26.12.2019281.09 Кб0Alkemy_RU.doc
#
07.03.20161.34 Mб231AMMA.doc
#
12.11.20181.63 Mб27Angl.doc
#
30.04.201517.56 Кб46angl.docx
#
22.03.201533.28 Кб316Annotatsia_proizvedenia_Groza.doc