
OFP-Tretyak-Lozovski
.pdf
ОСНОВИ ФІЗИКИ НАПІВПРОВІДНИКІВ |
198 |
во-розмірних систем залежать від щільності станів на рівні Фермі N(EF ). Таким чином, для квантових ям стрибкоподібна поведінка
N(EF ) за зміни товщини ями L приводить до осцилюючої залежності
від L питомого опору, константи Холла та магнетопровідності. Крім того, виникають особливості в тунельних характеристиках тонких металічних плівок (напр. такі, що спостерігались у плівках Pb, Mg, Au, Ag). Дійсно, тунелювання електронів наводить безпосередні докази існування рівнів розмірного квантування у шаруватих системах із надтонкими шарами. Відомо, що ймовірність тунелювання електронів через бар'єр визначається параметрами, що характеризують бар'єр, і щільністю початкових і кінцевих станів. Таким чином, у тонкоплівковій системі метал–діелектрик–метал особливості щільності станів ви-
значатимуть особливості тунельного струму IT від напруги U. Най-
більш цікавими з поглядупрактичних застосувань є квантово-розмірні ефекти у напівпровідникових гетероструктурах. Наприклад, у гете-
роструктурах із квантовими ямами AlxGa1-xAs-GaAs-AlxGa1–xAs рух електронів обмежено шарами GaAs, а шари AlxGa1–xAs відіграють роль потенціальних бар'єрів. Якщо товщина бар'єрних шарів не дуже мала, то гетероструктуру можна розглядати як набір не пов'язаних між собою плівок GaAs. При цьому, якщо товщина плівок становить величину
10–7-10–6 см, то розмірне квантування спричинить ефективну модифікацію енергетичних станів структури, що істотно змінює, наприклад їхні оптичні властивості. Розмірне квантування зумовлює зсув дна
зони провідності EC в арсеніді галію на величину E1(k = 0) . Це пр и-
водить до ефективного збільшення ширини забороненої зони, що викликає зсув червоної межі смуги поглинання у жовтий бік залежно від товщини квантової ями. Квантово-розмірні явища спостерігаються для тонких шарів GaAs – завтовшки порядку десятків нанометрів. Піки у спектрі поглинання зумовлені переходами електронів із заповненої n-ї підзони у валентній зоні до порожньої n-ї підзони у зоні провідності. Аналогічні особливості спостерігаються й в спектрах люмінесценції.
Залежність оптичних властивостей систем із квантовими ямами від їхньої товщини використовується для створення лазерів із вдосконаленими характеристиками. Зокрема, у таких лазерах спостерігається короткохвильовий зсув частот випромінювання, зниження порогової потужності накачування тощо.
Слід зазначити, що квантово-розмірні ефекти спостерігаються лише у досконалих та однорідних за товщиною плівках. Кількісно це означає, що поширення ліній рівнів δЕ розмірного квантування через розсію-
199 |
|
Розділ 16. Низьковимірні напівпровідникові системи |
||||||
вання носіїв заряду на домішках, фононах і шорсткостях поверхні |
||||||||
плівки має бути малим щодо відстані між енергетичними рівнями |
||||||||
розмірного квантування ∆Е. При цьому флуктуації товщини плівки |
||||||||
мають бути меншими за довжину хвилі електрона на рівні Фермі λF . |
||||||||
Осциляції, обумовлені квантово-розмірними ефектами, найбільш яс- |
||||||||
краво виявляються у тонких плівках, де L ~ λF |
за низьких температур |
|||||||
коли температурне розмиття щільності станів N(E) є меншим за ∆Е |
||||||||
(kT << ∆E ). Таким вимогам до систем краще за все відповідають епі- |
||||||||
таксіальні шари (типу шарів GaAs у багатошарових гетероструктурах), |
||||||||
а також плівки напівметалів (Bi, Sn, Sb та їхні сплави) і вироджених |
||||||||
напівпровідників із вузькою забороненою зоною (InSb, PbTe) в інтер- |
||||||||
валах товщин L ~103 – 104 нм. У металічних плівках через малі зна- |
||||||||
чення λF |
вимогу однорідності плівки за товщиною досить важко ви- |
|||||||
конати. |
|
|
|
|
|
|
EC(2) |
|
Крім плівок і гетероструктур, |
(1) |
|||||||
квазідвовимірний |
електронний |
EC |
|
|||||
газ можна отримати й поблизу |
EF |
(2) |
||||||
меж розподілу на контактах між |
|
EV |
||||||
двома напівпровідниками в ін- |
квазідвовимірний |
|||||||
електронний газ |
||||||||
версних |
і |
збагачених |
шарах |
|
GaAs |
|||
МДН-структур і модуляційно-ле- |
E(1) |
|||||||
|
||||||||
гованих гетероструктурах. Ва- |
V |
|
||||||
жливою перевагою цих |
систем |
Ga1–x Alx As |
||||||
над плівковими |
є |
можливість |
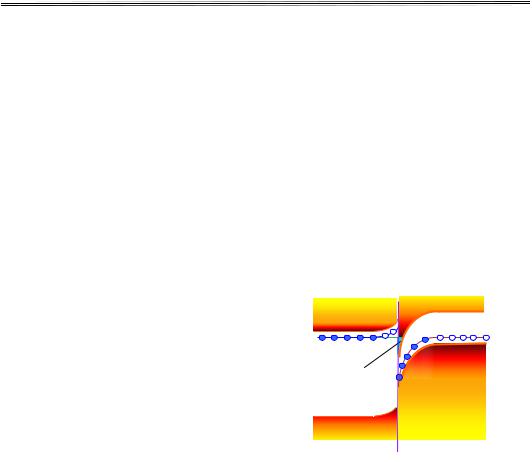
Рис. 16.2. Утворення каналу |
|||||
керованої |
|
зміни |
концентрації |
|||||
носіїв у широких межах. Моду- |
квазідвовимірних електронів на межі |
|||||||
розподілу модуляційно-легованої |
||||||||
ляційно-леговані гетерострук- |
||||||||
гетероструктури. |
||||||||
тури, які складаються із перехо- |
Синіми кульками позначено домішкові рівні, |
|||||||
дів GaAs-AlGaAs (рис. 16.2), виро- |
заповнені електронами, білими – дірки. |
|||||||
Рівень Фермі збігається із рівнем донорної до- |
||||||||
щуються |
|
зазвичай |
методами |
|
мішки в AlGaAs |
|||
молекулярно-променевої епітак- |
|
|||||||
|
|
|||||||
сії. При |
|
|
|
|
|
|
|
|
цьому шар або частина шару AlGaAs легується (концентрація донорів |
||||||||
~ 1018 cм–3 ), а шар GaAs не легуєтьсяабо слабко легується акцепторами. |
||||||||
Таке легування спричиняє викривлення зон, оскільки електрони, на- |
||||||||
магаючись встановити єдине значення рівня Фермі в системі, пере- |
||||||||
ходять із донорів до потенціальної ями, що утворюється вигином зон, з |
||||||||
одного боку, і розривом дна зони провідності на гетеропереході – з |
||||||||
іншого. Такі електрони можуть вільно рухатись тільки вздовж границі |
||||||||
гетеропереходу. Квантування поперечного руху в ямі (аналог розмір- |
||||||||

ОСНОВИ ФІЗИКИ НАПІВПРОВІДНИКІВ |
200 |
ного квантування у плівці) приводить до виникнення квазідвовимір-
ного електронного газу із поверхневою концентрацією 1011–1012 cм–2. У такій системі поверхневі стани та дефекти (з авдяки відповідності ґраток GaAs та AlGaAs) не впливають суттєво на формування фізичних властивостей. З іншого боку, розсіювання електронів на домішках, що їх породили, також незначне через їхнє просторове розділення. За рахунок цього досягаються високі значення рухливості електронів. Наприклад, за температури 4К рухливість електронів може досягати
величин µ = 106 cм2/Вс, за температури 77К – µ = 105 cм2/Вс, і за 300К
– µ = 104 cм2/Вс. Завдяки таким високим значенням рухливостей польові транзистори, створені на модуляційно-легованих гетероструктурах із квазідвовимірним електронним газом, характеризуються великою швидкодією ≥10 пс в інтервалі температур 77–300 К. Останнім часом все більшу увагу як дослідники, так і практики приділяють системам із квантовими точками (системи, в яких квантово-розмірні об'єкти обмежені у просторі вздовж всіх трьох осей). У таких системах електронні стани кантуються, подібно станам у тривимірному потенціальному ящику.
Специфіка фізичних ефектів у низьковимірних системах, що не пов'язана із просторовим квантуванням, полягає, як зазначалось вище, у наявності меж розподілу. Такі (класичні розмірні ефекти) можуть спостерігатись у тонких плівках і малих частинках. Історично першим класичним ефектом, що пов'язаний із пониженою розмірністю системи, було визначення залежності провідності тонких плівок металів і сильно легованих напівпровідників від товщини плівки. Виявилось, що додаткове розсіювання носіїв границями плівки спричиняє зменшення провідності тонких плівок. Вплив розмірів зразка (товщини плівки) на його електропровідність стає помітним, коли ці розміри стають порівняними із довжиною вільного пробігу електрона. Таким чином, розмірні ефекти різкіше виражені у чистих монокристалічних плівках, оскільки довжина вільного пробігу в них істотно перевищує таку довжину у розупорядкованих із великою кількістю домішок зразках. До класичних розмірних ефектів можна зарахувати також можливість збудження поверхневої хвилі (поверхневого поляритону або плазмон-поляритону) p- та s-поляризації, якщо поверхня, де збуджується хвиля, вкрита дуже тонкою плівкою іншого матеріалу. Оскільки ці ефекти походять від наявності поверхні, де локальні поля дуже неоднорідні, то зрозуміло, що головним чином вони пов'язані з нелокальними електродинамічними взаємодіями. А оскільки такі ефекти р о- зігруються на відстанях, що порівняні із товщиною перехідного шару поблизу поверхні, які в свою чергу є набагато меншими за довжину
201 |
Розділ 16. Низьковимірні напівпровідникові системи |
хвилі зовнішнього випромінювання (якщо йдеться про оптичні властивості), то доводиться мати справу зі специфічними розподілами електромагнітного поля, коли не можна говорити про довжину хвилі, оскільки на таких відстанях фронт хвилі ще не може сформуватись. У такому випадку кажуть, що фізичні ефекти розігруються у ближньому полі. Розвиток сучасних експериментальних методів вивчення властивостей мезооб'єктів (таких, лінійні розміри яких досить малі для того, щоб ефекти нелокальності та неоднорідності поля відігравали суттєву роль, а з іншого боку ці розміри досить великі для того, щоб об'єкти ще можна було описувати в класичному наближенні) спричинив виникнення цілої нової галузі фізики – фізики ближнього поля.
16.2. Електронні фундаментальні довжини |
|
||||||||||
Як ми обговорювали у попередніх розділах, електрон у напівпрові- |
|||||||||||
днику характеризується ефективною масою m*, яка зазвичай менша за |
|||||||||||
масу вільного електрона. Таким чином довжина хвилі де Бройля в на- |
|||||||||||
півпровіднику є більшою за довжину хвилі де Бройля вільного елек т- |
|||||||||||
рона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λB = |
h |
= |
h |
0 |
m |
|
(16.9) |
|
|
|
|
p |
|
= λB |
m* |
|
||||
|
|
|
|
|
|
2m*E |
|
|
|||
Відомо, що відношення ефективних мас електронів для InSb |
|||||||||||
m*/m = 0.014, для GaAs – m*/m = 0.067, для GaN – m*/m = 0.172, для SiC |
|||||||||||
– m*/m = 0.41. Тоді із (16.9) маємо абсолютні значення довжин хвиль де |
|||||||||||
Бройля |
для |
цих |
напівпровідників |
|
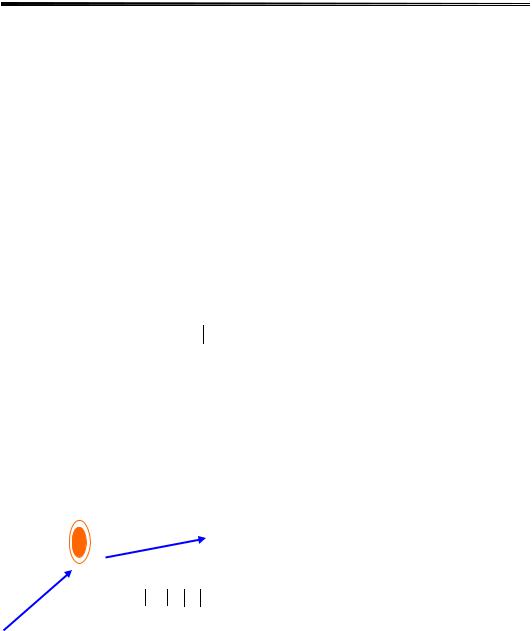
λB (нм) |
|
|
|
|||
(рис. 16.3). Зясуємо, за яких розмірів |
|
|
|
|
|||||||
системи |
можна |
очікувати |
ефекти |
|
|
|
|
|
|||
розмірного (просторового) кванту- |
|
|
|
|
|
||||||
вання. |
Нехай |
геометричні |
розміри |
|
60 |
InSb |
|
|
|||
напівпровідникового зразка |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
Lx × Ly × Lz. |
|
|
|
|
40 |
|
|
|
||
Припустимо, що Lx < Ly < Lz. Якщо си- |
|
GaAs |
|
||||||||
|
|
|
|||||||||
стема, що розглядається, є однорід- |
|
|
|
GaN |
|
||||||
ною, а процеси розсіювання електро- |
|
20 |
|
|
|||||||
нів є слабкими, то можна вважати рух |
|
|
|
SiC |
|
||||||
|
|
|
|
|
|||||||
електронів у такому зразку квазіба- |
|
|
|
|
m*/m |
||||||
лістичним, і тільки лінійні розміри си- |
|
10 |
10–1 |
100 |
|||||||
стеми необхідно порівнювати із дов- |
Рис. 16.3. Довжини хвиль електронів |
||||||||||
жиною |
хвилі |
де |
Бройля. |
Оскільки |
|
у напівпровідниках при Т=300 К |
|||||
|
|
|
|
|
|
|
|
залежно від ефективної маси |
|||

ОСНОВИ ФІЗИКИ НАПІВПРОВІДНИКІВ |
204 |
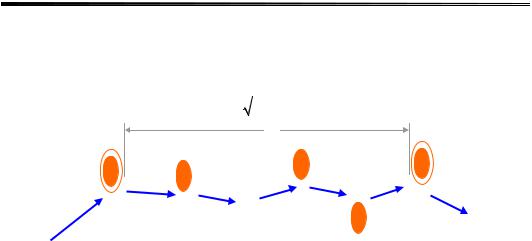
електрон багато разів розсіюється перед тим, як його енергія помітно зменшується (рис. 16.6). У результаті його рух є хаотичним, і середнє
переміщення його за час τE визначається коефіцієнтом дифузії D
LE = |
DτE |
, (τE >> τe ) |
(16.18) |
LE
 le
le 

Рис. 16.6. Стохастизація руху електрона за пружного та непружного розсіювання
Коефіцієнт дифузії можна подати формулою
|
v2τ |
|
D = |
αe , |
(16.19) |
де параметр α = 3 для тривимірного електронного газу, α = 2 – для двовимірного і α =1 – для одновимірного.
За збільшення температури число електронів, що можуть брати участь у транспорті, збільшується та все більша кількість електронів із різною енергією можуть брати участь у кінетичних процесах. Когерентність у системі при цьому порушується через широкий розподіл фаз
хвильових функцій. Дійсно, нехай kBT << EF . Тоді кожен електронний
стан має майже однакову амплітуду, але трохи різні фази. Поки ця різниця є малою, усереднення за електронними станами всередині температурно-розмитої функції розподілу електронів не порушує їхню фазу і, тим самим, зберігає когерентність електронів. Але за збільшення температури, коли електрони з істотно різними енергіями беруть участь у кінетичних процесах, когерентність у системі порушується, оскільки усереднення за станами відбувається із значно розмитою функцією розподілу електронів. Нехай LT – характерна довжина, на якій порушується когерентність електронів завдяки ненульовій температурі. Температурне розмиття функції розподілу пропорційне
kBT і призводить до того, що розмиття фаз змінюється з часом як t (kBT / ) . Таким чином, для оцінки часу розмиття фаз можна вик о- ристати величину

205 |
Розділ 16. Низьковимірні напівпровідникові системи |
|||
|
τT = |
|
. |
(16.20) |
|
|
|||
|
|
kBT |
|
|
Якщо процеси розсіювання є пружними, то електрон дифундує в
просторі на відстань 
 Dt за час t, що перевищує середній час віль-
Dt за час t, що перевищує середній час віль-
ного пробігу τе. Таким чином, протягом часового інтервалу τТ електрон продифундує завдяки термічному руху на довжину
LT = |
DτT |
= |
D /kBT |
. |
(16.21) |
Отже когерентність електронів порушується на відстанях, що перевершують довжину LT.
Зрозуміло, що ефекти дефазування, викликані непружним розсіюванням і температурним розмиванням функції розподілу, діють одночасно. Тоді просторовий масштаб, пов'язаний із втратою кванто- во-механічної когерентності, можна визначити як меншу з двох дов-
жин LE та LT
lφ min{LE ,LT } . |
(16.22) |
Оскільки електронний транспорт визначається суперпозицією електронних хвильових функцій, із вищенаведеного розгляду можна
зробити висновок, що довжина когерентності lφ визначає просторовий розмір, нижче якого електронний транспорт має квантовий характер.
Можна також розглянути нерівноважну біполярну систему, що містить як електрони, так і дірки. Тоді, якщо τR – час життя носіїв у си-
стемі, то довжина LR = 
 DτR визначатиме середню відстань, на якій
DτR визначатиме середню відстань, на якій
нерівноважні носії дифундують, перед тим як рекомбінувати.
Таким чином, прилади, геометричні розміри яких становлять порядок довжини когерентності, не можна описувати макроскопічними матеріальними параметрами – провідністю, дрейфовою швидкістю тощо. Такі прилади необхідно описувати в рамках квантової теорії. З
іншого боку, для приладів, в яких транспортні відстані Ltr є більшими
порівняно із довжиною когерентності lφ можна описувати в рамках класичної фізики.
Розглянемо тепер умови реалізації квантового та класичного режимів електронного транспорту. Для цього припустимо, що транспорт відбувається вздовж однієї вісі, тобто повний струм уздовж інших двох осей, є нульовим. Але поперечні розміри приладу (вздовж осей) можуть відігравати важливу роль. Можна визначити кілька принципово різних типів транспорту електронів у просторово обмежених системах.
Почнемо із квантового та мезорежимів транспорту. Якщо довжина хвилі де Бройля перевищує лінійні розміри приладу Lz

ОСНОВИ ФІЗИКИ НАПІВПРОВІДНИКІВ |
206 |
λB ≥ Lz , |
(16.23) |
і крім цього, виконується нерівність |
|
le >>λB, |
(16.24) |
то маємо квантово-балістичний режим електронного транспорту. Випадок, коли
lφ > Lz, λB |
(16.25) |
відповідає мезорежиму електронного транспорту. Таким чином, можна стверджувати, що поперечні (до вісі ОZ) розміри приладу визначають одно-, двота тривимірний характери квантово-балістичного та мезорежимів електронного транспорту.
Класичний режим електронного транспорту реалізується у випад-
ку, якщо виконується нерівність
Lz > lφ. |
(16.26) |
Якщо лінійний розмір приладу вздовж вісі OZ при цьому є меншим за довжину вільного пробігу електрона, то відбувається класичний балістичний режим електронного транспорту. Іншими словами, у цьому випадку електрони можуть рухатись уздовж приладу за класичними траєкторіями без зіткнень. Якщо
Lz >> lφ, |
(16.27) |
то електронний транспорт має дифузійну природу. У випадку, коли виконуються співвідношення
Lz ~ lE >> le, |
(16.28) |
електрони не втрачають енергію, рухаючись уздовж приладу. Тоді кажуть про реалізацію квазібалістичного режиму електронного транспорту. Зрозуміло, що можуть реалізуватись три класичних режими електронного транспорту для одно-, двота тривимірних рухів елект-
ронів. Якщо обидва поперечні розміри приладу Lx та Ly набагато більші за довжину хвилі де Бройля, але порівняні із характеристичними класичними довжинами, спостерігатимуться поперечні класичні розмірні ефекти в електронному транспорті. У цьому випадку зіткнення електронів із поперечними поверхнями приладу визначатимуть транспорт вздовж вісі OZ. Наприклад, якщо один із двох поперечних розмірів приладу має порядок довжини вільного пробігу електронів
Lx ,Ly ~le , опір приладу вздовж вісі OZ залежатиме від його бічних меж.
Якщо поперечні розміри приладу стають порівняними з однією із дифузійних довжин, ми отримаємо інший тип класичних розмірних
ефектів. Наприклад, якщо Lx або Ly мають порядок довжини релаксації енергії LЕ, границі приладу забезпечують додатковий канал ре-

207 Розділ 16. Низьковимірні напівпровідникові системи
лаксації енергії. Такий дифузійно-розмірний ефект визначає середню енергію нерівноважних електронів.
На останок зведемо ієрархію довжин електронного транспорту до таблиці
|
|
|
|
|
|
|
|
|
|
|
Таблиця 16.1 |
|
|
Квантовий |
|
Міжконтактна |
відстань |
Lz є порівняною із |
|||||||
|
режим |
|
довжиною хвилі електрона Lz ~ λВ |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Міжконтактна відстань Lz є меншою за дов- |
|||||||||
|
Мезорежим |
|
жину, на якій відбувається дефазування хви- |
|||||||||
|
|
|
льової функції електронів Lz ≤ lφ |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Міжконтактна |
відстань |
Lz перевищує дов- |
|||||||
) |
|
жину, на якій відбувається дефазування хви- |
||||||||||
|
Класичний режим (одно-, двоабо тривимірний електронний транспорт |
|
льової функції електронів Lz > lφ |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
квазібалістичний режим |
|
|
|
поперечні розмірні |
|||
|
|
|
балістичний режим: |
|
(енергія зберігається): |
φ |
|
ефекти |
||||
|
|
класичний |
|
, l |
|
|
|
R |
||||
|
|
|
e |
|
|
|
||||||
|
|
z |
≥l |
|
e |
|
,L |
|||||
|
|
≥L |
z |
|
~l |
|
E |
|||||
|
|
e |
L |
|
y |
|
~L |
|||||
|
|
|
≥ |
|
,L |
|
y |
|||||
|
|
|
E |
|
x |
|
L |
|||||
|
|
l |
L |
|
середньої довжини прбігувільного: L |
|
, |
|||||
|
|
|
|
x |
||||||||
|
|
|
|
дифузійні: L |
||||||||
16.3. Гетероструктури. Квантові ями, квантові голки, квантові точки
Гетероструктура формується, коли два різних матеріали з'єднуються
водну структуру із межею розподілу між ними. Умови формування гетероструктур і різні типи гетерограниць ми розглядали у розд. 13. Скористаємось цими відомостями та розглядатимемо гетероструктури,
вяких може спостерігатись просторове кантування. Найпростішими та найпоширенішими подбіними гетерострукутрами є квантові ями. Властивостям квантових ям, а також квазіодновимірних – квантових голок і квазінульвимірних – квантових точок – об'єктів й буде присвячено обговорення у цьому розділі.
Сучасні технології дозволяють виготовляти ці межі розподілу майже ідеальними. Наприклад, перехідний шар, що утворюється на межі
розподілу завдяки досягненням сучасних технологій (базуються на
