
OFP-Tretyak-Lozovski
.pdf


ОСНОВИ ФІЗИКИ НАПІВПРОВІДНИКІВ |
282 |
V |
V |
a |
|
|
B |
r |
N(E) |
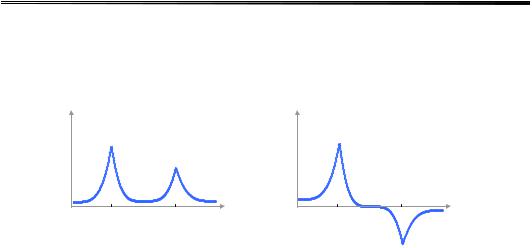
Рис. 17.3. Потенціальна енергія та щільність станів у регулярній структурі |
|
Припустимо тепер, що ями розташовані досить далеко одна від одної так, що перекриття між атомними хвильовими функціями φ(r) на су-
сідніх вузлах є незначним. Нехай Rn – координата n-ї ями. То ді блохівську хвильову функцію електрона у кристалі можна записати як
ψ (x,y,z) = ∑eik Rn φ(r − R |
n |
) |
. |
(17.13) |
k |
|
|||
n |
|
|
|
|
Функції φ вважатимемо сферично-симетричними. Якщо тепер W0 –
енергія рівня в ізольованій ямі, то енергії електрона у простій кубічній ґратці, що відповідають хвильовим функціям (17.13) ,
E =W0 +Wk , |
(17.14) |
|
з |
|
|
Wk |
= −2I ∑ coskja , |
(17.15) |
|
j =x,y,z |
|
де інтеграл перекриття |
|
|
I = ∫drφ*(r − Rn )Hφ(r − Rn +1), |
(17.16) |
|
H – гамільтоніан системи. Інтеграл перекриття залежить від вигляду потенціалу, що формує ями і майже завжди може бути представлений у вигляді
I = I0e−αR . |
(17.17) |
При цьому параметр α визначається таким чином, що exp(−αr ) дає швидкість спадання хвильової функції ізольованої ями із відстанню
α = |
|
2mW |
0 |
|
. |
(17.18) |
2 |
|
|||||
|
|
|
|
|
|
|
Для воднеподібних атомних хвильових функцій оцінка передекспоненційного фактора I0 дає



287 |
Розділ 17. Невпорядковані напівпровідникові структури |
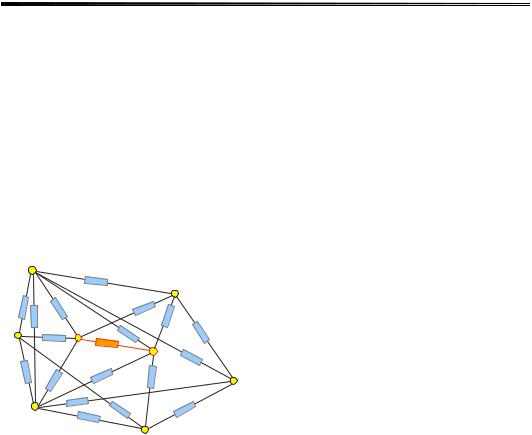
іншої). Важливим аспектом концепції стрибкової провідності є припущення, що всі центри локалізації характеризуються різними енергіями, тобто два центри з однаковою енергією локалізації розташовані на нескінченній відстані один від одного. Оскільки одним із прикладів невпорядкованих систем є домішкові напівпровідники, характерні властивості стрибкової провідності розглянемо, виходячи із моделі домішкової зони за слабкого легування.
Нехай домішкові центри характеризуються координатами ri , а хвильові функції локалізованих на них електронів затухають на нескінченності згідно із моделлю воднеподібної домішки
|
|
ε 2 |
|
−3/2 |
e−|r−ri|/aB |
|
|
|
ψ(r − r ) |
|
|
|
|
, |
(17.27) |
||
* |
|
|
||||||
i |
|
e |
2 |
|
||||
|
m |
|
|
|
|
|
||
де введено перенормований борівський радіус зонного електрона aB = ε 2 m*e2 із діелектричною проникністю напівпровідника ε та ефективною масою m* 1 . За невеликої концентрації домішок N (aB3 N <<1) домішкові стани можна вважати локалізованими. Але за-
m*e2 із діелектричною проникністю напівпровідника ε та ефективною масою m* 1 . За невеликої концентрації домішок N (aB3 N <<1) домішкові стани можна вважати локалізованими. Але за-
вдяки експоненційним хвостам хвильових функцій перекривання хвильових функцій сусідніх центрів є помітним, і за мірою цього перекривання існує ймовірність переходу (стрибка) електрона з одного центра на інший
1 |
F(ϕij , fi , f j )∫d3q|Mq |2 δ( qs − ∆ij ), |
(17.28) |
|
||
τij |
|
|
У цій формулі s – швидкість звука, а δ-функція забезпечує закон збереження енергії і відбирає фонони, що випромінюються або погли-
наються електроном, для компенсування різниці енергій ∆ij = εi − εj
початкового j та кінцевого i станів. Функція F описує статистичні умови переходу з j-го до i-го станів і пропорційна ймовірності того, що початковий стан заповнений, а кінцевий – незаповнений, тобто добутку функції розподілу Фермі початкового стану
|
|
−1 |
і кінцевого стану |
(1− fi ), |
а також залежить |
||||||
f j = exp(εj − µ)/kT +1 |
|
||||||||||
від функції розподілу фононів за енергіями |
∆ |
ij |
: |
ϕ |
= |
exp(∆ |
ij |
/kT )−1 −1 . |
|||
|
|
|
|
|
|
ij |
|
|
|
||
Для якісних висновків можна користуватись оцінкою цієї функції
1 Зрозуміло, що ефективну масу можна ввести лише для кристалічного напівпровідника. Введення ефективної маси у (17.27) означає, що розглядається кристалічний стан напівпровідника із достатньо великою концентрацією домішкових центрів, але такою, що дозволяє розглядати систему як кристалічну.



 ...
...
 x
x
 x
x