Функция нескольких переменных (ошибки косвенных измерений)

Часто встречаются случаи, когда искомая функция зависит от нескольких величин, каждая из которых определяется с ошибкой. Например, объем цилиндра зависит как от радиуса r (или диаметра d), так и от высоты h:

.

Общую функциональную зависимость в этом случае можно представить в виде ЕслиА и В являются отклонениями измеренных значений от истинных параметров, то степень зависимости Z от них будет также обусловлена частными производными

В этом случае для каждой серии измерений

или .

При этом мы можем указать знак отклонения в большую или меньшую сторону) для А и В. Для данной серии может получиться, что знаки ошибок противоположны и скомпенсируют друг друга, однако это не говорит о большой точности измерения.

Чтобы избежать зависимости от знака ошибки при усреднении по всем сериям, пользуются следующим способом. Возведем в квадрат выражение для Z:

.

Затем, усреднив по сериям и учитывая, что в связи со случайным, но равновероятным появлением знаков (+) и (–) у А и В , получим

.

Пример. Найдем ошибку в определении объема цилиндра. Сначала определим частные производные:

.

Абсолютная погрешность в определении объема будет:

.

Если Z - функция произвольного числа аргументов, т. е. Z= Z(A,B,D,E....), то среднеквадратичная ошибка среднего , которую мы здесь обозначим какZ, будет равна:

.

Пользуясь обозначениями дифференциального исчисления, погрешность величины у, представляющей собой функцию от переменных х₁, х₂, …, х_n: у=f(х₁, х₂, …, х_n ), можно записать в виде

,

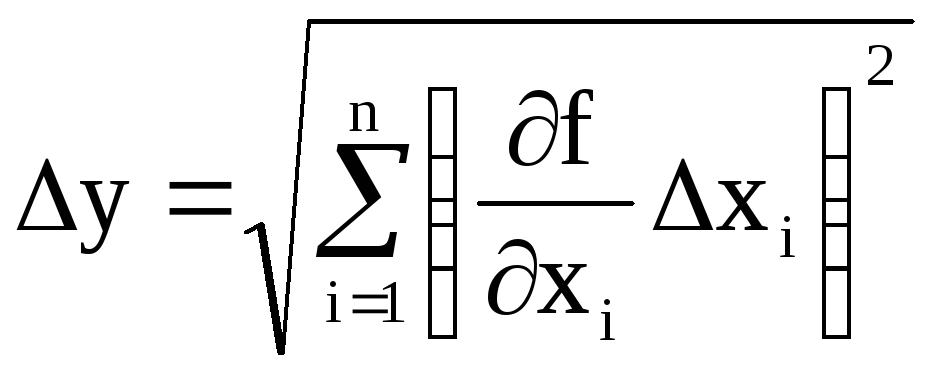где х₁, х₂, …, х_n - абсолютные погрешности х₁, х₂, …, х_n соответственно, f/x₁, f/x₂, …, f/x_n – частные производные у по переменным х₁, х₂, …, х_n соответственно. Частная производная функции многих переменных f(х₁, х₂,…, х_n) по одной переменной, допустим х₁, является обычной производной функции f по х₁, причем, другие переменные х₂, …, х_n считаются постоянными величинами. Все производные вычисляются при значениях х₁ = х_1ср, х₂ = х_2ср, …, х_n = х_nср.

Относительную погрешность величины у можно вычислить согласно формуле:

.

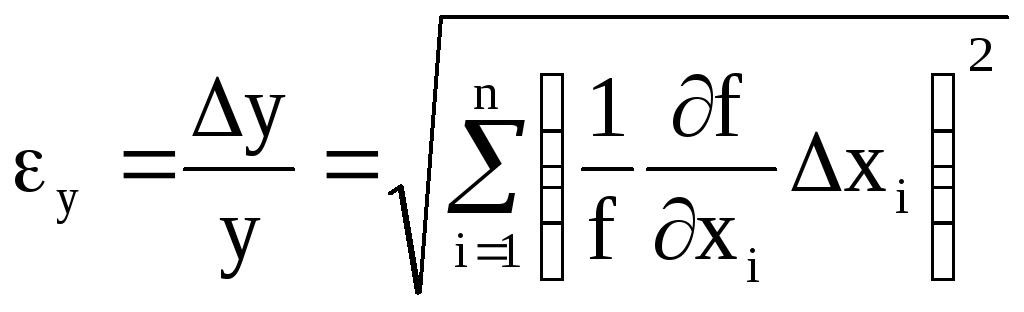Поскольку , то для относительной погрешности получаем

.

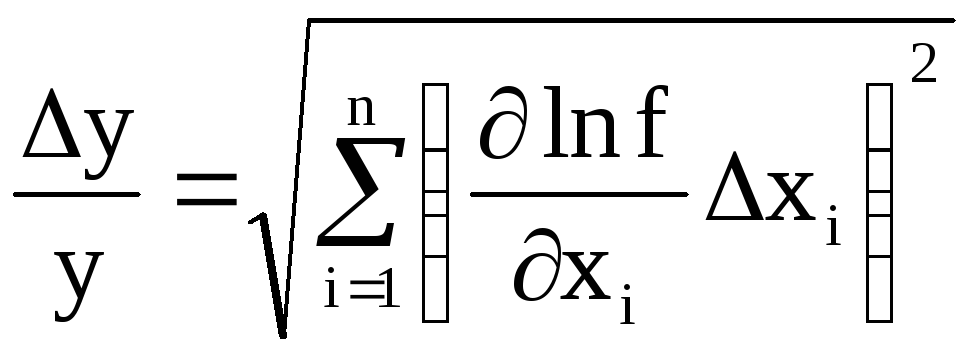Рассмотрим в качестве примера функцию трех переменных u = x^y^/z^, где , ,  – любые рациональные числа, тогда относительную погрешность измерения величины u можно рассчитать по формуле:

_u = ( ²_x ² + ²_y ² + ²_z ²)^1/2,

где _x, _y, _z - относительные ошибки измерений величин x, y, z.

При невысокой точности измерительных приборов случайными ошибками обычно можно пренебречь по сравнению с погрешностью измерительного прибора. Для получения результата достаточно одного отсчета.

Пусть Z = f(A, B, D, …), где A, B, D, …– непосредственно измеряемые величины, а A, B, D, … – их абсолютные систематические ошибки, тогда можно предложить следующий алгоритм нахождения абсолютной ошибки косвенных измерений:

1. Продифференцируем формулу исследуемой величины:

.

2. Знаки дифференциалов “d” заменяем знаками погрешностей “”, в случае получения в реальной формуле знаков “–” у каких-либо частных производных заменяем их на знаки “+”:

В некоторых случаях сначала удобнее находить относительную ошибку и уже затем абсолютную.

Пусть функциональная зависимость имеет вид: .

1. Прологарифмируем исходную формулу:

.

2. Продифференцируем полученную в результате логарифмирования формулу:

.

3. Знаки дифференциалов “d” заменяем знаками погрешностей “”, в случае получения в реальной формуле знаков “–” у каких-либо частных производных заменяем их на знаки “+”:

.